
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторить упражнение без подсказок с новыми точками.Содержание книги
Поиск на нашем сайте
6. Закрыть программу, не сохраняя проект: - навести курсор на кнопку - в окне, которое появилось, нажать кнопку Нет. Памятка: Для того чтобы отказаться от избранной функции кнопки, необходимо нажать правую кнопку.
Построение отрезка из точки до точки пересечения с прямой (отрезком) под определенным углом к ней (нему) Чтобы построить отрезок из точки до точки пересечения с прямой (отрезком) под углом к ней, нужно: • выбрать закладку „ Линии” (если она еще не выбрана) - навести курсор на соответствующую закладку, нажать левую кнопку мыши; • нажать кнопку • перекрестие курсора навести на точку (1), из которой построим линию, нажать левую кнопку мыши; • перекрестие курсора навести на отрезок (прямую) (2), пересечение с которым(ой) под заданным углом нужно найти, нажать левую кнопку мыши; • на экран будет выведено окно введения параметров нового участка (3). В окне нужно ввести угол, под которым будет найдено пересечение.
• нажать кнопку Да для подтверждения действия или кнопку Отмена для отмены действия. Отрезок пересечения к кривой (дуги, сплайна) не образуется. Построение отрезка вертикальной (горизонтальной) прямой Из точки до точки пересечения с линией Для того чтобы провести из точки вертикальный отрезок до пересечения с линией, необходимо: • выбрать закладку „ Линии” (если она еще не выбрана) - навести курсор на соответствующую закладку, нажать левую кнопку мыши; • нажать кнопку • перекрестие курсора навести на точку (1), из которой будет построен вертикальный отрезок, нажать левую кнопку мыши; • перекрестие курсора навести на линию (2), которая ограничивает отрезок, нажать левую кнопку мыши;
Рис.1 рис.2 на экран будет выведено окно введения параметров, в котором, по желанию, можно изменить название отрезка и второй его конечной точки (3) и ввести текст комментария; • нажать кнопку Да для подтверждения действия или кнопку Отмена для отмены действия. В результате построена вертикальная прямая (1-3) из точки (1) до линии (2) (см. рис.1). Чтобы провести из точки горизонтальную прямую до пересечения с линией, необходимо выполнить те же действия, но после выбора кнопки команды нужно нажать клавишу клавиатуры CTRL (для перехода во второй режим работы этой функции). В результате построим горизонтальный отрезок (1-3) с точки (1) до линии (2) (см. рис.2).
|
||||
|
Последнее изменение этой страницы: 2019-04-30; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.122 (0.005 с.) |

 , и нажать левую кнопку мыши;
, и нажать левую кнопку мыши; кнопочного меню, курсор примет вид
кнопочного меню, курсор примет вид  ; или выполнить пункт меню Линии/Отрезок из точки под углом к линии;
; или выполнить пункт меню Линии/Отрезок из точки под углом к линии;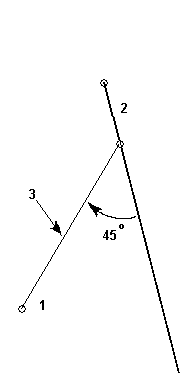

 кнопочного меню, курсор принимает вид
кнопочного меню, курсор принимает вид  , или выполнить пункт меню Линии/Вертикаль (горизонталь) к линии;
, или выполнить пункт меню Линии/Вертикаль (горизонталь) к линии;



