
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез схемы программируемого сдвигателяСодержание книги
Поиск на нашем сайте
Сдвигателем называется комбинационное цифровое устройство, реализующее операцию сдвига исходного двоичного числа в соответствии с заданием направления и шага сдвига. При разрядности сдвигаемого числа n=4, сдвигатель должен иметь n=4 информационных и c=3 управляющих входов [c=(1+log2n)], а также m=10 информационных выходов (m=3*n-2). УГО сдвигателя представляет собой прямоугольник с аббревиатурой SH внутри. Приведем назначение выводов сдвигателя согласно рисунка 2.7: D – вход управления направлением сдвига; S1, S0 – входы управления шагом сдвига;
X4…X1 – входы подачи разрядов числа X; Y6…Y0; Y-1…Y-3 – выходы разрядов сдвигаемого числа.
Рисунок 2.7 – УГО сдвигателя
Рассмотрим работу сдвигателя, осуществляющего логические сдвиги в любую сторону с сохранением выдвигаемых цифр. Таблица истинности сдвигателя представлена таблицей 2.3. Таблица 2.3 дает возможность перейти к логическому описанию сдвигателя.
Таблица 2.3 – Табличное описание работы сдвигателя
Набор функций (2.19) – (2.28) позволяет построить структурную схему сдвигателя.
х4 y6 x3 y5 x2 Сдвигающая y4 x1 матрица y3 Z7 конъюнкторов y2 Z6 y1 D Управляющий Z5 y0 DC Z0 y-1 S1 Z1 y-2 Z2 y-3 S0 Z3
Рисунок 2.8 – Структурная схема комбинационного программируемого сдвигателя
Для лучшего чтения схемы в ней выделяют: - схему управляющего дешифратора DC; - схему сдвигающей матрицы коньюнкторов. На выходе сдвигателя (Рисунок 2.8) разряды двоичного слова после сдвига формируются по правилу: Y=Z*X. поясним процесс формирования значения Z на примере синтеза дешифратора.
Дешифратор – это устройство, предназначенное для обратного преобразования исходного двоичного кода п в активный сигнал на одном из выходов. Количество входов и выходов дешифратора определяется по формуле:
Y=2x, (2.29)
где, Y - число выходов дешифратора; X - число входов дешифратора. В данном случае X=3 (D,S1,S0) входов, Y=8 (Z0…Z7) выходов. УГО дешифратора приведено на рисунке 2.9.
Рисунок 2.9 – УГО дешифратора
На Рисунке 2.9 слева показаны входы дешифратора. Цифрами 1, 2, 4 – обозначены весовые коэффициенты двоичного кода. Справа показаны выходы. Цифрами 0 … 7 – обозначены выходы Z.
Таблица дешифратора имеет вид:
Таблица 2.5 – Таблица истинности дешифратора
Согласно Таблице 2.5 записываются логические выражения для выходов дешифратора в форме ДСНФ:
Выполним перевод полученных выражений (2.30)-(2.37) в базис И-НЕ:
Логическая схема дешифратора в базисе И-НЕ (ИЛИ-НЕ) приведена на рисунке 2.10.
Рисунок 2.10 – Логическая схема дешифратора в базисе И-НЕ
Выберем для схемы рисунка 2.10 следующие микросхемы серии К564: DD9 – DD13 K564ЛА9; DD14 К564ЛА8.
Разработаем логическую схему комбинационного программируемого сдвигателя двоичных чисел в базисе И-НЕ.
Для этого подставим набор функций (2.30) – (2.45) в систему логических выражений (2.19) – (2.28) и получим:
Анализируя систему выражений (2.46) – (2.55) видно, что величина Z4 не используется, т.к. при сигналах управления нулевого шага S1=S0=0 понятие “направление сдвига” теряет смысл. Выполним перевод выражений (2.46) – (2.55) в базис И-НЕ
=
Логическая схема комбинационного программируемого сдвигателя в базисе И-НЕ приведена на рисунке 2.11. Для схемы рисунка 2.11 выберем следующие микросхемы:
DD15 – DD21 K564ЛА7; DD22, DD25 К564ЛА9; DD23, DD24 К564ЛА8; DD26, DD27 К564ИР6.
Рисунок 2.11 – Логическая схема сдвигателя в базисе И-НЕ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.16.40 (0.008 с.) |

 ; (2.19)
; (2.19)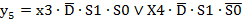 ; (2.20)
; (2.20)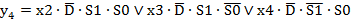 ; (2.21)
; (2.21)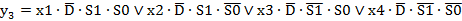 ; (2.22)
; (2.22)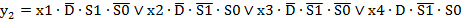 ; (2.23)
; (2.23)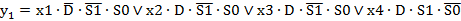 ; (2.24)
; (2.24) ; (2.25)
; (2.25) ; (2.26)
; (2.26)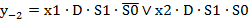 ; (2.27)
; (2.27) . (2.28)
. (2.28) (2.30)
(2.30) (2.31)
(2.31) (2.32)
(2.32) (2.33)
(2.33) (2.34)
(2.34) (2.35)
(2.35) (2.36)
(2.36) (2.37)
(2.37)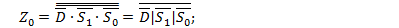 (2.38)
(2.38) (2.39)
(2.39)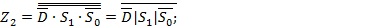 (2.40)
(2.40) (2.41)
(2.41) (2.42)
(2.42) (2.43)
(2.43) (2.44)
(2.44) (2.45)
(2.45)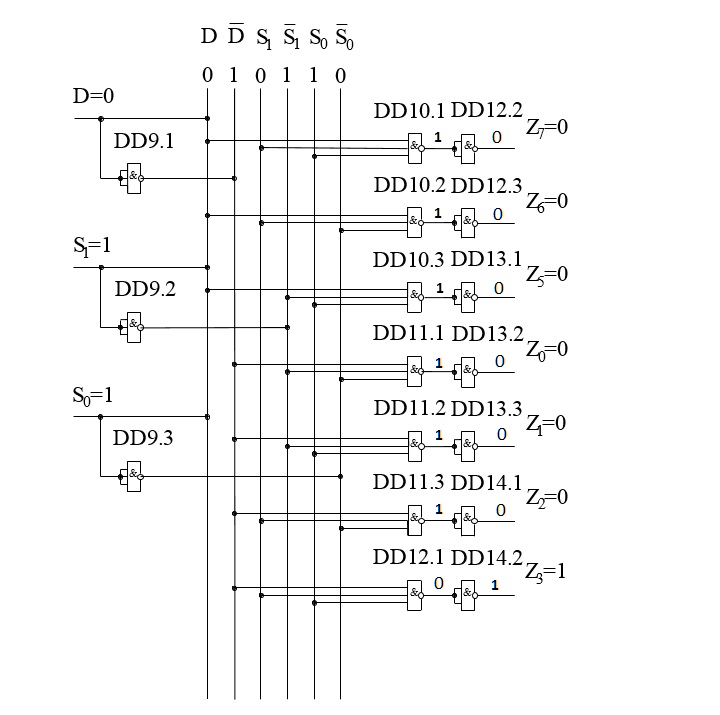
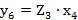 ; (2.46)
; (2.46)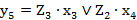 ; (2.47)
; (2.47)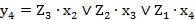 ; (2.48)
; (2.48) ; (2.49)
; (2.49) ; (2.50)
; (2.50)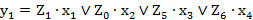 ; (2.51)
; (2.51)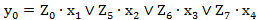 ; (2.52)
; (2.52)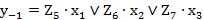 ; (2.53)
; (2.53)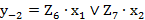 ; (2.54)
; (2.54)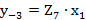 . (2.55)
. (2.55) ; (2.56)
; (2.56) ; (2.57)
; (2.57)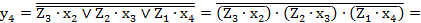
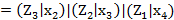 ; (2.58)
; (2.58)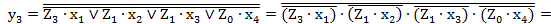
 ; (2.59)
; (2.59)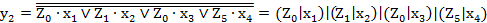 ; (2.60)
; (2.60) ; (2.61)
; (2.61)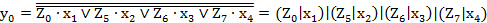 ; (2.62)
; (2.62) ; (2.63)
; (2.63)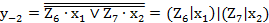 ; (2.64)
; (2.64)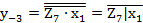 . (2.65)
. (2.65)


