Построение графиков степенных функций

 

Функция постоянная y = с = const	c 1 > 0, c 2 < 0	y
Функция линейная y = b · х + с	c 1 = 0, b 1 < 1, b 2 > 1, b 3 = –1, c 2 < 0	y = b 2 х y = b 3 х y = b 3 х +с 2   y = b 1 х
Функция квадратичная y = а · х ^2+ b · х + с	а 1 > 0, b 1 = 0, с 1 > 0, а 2 < 0, c 2 > 0

Дифференцирование и интегрирование

Математических функций

 

Функция	Производная	Интеграл
название	уравнение
Степенная	y = А · х^n	= А · n · х^n ^–^1	= = = , c – постоянная
Постоянная	y = с 1		∫ с 1 x ^0 dx = с 1 x + с, c – постоянная
Экспоненциаль- ная	y = e^х	e^х	∫ e^хdx = e^х + c c – постоянная
Логарифми- ческая	y = ln х	, х > 0	∫ ln х dx = x ln x – x+ c, c – постоянная
Тригонометри- ческие	y =sin x, y =cos x	cos x, –sin x	∫ sin x dx = –cos x+ c, ∫ cos x dx = sin x+ c, c – постоянная
Сложная	y = f 1(х), х = f 2 (t); y = sin x, х = ω · t, y = sin (ω · t)	, , ,	Не рассматривается в данном курсе физики

РАЗДЕЛ 2. ПРЕДМЕТ ФИЗИКИ

Явления, изучаемые физикой

 

Явления природы	Раздел физики
Механические (движение тел)	Механика, механические колебания
Тепловые (движение молекул)	Молекулярная физика и термодинамика
Электрические (взаимодействие и движение зарядов)	Электростатика, постоянный и переменный электрический ток
Магнитные (взаимодействие токов)	Электромагнетизм, электромагнитные колебания
Ядерные (взаимодействие и движение заряженных микрочастиц)	Атомная и ядерная физика

 

 

2.2. Место и роль физики в системе других наук (дисциплин)

 

 

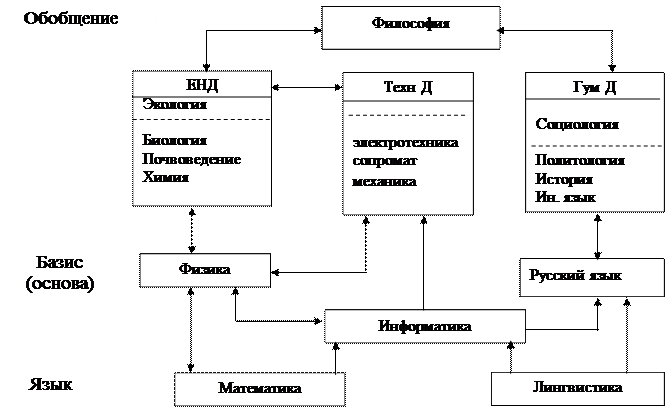
Виды материи и движения

 

 

Единицы измерений основных и дополнительных

Физических величин в системе «СИ»

№ п/п	Название	Обозначение	Единица
	Линейное перемещение (длина)	ℓ	м	метр
	Масса	m	кг	килограмм
	Время	t	с	секунда
	Сила тока	J	А	ампер
	Сила света	I	Kд	кандела
	Температура термодинамическая	Т	К	кельвин
	Количество вещества	ν	моль	моль
1 доп.	Угол	φ	pад	радиан
2 доп.	Стереоугол	ψ	сp	стерадиан

 

 

Множители и приставки кратных и дольных единиц

 

Кратные единицы	Дольные единицы
Приставка	Обозначение	Множитель	Приставка	Обозначение	Множитель
экса	Э	10^18	деци	д	10^–1
пета	П	10^15	санти	с	10^–2
тера	Т	10^12	милли	м (m)	10^–3
гига	Г	10^9	микро	мк (μ)	10^–6
мега	М	10^6	нано	н	10^–9
кило	к	10^3	пико	п	10^–12
гекто	г	10^2	фемто	ф	10^–15
дека	да	10^1	атто	а	10^–18

 

 

РАЗДЕЛ 3. МЕХАНИКА

Виды механики

 

№ п/п	Название	Основоположник	Границы применимости	Массы	Скорости	Сравнение скоростей движения со скоростью света в вакууме
	Классическая	Ньютон	макромир	средние	малые	υ << с
	Космическая	Кеплер	космос	сверхбольшие	средние	υ < с
	Релятивистская	Эйнштейн	микромир	сверхмалые	сверхбольшие	υ ≈ с
	Квантовая	Планк	микромир	сверхмалые	разные	0 ≤ υ ≤ с

Система отчёта

 

 

СО = ТО + СК + Ч

 

№ п/п	Система отчёта	Вид движения системы отчёта	Ускорение системы отчёта	Движение тел в системе отчёта	Выполнение законов Ньютона	Сила инерции
	ИСО	РМ, ПЛ	aτ = 0, an = 0	любое	выполня- ются
	НеИОС	ПЛ   РУ РЗ	an = 0, aτ = const, aτ > 0, aτ < 0	покоится	не выполняются
	НеИСО	РМ по окружности	aτ = 0, an = const,	1) покоится   2) РМ, ПЛ	не выполняются   не выполняются

Физические модели

	Материальная точка	Пренебрегаем формами и размерами тела по сравнению с другими расстояниями в данной задаче
	Абсолютно твёрдое тело	Пренебрегаем деформацией

 

3.4. Способы задания движения. Уравнение движения

Способ	Рисунок	Параметры и их связи	Уравнение движения
Векторный		– радиус-вектор
Координатный		ПЛ координаты	Δ x = f 1 (t) Δ y = f 2 (t) Δ z = f 3 (t)
Естественный		s – КЛ координата Δ s = s 2 – s 1	Δ s = f (t)

Общий случай криволинейного движения

 

Прямая задача кинематики для поступательного и вращательного движения.

Аналогия формул

№ п/п	Величина	Линейные величины	Угловые величины	Связь скалярных линейных и угловых величин
Векторные	Скалярные	Скалярные
	Путь (изменение положения тела)
	перемещение по хорде	Δ S = S – S 0 (м) линейный путь по траектории	Δ φ = φ – φ 0 (pад) угловой путь	Δ S = Δ φ ^. R
	Скорость (изменение положения тела за единичный промежуток времени)
а)	средняя за большой промежуток времени	по хорде			= ^. R
б)	мгновенная за бесконечно малый промежуток времени				= ω ^. R
	Ускорение – изменение скорости тела за единичный промежуток времени
а)	среднее				= ^. R
б)	мгновенное	внутрь кривизны (полное)
в)	тангенциальное (характеризует изменение υ по величине)		направлено по касательной к траектории		ατ = ε R
г)	Нормальное (характеризует изменение υ по направлению)		Направлено к центру кривизны		αn = ω ^2 R
д)	полное

Обратная задача кинематики для поступательного и вращательного движения.

Аналогия формул

 

№ п/п	Поступательное движение. Линейные величины	Вращательное движение. Угловые величины
Параметр	Формула	Вид движения	Параметр	Формула	Вид движения	Связь с дополнительными параметрами вращательного движения
	Линейная скорость	υ 0 = υ 0 = const	РУ (aτ > 0) РЗ (aτ < 0) РМ (aτ = 0)	Угловая скорость	ω = ω 0 + εt ω = ω 0 – εt ω = ω 0 = const	РУ (ε > 0) РЗ (ε < 0) РМ (ε = 0)
	Линейный путь (уравнение движения)		РУ (aτ > 0)   РЗ (aτ < 0)   РМ (aτ = 0)	Угловой путь (уравнение движения)		РУ (ε > 0)   РЗ (ε < 0)   РМ (ε = 0)