
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельні методи обчислення визначених інтегралів.????Содержание книги
Поиск на нашем сайте
При використанні методу прямокутпиків приблизне значення інтеграла визначається за формулою
де yі - значення f(х) на початку кожного 1 -го інтервалу; n- кількість відрізків, на які розділений діапазон інтегрування; a - нижня межа інтегрування; b - верхня межа інтегрування. У методі трапеції інтервал інтегрування [а, b] поділяється на n рівних відрізків довжиною h=
У методі Сімпсона інтервал інтегрування [а, b] поділяеться на парне число рівних відрізків довжиною
Етапи алгоритму: • знаходження значень функції з парними індексами
• знаходження значень функції з непарними індексами
• обчислення інтегралу
Через х в алгоритмі позначений аргумент, що відповідає парним номерам індексів, а через z -непарним номерам.
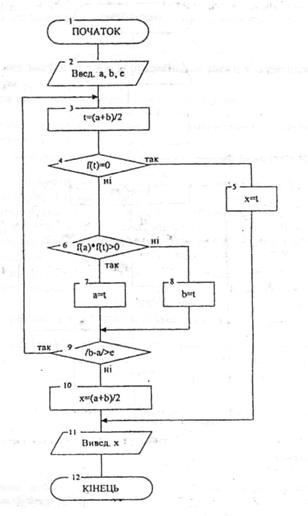
23. Методи приблизного розв'язання нелінійних рівнянь. Припустимо маємо рівняння у=f(x),де функція неперервна на відрізку [a;b] F(a)*f(b)>0 Для знаходження кореня рівняння ділимо відрізок навпіл х0=а+b/2, якщо при цьому функція у цій точці дорівнює 0, то х0 є коренем рівняння, якщо f(х0)≠0, то обираємо той відрізок [a;x0],[ x0;b]на кінцях якого f(x) має протилежні знаки. Обрані відрізки знову ділемо павпіл до того моменту поки довжина відрізку, на кінцях якого f(x) має протилежні знаки, не буде менше заданої точності Ԑ. Алгоритм метода половинного ділення:
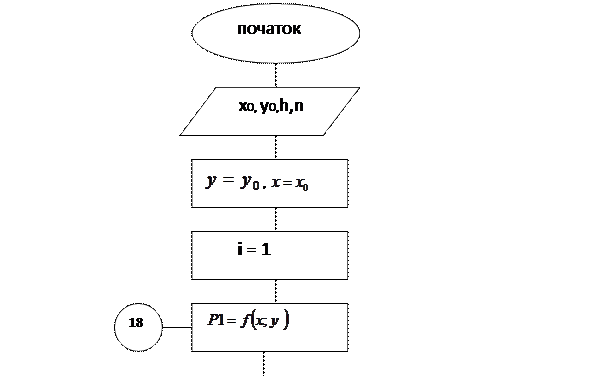
24. Чисельні методи рішення диференціальних рівнянь. Для вирішення диференціальних рівнянь I порядку використовуються методи Ейлера та Рунге Кутта.Особливість методів- для рішення диференціальних рівнянь треба знайти рішення функції, яка обчислюється циклічно. У методі Ейлера кожне наступне значення функції y= f (x,y) обчислюється по формулі y=(і+1)+ yі+ f (xі;yі)h і=0,1,2….n Аналогічно в методі Рунге Кутта:
і=0,1,2….n
Блок-схема алгоритму Рунгі Кутта
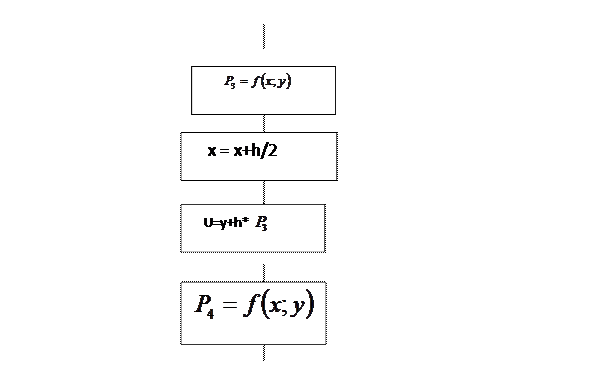
так
25.Чисельні методи інтерполяції функції. Постановка задачі. Задача інтерполяції в загальному вигляді формулюється наступним чином. Нехай на відрізку [А,В] задані значення невідомої функції y=f(x) в n різних точках х1,х2,…,хn. Потрібно знайти багаточлен Р(х) ступеню n приблизно виражаючий функцію y=f(x). Геометрична інтерпретація метода.
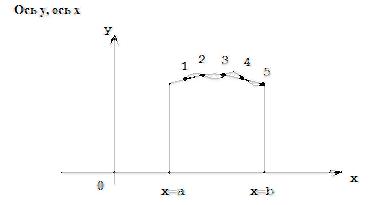
Відповідні від х називаються вузлами інтерполяції. F(x1)=y1 F(x2)=y2 F(xn)=yn Поліном Ln(x) не вище ступеню n приймає в інтерполяції ті ж самі значення, що і функція. Відповідно Ln(x1)=y1 Ln(x2)=y2 Ln(xn)=yn Розглянемо задачу з використанням інтерполяційної формули Лагранжа. Fj
Sj Де xi і змінюється від 1 до N – точки інтерполяції, yi j змінюється від 1 до N – значення функції в точках інтерполяції. N – кількість точок інтерполяції z – значення аргументу при якому необхідно вичислити значення функції. Алгоритмізація задачі. Введемо переобозначення і представимо інтерполяційну формулу наступним чином
Визначемо додатково введені змінні j=1…N i=1…N i≠j Fj+1=Fj•(z – xi) F0=1 Sj+1=Sj•(xj – xi) S0=1 Отримана інтерполяційна формула дозволяє вирахувати приблизні значення функції F(x) в точках відмінних від вузлів інтерполяції. Блок – схема алгоритму


Ні

НІ

Методи обробки експериментальних даних. Припустимо, що в результаті вимірювань отримана таблиця деякої залежності Х: Х Х 1 Х2 Х3 Х4…Хn F(x) y1 y2 y3 y4…yn У даному випадку можна використати метод інтерполяції,побудувати інтерполяційний поліном (Лагранжа),значення якого в точках від Х1 до Хnбудуть співпадати з відповідними значеннями F(x) y1… yn. Для того,щоб з самого початку обов’язково враховувався характер початкової функції необхідно знайти функцію заданого виду y=f(x),котра в точках приймає значення як можна ближчі до табличних значень y1… yn y
X1 x2 x3 x4 xn F(x,a,b)=1/(ах+b) A=P*G*B/N*F*G^2 G=ΣXi S=ΣYi P=ΣXiYi
F=ΣXi^2 M=ΣYi^2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.218 (0.009 с.) |

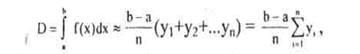
 з наступним визначенням суми площин елементарних трапецій, що апроксимують підінтегральну функціюПриблизне значения інтегралу визначається за формулою
з наступним визначенням суми площин елементарних трапецій, що апроксимують підінтегральну функціюПриблизне значения інтегралу визначається за формулою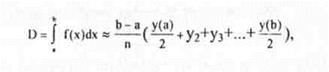
 h=
h= 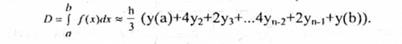
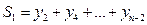
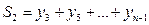
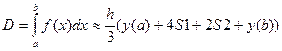
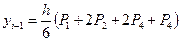

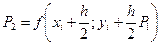
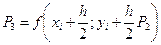


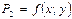





 ні
ні
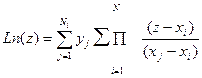 ; i≠j
; i≠j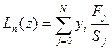


 2
2



 6
6

 да
да

















 X
X



