
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение желаемой лачх. Определение устойчивости, расчет и построение переходной характеристики скорректированной системы.Содержание книги
Поиск на нашем сайте
Существует несколько инженерных расчетных методов синтеза систем автоматики, если понимать эту задачу ограниченно. Наиболее удобен и часто употребляется при инженерных расчетах метод логарифмических частотных характеристик проф. В.В. Солодовникова. Логарифмические характеристики строятся для разомкнутых систем.
где Lку(ω корректирующего устройства; Lж(ω) – ЛАЧХ желаемой системы; Lисх(ω) – ЛАЧХ исходной системы. Построим ЛАЧХ исходной системы.
Этой передаточной функции соответствует амплитудно-фазовая и амплитудно-частотная характеристики:
Выражение для точной ЛАЧХ, исходя из этого выражения таково
Сопрягающие частоты исходной ЛАЧХ находятся следующим образом:
Так как передаточная функция исходной разомкнутой системы относится к III типу, то для первого участка асимптотической ЛАЧХ, т. е. для ω<ωс1=1,54 с-1, уравнения асимптоты ЛАЧХ будет: L1 исх (ω)=32-20lgω Это уравнение прямой линии с наклоном -20 дб/дек, проходящий при ω=1с через точку L1исх(1)=32дб. Дальнейший ход асимптотической ЛАЧХ при увеличении частоты характеризуется тем, что на сопрягающих частотах ωс1, ωс2 и ωс3 происходит изменения наклона характеристики каждый раз на -20дб/дек. (рис.7).
Рис. 7. ЛАЧХ исходной, желаемой САР и КУ
Теперь построим желаемую ЛАЧХ. т. е. ЛАЧХ устойчивой системы, отвечающей заданным требованием к качеству регулирования. Определим сначала частоту среза (при σ=35%, b=4,4):
Среднечастотный участок Lж(ω) проходит через частоту среза с наклоном -20 дб/дек. Длину среднечастотной асимптоты ограничим слева произвольной частотой ω∆=0,1, с права – частотой ωс1,т.е. ближайшей точкой излома Lисх(ω). Низкочастотный участок Lисх(ω) и Lж(ω) совпадают и осуществляется отрезком прямой с наклоном -20 дб/дек. Высокочастотный участок желаемой ЛАЧХ содержит высокие гармоники и слабо влияет на переходный процесс в системе, поэтому ее (ЛАЧХ этого участка) вид может быть достаточно произвольным. Для большей простоты корректирующего устройства высокочастотный участок ЛАЧХ желаемой САР Lж(ω) проводим параллельно с таким же участком исходной ЛАЧХ Lисх(ω). Среднечастотный участок желаемой ЛАЧХ сопряжем с низкочастотным и высокочастотным участками желаемой ЛАЧХ асимптотами с наклоном – 40дб/деккаждый. Построенная таким образом асимптотическая Lж(ω) представлена на рис.7. Найдем точку пересечения Lж(ω) и Lисх(ω): Lсрж(0,1)=20lg0,95-20lg0,1=-20,45; Lсопр(ω)=20lgKсопр-40lg0,1=-20,45; 20lgKсопр=40lg0,1-20,45; 20lgKсопр=-60,45; lgKсопр=-3,02; Kсопр=0,55; 20lg0,55-40lgω*=32-20lg ω*; -5,19-40lgω*=32-20lg ω*; -20lgω*=37,19; lgω*=-1,86; ω*=0,003 (Т3=1/ω*=1/0,003=333,33с); Передаточная функция разомкнутой желаемой системы может быть, исходя из Lж(ω) записана следующим образом:
Проверим, устойчива ли желаемая система. Поскольку уже построена Lж(ω),устойчивость замкнутой желаемой системы удобнее оценить с помощью логарифмического критерия. Базируясь на передаточную функцию разомкнутой желаемой САР, найдем фазовую частотную характеристику этой системы: φж(ωсрж)=-π/2+arctg10 ωсрж- arctg4,17 ωсрж –arctg0,65ωсрж –arctg0,04ωсрж – -arctg0,3ωсрж=-90+84,3-75,12-31,7-0,04-15,91=-128,47; При этом запас устойчивости по фазе будет: γ=180-128,47=51,53>0, значит, желаемая САР в замкнутом состоянии устойчива. Для проверки соответствия показателей качества регулирования желаемой системы заданным требованиям построим переходную характеристику замкнутой желаемой САР h3ж(t).
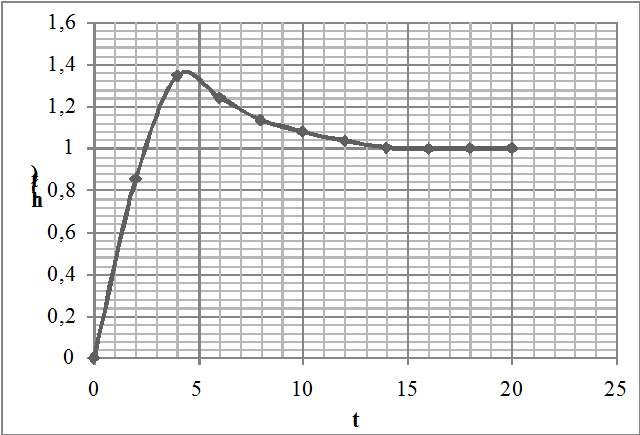
Переходную характеристику замкнутой желаемой системы находим через MathCAD: h3ж(t)=0,033*e-27,22t-0,001*e-0,1t+0,34*e-10,97t-0,69*e2,64t*cos(6,2t)- -0,16*e2,64t*sin(6,2t) +1 Для построения графика переходной характеристики h(t) (рис.8), воспользуемся таблицей 2. Таблица 2
Рис. 8. График переходной функции h(t).
Из таблицы 2 видно, что tp, т.е. время, после которого переходный процесс h3ж(t) не выйдет из коридора [1, стр.161]: (1±∆)Zуст=(1±0,024)*1=0,976÷1,024, составляет приблизительно tp=14, что удовлетворяет заданию (tпп≤14,5). Из таблицы можно посмотреть, что максимальное значение h(t)=1,346 получается при t=4,а значит перерегулирование желаемой системы будет:
Таким образом, желаемая система устойчива и удовлетворяет поставленным требованиям к качеству регулирования.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 3653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.66 (0.009 с.) |

 , [1, стр.166] (21)
, [1, стр.166] (21)

 . [1, стр.64] (22)
. [1, стр.64] (22)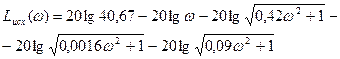 . [1, стр.74] (23)
. [1, стр.74] (23)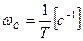 [1, стр.75] (24)
[1, стр.75] (24) ,
, ,
,

 . [1, стр.162] (25)
. [1, стр.162] (25) Желаемая замкнутая САР будет характеризоваться передаточной функцией:
Желаемая замкнутая САР будет характеризоваться передаточной функцией: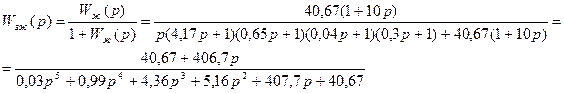
 . [1, стр.167] (26)
. [1, стр.167] (26)
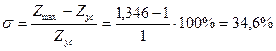 [1, стр.161]
[1, стр.161]


