
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание принципиальной схемы САУСодержание книги Поиск на нашем сайте
Принцип работы САР напряжения генератора
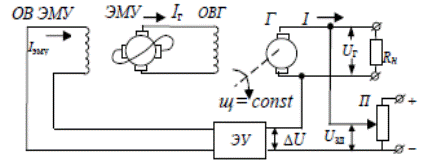
Рис. 2. Принципиальная электрическая схема статической САР напряжения генератора.
Здесь обозначено Г – генератор, якорь которого вращается от постороннего двигателя с постоянной угловой скоростью ω=const; ОВГ – обмотка возбуждения генератора; ЭМУ – электромашинный усилитель, предназначенный для усиления сигнала по току; ОВ ЭМУ – обмотка возбуждения электромашинного усилителя; ЭУ – электронный усилитель для усилений сигнала по напряжению; Rн – сопротивление нагрузки генератора; Iэму, Iг, I - токи, соответственно, в обмотках возбуждения ЭМУ, Г и в нагрузке; П – потенциометр задания. Здесь объектом управления ОУ является генератор со своей ОВГ, все остальные элементы схемы составляют регулирующее устройство РУ. Цель САР – обеспечить поддержание постоянства напряжения генератора при изменении его нагрузки. Величина напряжения Uг, которую генератор должен поддерживать с некоторой точностью на своих зажимах, несмотря на колебания Rн, задается с помощью напряжения Uзд, снимаемого с потенциометра П. Непосредственно из рис. 2 можно получить зависимости, которые понадобятся нам в дальнейшем: UГ = Ег– I Rя и (1) ∆U = Uзд – Uг, (2) где Ег– ЭДС генератора, Rя – сопротивление якорной цепи. Из принципиальной схемы САР напряжения генератора получим функциональную схему. Начинать построение функциональной схемы рекомендуется с сумматора, который в принципиальной схеме представлен частью электрической схемы, предназначенной для сравнения сигналов Uзд и Uг. Полученный в соответствии с формулой (2) сигнал рассогласования ∆U поступает далее по цепочке – ЭУ, ЭМУ, Г. Выходной сигнал генератора по цепи отрицательной обратной связи поступает на сумматор. Отметим также, что на генератор воздействует возмущение Rн.
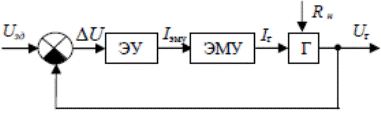
Рис. 3. Функциональная схема статической САР напряжения генератора.
В установившемся режиме напряжение генератора Uг, а, следовательно, и Iг, и Iэму постоянны. Пусть в некоторый момент времени нагрузка на генератор скачкообразно изменится (допустим, ток нагрузки I скачком возрастёт). Из (1) видно, что в этом случае Uг в первый момент скачком уменьшится, а напряжение рассогласования ∆U согласно (2) скачком возрастёт. Этот сигнал ∆U после усиления будет в процессе регулирования восстанавливать упавшее в первый момент напряжение Uг. До какого значения будет подниматься этот сигнал Uг? Будет ли он равен после окончания переходного процесса напряжению Uзд? В статической САР – никогда. Действительно, в случае равенства Uг и Uзд согласно (2) ∆U будет равно нулю, а это означает, что и IЭМУ, и Iг и, самое главное, Uг должны быть равны нулю, что противоречит назначению САР – поддерживать с некоторой точностью постоянным заданное напряжение на зажимах генератора. Таким образом, наличие в установившемся режиме статической ошибки ∆U≠0 является необходимым для функционирования системы. Именно эта ошибка ∆U после ее усиления электронным и электромашинным усилителями определяет величину Uг. Нетрудно понять, что величина этой статической ошибки обратно пропорциональна коэффициенту усиления прямой цепи (см. рис. 3), ибо, чем больше этот коэффициент усиления, тем меньше должна быть ошибка ∆U, чтобы получить требуемое Uг. Перейдем теперь к математической стороне дела. Рассмотрим сначала отдельно взятый генератор без регулирующего устройства. Следовательно, изменение напряжения на генераторе в установившемся режиме при изменения нагрузки от I = 0 до I = Iн без регулирующего устройства ∆Uг без ру (т.е. статическая ошибка, соответствующая указанному изменению нагрузки) будет ∆U г без ру = Uгхх – Uгн = Е г – Ег + I нR н = I нR я. (3)
При номинальной нагрузке появляется статическая ошибка
Из сравнения (3) и (5) ясно, что в САР напряжения генератора по сравнению с одиночным генератором (без регулирующего устройства) статическая ошибка уменьшается в (1 + k) раз. Рассмотрим статические характеристики САР генератора при наличии и отсутствии регулирующего устройства (рис. 4).
Рис. 4. Статические характеристики САР при наличии (2) и отсутствии (1) регулирующего устройства
Для удобства примем при холостом ходе Видно, что для различных значений нагрузки появляется различная по величине статическая ошибка (она растет с ростом тока нагрузки I), причем для САР с регулирующим устройством статическая ошибка значительно меньше, чем без регулирующего устройства. Из (5) ясно, что для уменьшения статической ошибки надо увеличивать коэффициент усиления системы k, имея, правда, в виду, что с ростом k уменьшается устойчивость системы.[1]
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.81.143 (0.006 с.) |

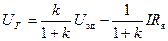 (4)
(4)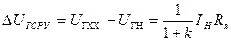 . (5)
. (5)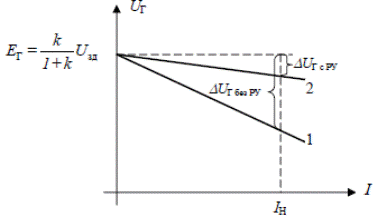
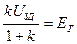 , тогда статические характеристики САР при наличии и отсутствии регулирующего устройства начнутся при I = Iхх = 0 из одной точки.
, тогда статические характеристики САР при наличии и отсутствии регулирующего устройства начнутся при I = Iхх = 0 из одной точки.


