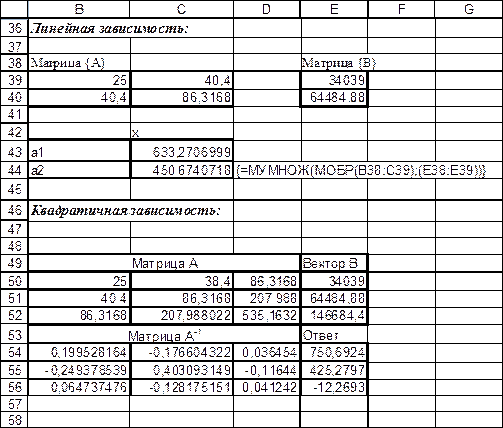Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задачи в среде Turbo PascalСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вычислим приближённые функции методом наименьших квадратов в среде программирования Turbo Pascal. Сформируем систему линейных алгебраических уравнений, и решим методом Гаусса. Алгоритм программы Turbo Pascal для вычисления коэффициентов линейной функции, приближённой к экспериментальным данным:
Блок-схема 1
Алгоритм программы Turbo Pascal для вычисления коэффициентов квадратичной функции, приближённой к экспериментальным данным:
Блок-схема 2 Для составления СЛАУ необходимо вычислить суммы, являющиеся элементами матрицы коэффициентов. Напишем программу, вычисляющую суммы. Описание программы Рассмотрим наиболее важные функции и процедуры, используемые для вычисления сумм (элементов матрицы коэффициентов) квадратичной функции: Процедура ASSIGN используется для связывания файловой переменной с именем файла. В общем виде записывается следующим образом: ASSIGN (<файловая переменная>, <имя файла или логическое устройство>); Конкретно в курсовой работе процедура ASSIGN представлена в следующем виде: assign(fw,'gaus.txt'); assign(fm,kursovik.txt'); На языке Turbo Pascal имеются три различных оператора, с помощью которых можно запрограммировать повторяющиеся фрагменты программ. В данной программе используется счётный оператор цикла FOR., который используется для вычисления сумм всех чисел от 1 до n. В общем виде записывается следующим образом: FOR <параметр_цикла>:= <начальное_значение> ТО <конечное_значение> DO <оператор> FOR, TO, DO - зарезервированные слова (для, до, выполнить). Конкретно в курсовой работе цикл FOR используется для проведения циклического процесса вычисления сумм, являющихся элементами исходной матрицы коэффициентов: FOR i:=1 TO 25 DO Begin a1:=a1+X1[i]; {для x(i)} b1:=b1+Y1[i]; {для y(i)} c1:=c1+sqr(X1[i]); {для x(i)2} d1:=d1+X1[i]*Y1[i]; {для x(i)y(i)} e1:=e1+X1[i]*X1[i]*X1[i]; {для x(i)3} f1:=f1+X1[i]*X1[i]*X1[i]*X1[i]; {для x(i)4} g1:=g1+X1[i]*X1[i]*Y1[i]; {для x(i)2y(i)} end; Решение СЛАУ методом Гаусса Метод Гаусса – один из точных методов решения систем. Он состоит из прямого и обратного ходов. При прямом ходе матрица, составленная из коэффициентов уравнений системы, приводится к треугольному виду так, чтобы ниже ее главной диагонали оказались нули. Рассмотрим метод подробнее для системы:
Предположим, что
и вычтем из каждого i -го уравнения первое, помноженное на Обозначая легко убедится, что для всех уравнений, начиная со второго,
Преобразованная система уравнений запишется в следующем виде:
Аналогичным образом исключим х2 из последних (n-2) уравнений, получив новые коэффициенты. Эту операцию будем проводить пока система не примет вид:
Обратный ход. Он состоит в нахождении значений системы по формулам: из последнего уравнения вычисляем
Вывод В курсовой работе рассмотрено два варианта теоретической зависимости момента нагрузки M [кг·м] исполнительного органа угольного комбайна от толщины среза h [см] в MathCad и на языке программирования Turbo Pascal 7.0. Вычисления независимых расчётов сходятся, следовательно, – расчёты верны. В результате получились следующие формулы:
Давая качественную оценку коэффициентам детерминированности, опираясь на шкалу Чеддока, можно утверждать, что при линейной и квадратичной аппроксимациях наблюдается «весьма высокая» теснота связи между независимой переменной и предикатом (0,9–0,99), а это еще раз свидетельствует о правильности выбора функций для аппроксимации. При сравнении этих коэффициентов можно сказать, что уравнение линейной зависимости ( Библиографический список
Приложение 1
Приложение 2
Приложение 3 PROGRAM lineynaya; {подключение модуля, необходимого для процедур очистки экрана и задержки} USES CRT; {Задание массива} TYPE MAT=ARRAY [1..10,1..11] OF REAL; VEK=ARRAY [1..25] OF REAL; {Описание переменных} VAR i,j,n:INTEGER; A:MAT; X,B,X1,Y1:VEK; fr,fm:text; a1,b1,c1,d1:real; {Процедура Гаусса} PROCEDURE GAU(VAR A:MAT; VAR B,X:VEK; m:INTEGER); VAR k,i,j,t,L:INTEGER; D:REAL; fw:TEXT; BEGIN {Задание всех переменных} L:=m+1; FOR i:=1 TO m DO A[i,L]:=B[i]; {имя файла данных на диске} ASSIGN(fw,'gaus.txt'); REWRITE(fw); {запись данных в файл} WRITELN(fw,' CUCTEMA YPABHEHIY: '); {начальный вывод данных} FOR i:=1 TO m DO BEGIN FOR j:=1 TO m DO WRITE(fw,A[i,j]:14:6,' X[',j,'] '); WRITELN(fw,' = ', B[i]:14:6); END; {прямой ход решения СЛАУ по методу Гаусса} {формирование треугольной матрицы коэффициентов} FOR i:=1 TO m DO BEGIN D:=A[i,i]; t:=i; {ищем max в столбце} FOR j:=i TO m DO IF abs(A[j,i]) > abs(D) THEN BEGIN D:=A[j,i]; t:=j;END; {обмен строк} IF i<>t THEN BEGIN FOR j:=i TO L DO BEGIN D:=A[i,j]; A[i,j]:=A[t,j]; A[t,j]:=D;END; END; {формирование строки} FOR j:=L DOWNTO i DO A[i,j]:=A[i,j]/A[i,i]; {зануление столбцов и пересчет А} FOR k:=i+1 TO m DO FOR j:=L DOWNTO i DO A[k,j]:=A[k,j]-A[i,j]*A[k,i]; END; {обратный ход} X[m]:=A[m,L]; FOR i:=m-1 DOWNTO 1 DO BEGIN D:=0; FOR j:=m DOWNTO i+1 DO D:=D+A[i,j]*X[j]; X[i]:=A[i,L]-D; END; WRITELN(fw,' VEKTOR X: '); FOR i:=1 TO m DO WRITE(fw, X[i]:10:6); WRITELN(fw); CLOSE(fw) END; {вычисление сумм} BEGIN clrscr; {имя файла данных на диске} assign(fm,'kursovik.txt'); reset(fm); {чтение данных c файла} FOR i:=1 TO 25 DO read(fm,X1[i]); FOR i:=1 TO 25 DO read(fm,Y1[i]); FOR i:=1 TO 25 DO {формулы вычисления для сумм} begin a1:=a1+X1[i]; {для x(i)} b1:=b1+Y1[i]; {для y(i)} c1:=c1+sqr(X1[i]); {для x(i)2} d1:=d1+X1[i]*Y1[i]; {для x(i)y(i)} end; {имя файла данных на диске} assign(fr,'dan.txt');REWRITE(fr); {запись данных в файл} {Формирование матрицы А} write(fr,25,' '); writeln(fr,a1:4:4,' '); write(fr,a1:4:4,' '); writeln(fr,c1:4:4,' '); write(fr,b1:4:4,' '); writeln(fr,d1:4:4,' '); close(fr);
WRITELN(' РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА. КОЛ-ВО УРАВН. НЕ БОЛЕЕ 10'); WRITELN; WRITE(' ВВОДИ ЧИСЛО УРАВНЕНИЙ: '); READLN(n); {имя файла данных на диске} assign(fr,'dan.txt'); reset(fr); {чтение данных с файла} FOR i:=1 TO n DO FOR j:=1 TO n DO READ(fr,A[i,j]); FOR i:=1 TO n DO READ(fr,B[i]); for i:=1 to n do begin for j:=1 to n do write(a[i,j]:14:6); writeln(B[i]:14:1); end; GAU(A,B,X,n); {вывод результатов} WRITELN('VEKTOR X:'); FOR i:=1 TO n DO WRITE(X[i]:12:6,' '); WRITELN; readln; END.
Результат работы программы CUCTEMA YPABHEHIY: 25.000000 X[1] 40.400000 X[2] = 34039.000000 40.400000 X[1] 86.316800 X[2] = 64484.880000 VEKTOR X: 633.272700 450.674072
Приложение 4 PROGRAM kvadratichnaya; {подключение модуля, необходимого для процедур очистки экрана и задержки} USES CRT; {Задание массива} TYPE MAT=ARRAY [1..10,1..11] OF REAL; VEK=ARRAY [1..25] OF REAL; {Описание переменных} VAR i,j,n:INTEGER; A:MAT; X,B,X1,Y1:VEK; fr,fm:text; a1,b1,c1,d1,e1,f1,g1:real; {Процедура Гаусса} PROCEDURE GAU(VAR A:MAT; VAR B,X:VEK; m:INTEGER); VAR k,i,j,t,L:INTEGER; D:REAL; fw:TEXT; BEGIN {Задание всех переменных} L:=m+1; FOR i:=1 TO m DO A[i,L]:=B[i]; {имя файла данных на диске} ASSIGN(fw,'gaus.txt'); REWRITE(fw); {запись данных в файл} WRITELN(fw,' CUCTEMA YPABHEHIY: '); {начальный вывод данных} FOR i:=1 TO m DO BEGIN FOR j:=1 TO m DO WRITE(fw,A[i,j]:14:6,' X[',j,'] '); WRITELN(fw,' = ', B[i]:14:6); END; {прямой ход решения СЛАУ по методу Гаусса} {формирование треугольной матрицы коэффициентов} FOR i:=1 TO m DO BEGIN D:=A[i,i]; t:=i; {ищем max в столбце} FOR j:=i TO m DO IF abs(A[j,i]) > abs(D) THEN BEGIN D:=A[j,i]; t:=j;END; {обмен строк} IF i<>t THEN BEGIN FOR j:=i TO L DO BEGIN D:=A[i,j]; A[i,j]:=A[t,j]; A[t,j]:=D;END; END; {формирование строки} FOR j:=L DOWNTO i DO A[i,j]:=A[i,j]/A[i,i]; {зануление столбцов и пересчет А} FOR k:=i+1 TO m DO FOR j:=L DOWNTO i DO A[k,j]:=A[k,j]-A[i,j]*A[k,i]; END; {обратный ход} X[m]:=A[m,L]; FOR i:=m-1 DOWNTO 1 DO BEGIN D:=0; FOR j:=m DOWNTO i+1 DO D:=D+A[i,j]*X[j]; X[i]:=A[i,L]-D; END; WRITELN(fw,' VEKTOR X: '); FOR i:=1 TO m DO WRITE(fw, X[i]:10:6); WRITELN(fw); CLOSE(fw) END; {вычисление сумм} BEGIN clrscr; {имя файла данных на диске}
assign(fm,'kursovik.txt'); reset(fm); {чтение данных c файла} FOR i:=1 TO 25 DO read(fm,X1[i]); FOR i:=1 TO 25 DO read(fm,Y1[i]); FOR i:=1 TO 25 DO {формулы вычисления для сумм} begin a1:=a1+X1[i]; {для x(i)} b1:=b1+Y1[i]; {для y(i)} c1:=c1+sqr(X1[i]); {для x(i)2} d1:=d1+X1[i]*Y1[i]; {для x(i)y(i)} e1:=e1+X1[i]*X1[i]*X1[i]; {для x(i)3} f1:=f1+X1[i]*X1[i]*X1[i]*X1[i]; {для x(i)4} g1:=g1+X1[i]*X1[i]*Y1[i]; {для x(i)2y(i)} end; {имя файла данных на диске} assign(fr,'dan.txt');REWRITE(fr); {запись данных в файл} {Формирование матрицы А} write(fr,25,' ',a1:4:4,' '); writeln(fr,c1:4:4,' '); write(fr,a1:4:4,' ',c1:4:4,' '); writeln(fr,e1:4:4,' '); write(fr,c1:4:4,' ',e1:4:4,' '); writeln(fr,f1:4:4,' '); write(fr,b1:4:4,' ',d1:4:4,' '); writeln(fr,g1:4:4,' '); close(fr); WRITELN(' РЕШЕНИЕ СЛАУ МЕТОДОМ ГАУССА. КОЛ-ВО УРАВН. НЕ БОЛЕЕ 10'); WRITELN; WRITE(' ВВОДИ ЧИСЛО УРАВНЕНИЙ: '); READLN(n); {имя файла данных на диске} assign(fr,'dan.txt'); reset(fr); {чтение данных с файла} FOR i:=1 TO n DO FOR j:=1 TO n DO READ(fr,A[i,j]); FOR i:=1 TO n DO READ(fr,B[i]); for i:=1 to n do begin for j:=1 to n do write(a[i,j]:14:6); writeln(B[i]:14:1); end; GAU(A,B,X,n); {вывод результатов} WRITELN('VEKTOR X:'); FOR i:=1 TO n DO WRITE(X[i]:12:6,' '); WRITELN; readln; END.
Результат работы программы CUCTEMA YPABHEHIY: 25.000000 X[1] 40.400000 X[2] 86.316800 X[3] = 34039.000000 40.400000 X[1] 86.318600 X[2] 207.988022 X[3] = 64484.880000 86.318600 X[1] 207.988022 X[2] 535.163222 X[3] = 146684.350400 VEKTOR X: 412.112901 848.450296 -122.122397
Приложение 5
Приложение 6
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.56.35 (0.01 с.) |


 (11)
(11) не равно нулю. Введем (n-i) множителей
не равно нулю. Введем (n-i) множителей (12)
(12) (13)
(13) . (14)
. (14) (15)
(15) (16)
(16) , далее находим
, далее находим  и из 1-го уравнения системы вычисляем:
и из 1-го уравнения системы вычисляем:
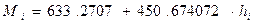 ,
, .
. ) удовлетворительно отображает экспериментальные данные. Но все же коэффициент детерминированности уравнения квадратичной зависимости ближе к единице (
) удовлетворительно отображает экспериментальные данные. Но все же коэффициент детерминированности уравнения квадратичной зависимости ближе к единице ( ) и достаточно хорошо отображает экспериментальные данные. На этом основании можно сделать вывод, что квадратичная зависимость наилучшим образом отображает взаимосвязь между M и h.
) и достаточно хорошо отображает экспериментальные данные. На этом основании можно сделать вывод, что квадратичная зависимость наилучшим образом отображает взаимосвязь между M и h.