
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование внезапных отказов
Построим интегральную функцию экспоненциального распределения:
где l — интенсивность отказов. Интенсивность отказов рассчитывается по формуле:
где Тср — среднее время наработки на отказ. Примем среднюю наработку на отказ устройства при отказе клапана Тср =30000 часов.
По расчетным данным построим интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 3¸4 раза больше Тср. На оси ординат — значение функции F (t). На основе метода «Монте-Карло» промоделируем вероятность случайных отказов. Выбрасываем с помощью генератора случайных чисел числовую последовательность R в диапазоне значений (0¸1). Отложим каждое из чисел числовой последовательности R по оси ординат, проведем прямую, параллельную оси абсцисс до пересечения с графиком функции F (t) и из точки пересечения опустим перпендикуляр на ось времени; таким образом, получаются значения времени, соответствующие каждому числу последовательности, приведенные в первой строчке табл. 2.1, которые называются реализацией времени функционирования устройства. Таких реализаций получим не менее 5 (1, 2, 3, 4, 5 строчки таблицы). Набор реализаций называется выборкой из 6´5 элементов.
F(t)
Рисунок 4. Интегральная функция экспоненциального распределения
Таблица 2 Временная выборка из пяти реализаций для шести элементов t ´103 час
Далее временные значения ti, приведенные в табл. 2, сравниваем с Тср /2, поскольку нас интересует поведение системы в первый полупериод эксплуатации. Затем получим время t 0 нерабочего состояния элемента системы Х1, выбирая лишь те случаи, когда ti < Тср /2. Расчет производится по формуле:
Полученное значение t 0 заносим в табл. 2, указав его в скобках, затем суммируем нерабочее время в единичной реализации t 0 и берем отношение к сумме общего времени tобщ работы элемента в этой реализации. На основе полученных значений определим вероятность отказа элемента системы Х1 для данной реализации по формуле:
и так для каждой реализации. Вероятность отказа элемента системы Х1 является средним арифметическим этих значений:
Моделирование постепенных отказов
Постепенные отказы подчиняются нормальному закону распределения. Интегральная функция нормального закона имеет вид:
где d — среднеквадратичное отклонение; a — математическое ожидание. Для того, чтобы не рассчитывать интеграл, воспользуемся половинной функцией Лапласа и с ее помощью рассчитаем нормальный закон распределения по формуле:
где Ф (х) — половинная функция Лапласа; х =(t - Tср)/d, где х — аргумент функции Лапласа; t — время функционирования; Тср — средняя наработка на отказ; d — среднеквадратичное отклонение. На рис. 2.6 представлен график половинной функции Лапласа.

Рассчитаем интегральную функцию F (t) нормального распределения для Х1 (износ манжет), задавшись Тср =286000 час., d=500, определим аргумент функции Лапласа и занесем данные в табл. 3.
Таблица 3. Сводная таблица расчета интегральной функции нормального распределения
На основе расчетных данных табл. 3 построим график нормального распределения. Процедура моделирования аналогична рассмотренной выше. Полученные значения сравниваем с Тср, т. к. нас интересуют характеристики системы в первый период эксплуатации. В тех случаях, если t 0< Tср, находим нерабочее время t 0 элемента системы Хi по формуле
Полный коэффициент отказа элемента системы
R X1=0,0012 R X2=0,002 R X3=0,0053 R X4=0,0049 R X5=0,0021 R X6=0,006 R X7=0,0013 для «ИЛИ» для «И» Рассчитаем коэффициент отказа системы Rкс по формуле:
где
отсюда Rкс =0,011.
Качественная и количественная оценка безопасности функционирования эргатической системы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.236.85 (0.01 с.) |
 (1)
(1) (2)
(2) t·103 ч
t·103 ч (3)
(3) (4)
(4) (5)
(5)
 (6)
(6) (7)
(7) . Затем, просуммировав время t 0 по реализации, берем отношение t 0 к суммарному времени функционирования элемента системы Х5 в этой реализации
. Затем, просуммировав время t 0 по реализации, берем отношение t 0 к суммарному времени функционирования элемента системы Х5 в этой реализации 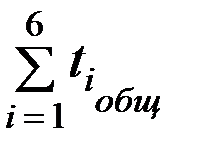 . Вероятность отказа элемента системы Х5 в данной реализации определяем по формуле:
. Вероятность отказа элемента системы Х5 в данной реализации определяем по формуле:
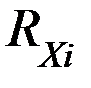 рассчитывается как
рассчитывается как


 (8)
(8)




