
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальний когерентний прийом цифрових сигналів.Содержание книги
Поиск на нашем сайте
У задачі розпізнавання сигналів, що не містять випадкових параметрів (тобто точно відомих), «причинами» є надходження на вхід сигналів Кількісно опис ситуації зручно проводити за допомогою розгляду векторів відповідних коливань. замість сигналів
Відповідно до теореми Байеса:
Як було зазначено, рішення зазвичай виноситься на користь сигналу, що має найбільшу апостеріорну ймовірність. Так як знаменник не залежить від номера I, то вирішальне правило (алгоритм рішення) визначається так:
Слід звернути увагу на те, що в цих висловах У виразі (3) апріорні ймовірності
то щільність ймовірності деякого значення вектора
Останній перехід справедливий тому, що сигнал і перешкоди - незалежні процеси. Для подальшої конкретизації алгоритму необхідно задати певний вид перешкоди. У більшості випадків мають місце нормальні (гаусові) або близькі до них перешкоди. Обчислення в цьому випадку виявляються найбільш простими. При гауссовских перешкодах кожна компонента вектора
У ряді випадків, зокрема, при рівномірному розподілі енергії перешкоди по смузі розглянутих частот, компоненти вектора
При залежних компонентах Зазначимо, що Отже,
Відкинувши множники, не залежні від номера сигналу i, вирішальне правило (3) можна представити у вигляді
Приймач, що працює за алгоритмом (8), називається байєсовський або приймачем максимальної апостеріорної ймовірності. Якщо апостеріорні ймовірності елементів
Відповідний приймач називається приймачем максимального правдоподібності. Правило (9) розкриває механізм роботи оптимального приймача. Отримавши вектор y, за допомогою обробки реалізації y (t) необхідно обчислити відстань від його кінця до кінців векторів всіх можливих сигналів Вираз (9) досягає максимуму при мінімумі показника експоненти. Отже, правило (9) можна записати в іншому вигляді:
або, враховуючи векторне уявлення
Тут перший член в дужках не залежить від номера i. Останній член - є енергія i-того сигналу. Якщо енергії всіх сигналів однакові, що зазвичай має місце, то цей член також не залежить від номера i. Таким чином, вирішальне правило можна записати так:
Справедливість такого переходу зумовлена тим, що другий член в (10) має знак мінус і вираз (10) мінімізується, якщо цей член досягає максимуму. Вираз (11) вже дозволяє визначити структуру оптимального приймача. Однак зручніше це вираз представити в іншому вигляді. Дійсно, врахуємо, що
Тоді остаточно отримаємо:
Ця структура називається оптимальним кореляційним приймачем, так як основна операція, що лежить в його основі, це операція кореляції y(t) з усіма можливими сигналами З проведеного розгляду випливає, що до складу оптимального приймача повинні входити генератори, що виробляють зразки сигналів
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.20.156 (0.01 с.) |

 , ймовірності яких рівні, очевидно, імовірності появи відповідних елементів
, ймовірності яких рівні, очевидно, імовірності появи відповідних елементів  . «Наслідками» є реалізації суми сигналу і перешкоди.
. «Наслідками» є реалізації суми сигналу і перешкоди. , а замість реалізацій y (t) - векторами
, а замість реалізацій y (t) - векторами  , координати яких визначаються виразом, який в нашому випадку запишемо так:
, координати яких визначаються виразом, який в нашому випадку запишемо так: (1)
(1) (2)
(2) (3)
(3) -- щільності ймовірностей, так як компоненти вектора y, як видно з (1), є безперервними випадковими величинами.
-- щільності ймовірностей, так як компоненти вектора y, як видно з (1), є безперервними випадковими величинами. передачи елементів
передачи елементів  ,
, дорівнює щільності ймовірності, що вектор перешкоди n набуде значення
дорівнює щільності ймовірності, що вектор перешкоди n набуде значення  . Звідси випливає, що якщо
. Звідси випливає, що якщо 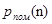 - відома нам щільність ймовірності вектора перешкоди, то
- відома нам щільність ймовірності вектора перешкоди, то (4)
(4) розподілена по нормальному закону
розподілена по нормальному закону (5)
(5) є незалежними випадковими величинами. Тоді, як відомо,
є незалежними випадковими величинами. Тоді, як відомо, (6)
(6) істотно ускладнюється і цей випадок тут розглядати не будемо.
істотно ускладнюється і цей випадок тут розглядати не будемо. , тобто є квадратом довжини (норми) вектора перешкоди.
, тобто є квадратом довжини (норми) вектора перешкоди. (7)
(7) (8)
(8) (9)
(9)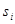 і винести рішення на користь того сигналу, для якого величина
і винести рішення на користь того сигналу, для якого величина  буде мінімальною, тому що саме в цьому випадку функція (9) досягне максимуму. Коротко можна сказати, що оптимальний приймач виносить рішення на користь сигналу «найближчого» до y (t).
буде мінімальною, тому що саме в цьому випадку функція (9) досягне максимуму. Коротко можна сказати, що оптимальний приймач виносить рішення на користь сигналу «найближчого» до y (t).
 (10)
(10) (11)
(11) (12)
(12) (13)
(13)


