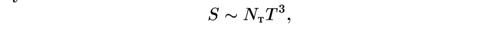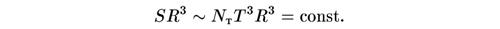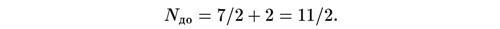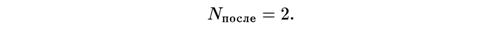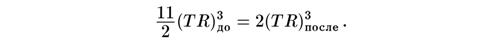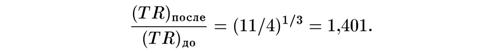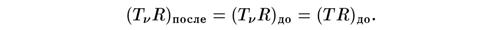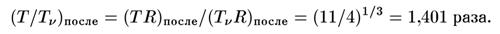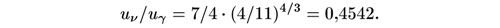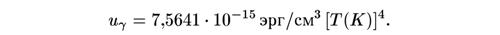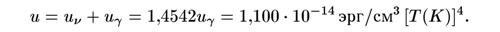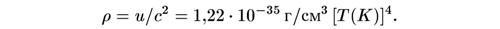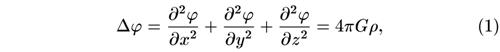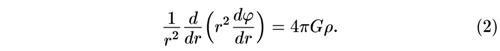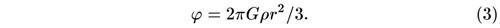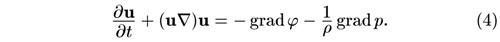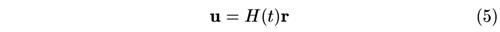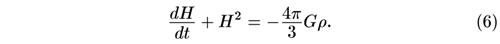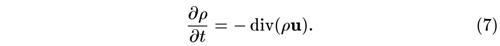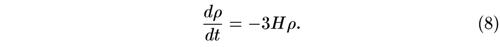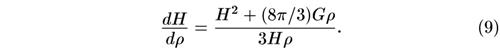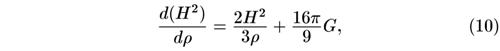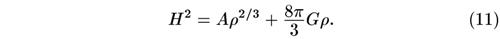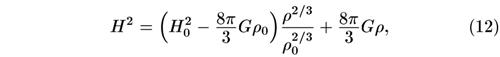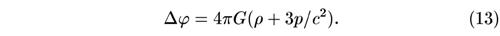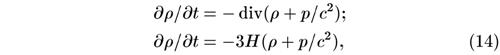Дополнение 6. Плотность и температура нейтрино

 

До тех пор, пока сохраняется тепловое равновесие, полное значение величины, называемой «энтропией», остается фиксированным. В достаточном для наших целей приближении энтропия S в единице объема при температуре Т дается формулой

где NT — эффективное число разновидностей частиц, находящихся в тепловом равновесии, пороговая температура которых ниже Т. Для того чтобы удержать полную энтропию постоянной, S должна быть пропорциональна обратному кубу размера Вселенной. Это значит, что если R есть расстояние между любой парой типичных частиц, то

Как раз перед аннигиляцией электронов и позитронов (при температуре около 5 × 109 К) нейтрино и антинейтрино уже вышли из теплового равновесия с остальным содержимым Вселенной, так что единственными частицами, имевшимися в больших количествах в равновесии, были электрон, позитрон и фотон. Мы видим, что согласно табл. 1 полное эффективное число разновидностей частиц перед аннигиляцией составляло[60]

После аннигиляции электронов и позитронов в четвертом кадре единственными частицами, которые остались в равновесии в большом количестве, были фотоны. Эффективное число разновидностей частиц равнялось поэтому просто

Из закона сохранения энтропии следует, что

Это значит, что тепло, выделившееся при аннигиляции электронов и позитронов, увеличило величину TR на множитель

Перед аннигиляцией электронов и позитронов температура нейтрино Tν была такой же, как и температура фотонов Т. Но после этого Т просто падала как 1/ R, так что для всех последующих моментов времени произведение TνR равнялось значению TR перед аннигиляцией.

Отсюда заключаем, что после окончания процесса аннигиляции температура фотонов оказалась выше температуры нейтрино в

Нейтрино и антинейтрино, даже хотя они и не находятся в тепловом равновесии, дают важный вклад в космическую плотность энергии. Эффективное число разновидностей нейтрино и антинейтрино равно[61]7/2, или 7/4 от эффективного числа разновидностей фотонов. (Имеются два спиновых состояния фотона.) В то же время четвертая степень температуры нейтрино меньше, чем четвертая степень температуры фотонов, на множитель (4/11)4/3. Следовательно, отношение плотности энергии нейтрино и антинейтрино к плотности энергии фотонов

Закон Стефана-Больцмана (см. главу III) утверждает, что при температуре фотонов Т плотность энергии фотонов

Следовательно, полная плотность энергии после электрон-позитронной аннигиляции равна

Мы можем перевести это в эквивалентную плотность массы, разделив на квадрат скорости света, и найдем тогда

 

ДОПОЛНЕНИЯ РЕДАКТОРА РУССКОГО ПЕРЕВОДА

 

ДОПОЛНЕНИЕ 1. КЛАССИЧЕСКАЯ

НЕРЕЛЯТИВИСТСКАЯ КОСМОЛОГИЯ

 

В предлагаемой книге Вайнберг для определения закона расширения Вселенной рассматривает шар, выделенный из безграничной среды. Гравитационное поле среды, окружающей шар, при этом не рассматривается: как известно, поле внутри сферически-симметричной оболочки равно нулю. Вывод Вайнберга правилен. Однако у читателя могут возникнуть сомнения, нет ли произвола в операции мысленного выделения шара[62]. Поэтому полезно дать вывод, также основанный на ньютоновой теории тяготения, в котором искусственное выделение шара не используется. Логическая простота при этом покупается ценой некоторого математического усложнения решения. Приводимый ниже вывод оказывается также весьма полезным в теории образования галактик при рассмотрении возмущений идеального решения. Однако в этом дополнении мы не касаемся вопроса о возмущениях.

Итак, для определения закона расширения будем непосредственно рассматривать безграничную среду, ее гравитационный потенциал и движение.

Уравнение тяготения запишем в форме уравнения Пуассона:

где φ — потенциал гравитационного поля; G — гравитационная постоянная; ρ — плотность. Будем искать сферически-симметричное решение с φ, зависящим только от r = (х2 + у2 + z2)1/2. Тогда

Решение этого уравнения имеет вид:

Мы привыкли к тому, что потенциал равен нулю на бесконечности; для ограниченной совокупности масс это так и есть. В безграничной Вселенной, равномерно заполненной веществом, это не так, однако нет никаких причин отказываться от приведенного решения.

Давление, так же как и плотность, считаем не зависящим от координат. В уравнение движения сплошной среды входит градиент давления, но в данном случае эта величина равна нулю.

Общий вид уравнения движения сплошной среды:

Подставим сюда выражение закона Хаббла

и используем выражение (3) для φ(r) и то, что grad ρ = 0. Сократив r, получим:

Наконец, составим уравнение неразрывности:

Подставив сюда хаббловское выражение скорости (5), найдем, что не зависящая от координат (но зависящая от времени) плотность удовлетворяет уравнению

Система уравнений (6) и (8) полностью эквивалентна тем уравнениям, которые выписаны автором книги в дополнении 2. Для ее решения удобно поделить одно уравнение на другое. Тогда

Это уравнение легко представить в виде линейного уравнения относительно величины H2:

решение которого с заданными (измеренными в настоящее время) значениями Н0 и ρ0 нетрудно записать. Общее решение имеет вид (А — константа интегрирования):

 

я2 = V/3 + YGp- (и)

Подставляя сегодняшние значения Н0 и ρ0 получаем окончательно

что полностью описывает и прошлое (при ρ > ρ0) и будущее Вселенной. Еще одним интегрированием можно найти t(ρ) и тем самым связать Н и ρ с t.

Однако мы не останавливаемся на этом. Нашей целью была демонстрация того, что не нужно искусственно выделять какой-то шар, рассматривать находящуюся на краю точку, делать правдоподобные, но не строгие предположения о том, что внешняя (бесконечная!) область не влияет на движение.

Выше были применены регулярные методы рассмотрения движения сплошной среды и ясные предположения о том, что ищется решение изотропное и однородное, т. е. такое, в котором равноценны все направления и все точки пространства. Изотропия следует из сферически-симметричного вида функции φ и симметрии закона Хаббла. В однородности решения легко убедиться, меняя начало координат и переходя к новой системе, ускоренно движущейся относительно старой. Безграничность среды, так же как и обращение потенциала в бесконечность на пространственной бесконечности, не создает никаких трудностей при расчете[63].

Все расчеты могли бы быть проделаны не только в девятнадцатом, но и в восемнадцатом веке. Тщательный логический анализ понятий однородности и изотропии в ньютоновой механике — вот что могло бы привести к сверхраннему открытию теории расширяющейся Вселенной. Парадокс — один из тех, которыми изобилует наука, — заключается в том, что ньютонова теория космологического расширения была создана лишь после научного подвига Фридмана. Вспоминаются слова Пастернака: «Хоть простота нужнее людям, но сложное доступней им».

За всем сказанным выше не следует, однако, забывать, что релятивистская теория богаче и содержательнее ньютоновой; в общей теории относительности выясняется еще и глобальная геометрия мира.

Наконец заметим, что на ранней стадии мы имеем дело с веществом, давление которого того же порядка, что и плотность энергии покоя ρс2. Газ, состоящий из частиц, движущихся со скоростью света, имеет давление р = ρс2 /3. В этом случае, как нас учит общая и специальная теория относительности, уравнения несколько меняются. Уравнение Пуассона имеет вид:

Поэтому можно сказать, что давление тоже «весит».

Уравнение неразрывности имеет вид:

так как плотность в данном объеме уменьшается не только вследствие вытекания части вещества из данного объема, но и за счет работы расширения, в силу закона эквивалентности массы и энергии.