
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия равновесия пространственной системы сил.Содержание книги
Поиск на нашем сайте
1) Для равновесия произвольной пространственной системы сил необходимо, чтобы главный вектор
2)Для равновесия произвольной пространственной системы сил необходимо, чтобы суммы проекций всех сил на каждую ось и суммы их моментов относительно этих осей были равны нулю.
13. Теорема о моменте равнодействующей силы (теорема Вариньона). Момент равнодействующей относительно некоторой точки О равен сумме моментов, составляющих сил, относительно той же точки. Пусть на тело действует система сил
Центр тяжести твердого тела, плоской фигуры, линии. Центр тяжести – это точка, через которую при любом положении тела проходит линия действия его силы тяжести. Координаты центра тяжести тела могут быть определены по формулам: Если тело представляет собой однородную плоскую и тонкую пластину, то для координат центра тяжести поверхности получаем: Координаты центра тяжести однородной линии:
Основные задачи кинематики. Основные понятия кинематики.
1) установление матем способов задания движения тел в заданной системе отсчета. 2) Опред-е по заданному движению всех основных кинемат-х характеристик (скор,ускорение,траектория) Кинематика – изучаются геометрические св-ва механического движения тел без учета их масс и действующих на них сил. Траектория – линия по корой движется тело. Тело отсчета- тело относительно которого определяется положение тела. Движение тела считается заданным если в любой момент времени известно положение его точек. 16. Векторный способ задания движения точки. Определение скорости и ускорения. Положение точки на траектории определяется радиус вектором относительно этой точки соединяющей начало точки с центром
Скорость- это векторная величина характер-ая быстроту и направление перемещени или движении точки(м/с)
Ускорение-векторная величина хар-ая быстроту и направление изменения скорости.
Поступательное движение твёрдого тела. Поступательное движение тела –движение тела при котором любая прямая,соед-ая 2 любые точки тела перемещается оставаясь // своему начальному положению. Основная теорема: При поступат. движ. тела все его точки в каждый момент времени имеют одинаковые скорости и ускорения, а траектории всех точек при наложении совпадают.
Вращательное движение твёрдого тела. Угловая скорость и угловое ускорение.
Определение скоростей и ускорений точек твёрдого тела вращающегося вокруг неподвижной оси.
Вращ движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными.
22 Сложное движение точки. Основные определения. Примеры.
Сложение скоростей при сложном движении точки.
Сложение ускорений при сложном движении точки.
Ускорение Кориолиса. Численная величина и направление.
Плоскопараллельное движение твёрдого тела.
27. Способы определения скорости точки тела при плоском движении.
Мгновенный центр скоростей. Мгновенный центр скоростей – точка плоской фигуры, скорость которой в данный момент равна нулю – Р. Если тело движется непоступательно, т.е. w¹0, то мгн.цент.ск. всегда существует. При поступательном движении м.ц.с. находится в ¥. 29. Способы определения положения мгновенного центра скоростей
Аксиомы динамики.
Дифференциальные уравнения движения точки. Две задачи динамики.
Первая (прямая) задача динамики. Пример.
Вторая (обратная) задача динамики. Пример.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.139 (0.013 с.) |

 и главный момент
и главный момент  были равны нулю, то есть система приводилась к случаю.
были равны нулю, то есть система приводилась к случаю.
 .
. 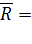 F1+F2+…+Fn
F1+F2+…+Fn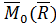 =
= 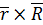 =
=  ×(F1+F2+…+Fn)=
×(F1+F2+…+Fn)= 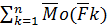
 ;
;  ;
;  , где
, где  ,
,  ,
, 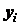 ,
,  - вес и координаты
- вес и координаты  - й частицы тела;
- й частицы тела;  - вес тела.
- вес тела.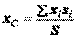 ;
;  ;
; 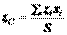 , где
, где  - площадь поверхности.
- площадь поверхности. ;
;  ;
; 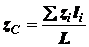 .
.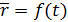 -з-н движения в векторном виде
-з-н движения в векторном виде rx,ry,rz-проекции r на координатные оси
rx,ry,rz-проекции r на координатные оси
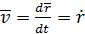
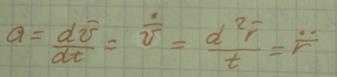








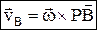 – скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена ^ этому отрезку в сторону вращения фигуры.
– скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена ^ этому отрезку в сторону вращения фигуры. 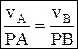 , скорости точек тела пропорциональны их расстояниям до м.ц.с.
, скорости точек тела пропорциональны их расстояниям до м.ц.с. 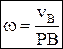 , угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с.
, угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с.







