
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7.1 Система параллельных силСодержание книги
Поиск на нашем сайте
[7.1.1] ВЫБОР Вертикальная сила, интенсивность которой равна массе точки, умноженной на ускорение свободного падения... в- сила трения в- сила инерции в- сила сопротивления в+ сила тяжести
[7.1.2] ВЫБОР Точка тела через которую всегда проходит сила тяжести... в- материальная в- моментная в- начало системы координат в+ центр тяжести
[7.1.3] ВЫБОР Центром тяжести треугольника является точка пересечения... в- биссектрис в- катетов в- высот в+ медиан
[7.1.4] ВЫБОР Координата XС центра тяжести однородного отрезка …
в- L в- 0 в- L/3 в- 2L/3 в+ L/2
[7.1.5] ВЫБОР Координата YС центра тяжести однородного отрезка …
в- L в- 0 в- L/3 в- 2L/3 в+ L/2
[7.1.6] ВЫБОР Расстояние ОС от центра тяжести сектора до его вершины определяется по формуле …
в- в- в- в- в+
[7.1.7] ВЫБОР Координата YС центра тяжести треугольника равна …
в- в- в- в- в+
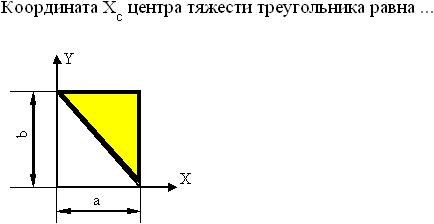
[7.1.8] ВЫБОР Координата XС центра тяжести треугольника равна …
в- в- в- в- в+
[7.1.9] ВЫБОР Координата XС центра тяжести сектора:
в- в- в- в+ в+
[7.1.10] ВЫБОР Координата YС центра тяжести сектора:
в- в- в- в+ в+
[7.1.11] ВЫБОР Координата YС центра тяжести треугольника равна …
в- в- в- в+
[7.1.12] ВЫБОР Координата XС центра тяжести треугольника равна …
в- в- в- в+
[7.1.13] ВЫБОР Расстояние от центра окружности до центра тяжести дуги окружности (ОС) …
в- в- в- в- в+
[7.1.14] ВЫБОР Плоские фигуры состоят из квадратов и прямоугольника из одинакового однородного материала. Соотношение размеров видны из рисунка. Центр тяжести изображенной на рисунке фигуры находится …
в- в площади квадрата В в- в площади квадрата D в- в площади прямоугольника А в+ в площади квадрата С
[7.1.15] ВЫБОР Координата YС центра тяжести дуги окружности …
в- в- в- в- в+
[7.1.16] ВЫБОР Центр тяжести С конуса находится на прямой линии, соединяющей центр окружности О с вершиной пирамиды S. Расстояние ОС от основания конуса до центра тяжести равно …
в- в- в- в+
[7.1.17] ВЫБОР Координата XС центра тяжести сложной фигуры массой М …
в- в- в- в+
[7.1.18] ВЫБОР Координата XС центра тяжести плоской фигуры …
в- в- в- в- в+
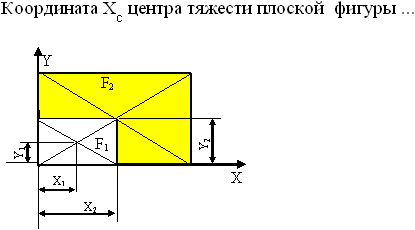
[7.1.19] ВЫБОР Координата YС центра тяжести сложной фигуры массой М …
в- в- в- в+
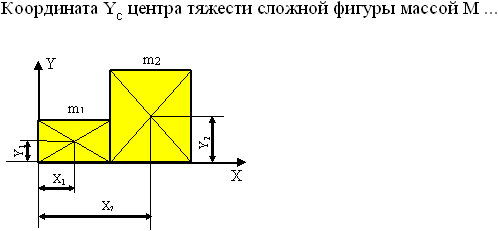
[7.1.20] ВЫБОР Координата YС центра тяжести плоской фигуры …
в- в- в- в+
[7.1.21] ВЫБОР Центр тяжести данной трапеции лежит …
в- ниже оси x в- на оси х в- на пересечении диагонали в+ выше оси х
[7.1.22] ВЫБОР Центр тяжести С пирамиды с квадратным основанием находиться на прямой линии, соединяющей центр квадрата О с вершиной пирамиды S. Расстояние ОС от основания пирамиды до центра тяжести равно …
в- в- в- в+
[7.1.23] ВЫБОР Координата XС центра тяжести дуги окружности…
в- в- в- в- в+
[7.1.24] ВЫБОР Каркас стула изготовлен из однородных стержней одинаковой длины. Центр тяжести изображенной на рисунке фигуры находится …
в- выше плоскости сиденья в- ниже плоскости сиденья, но выше плоскости, проходящей через середины ножек в- ниже плоскости, проходящей через середины ножек в+ в плоскости сиденья
[7.1.25] ВЫБОР У однородной квадратной пластины вырезана четверть. Центр тяжести изображенной на рисунке фигуры находится …
в- в зоне II в- в зоне IV в- в зоне I в+ в зоне III
[7.1.26] ВЫБОР Определить координату zc центра тяжести круглого однородного конуса, если радиус основания R=
в- 0,5 в- 1,25 в- 0,1 в+ 0,75
[7.1.27] ВЫБОР Определить координату yс центра тяжести однородного полукруга радиусом R=0,25м … м
в- 0,18 в- 0,21 в- 0,16 в+ 0,1
[7.1.28] ВЫБОР Определить координату хс центра тяжести однородного полукруга радиусом R=0,5м …
в- 0,31 в- 0,16 в- 0,25 в+ 0,21
[7.1.29] ВЫБОР Определить координату yс центра тяжести однородного сектора радиусом R=0,5м, если φ=1200 … м
в- 0,31 в- 0,24 в- 0,22 в+ 0,28
[7.1.30] ВЫБОР Определить координату yс центра тяжести однородного сектора радиусом R=0,5м, если φ=900 … м
в- 0,22 в- 0,33 в- 0,25 в+ 0,3
[7.1.31] ВЫБОР
Определить координату yс центра тяжести однородного сектора радиусом R=0,5м, если φ=600 … м
в- 0,20 в- 0,38 в- 0,25 в+ 0,32
[7.1.32] ВЫБОР Определить координату zc центра тяжести круглого однородного конуса, если радиус основания R=
в- 0,5 в- 0,45 в- 0,3 в+ 0,25
Раздел 8. Теория трения Тема 8.1 Силы трения [8.1.1] ВЫБОР Груз весом P стоит на негладкой (коэффициент трения скольжения f) поверхности, наклоненной к горизонту под углом a. Сила трения F тр равна… в – F тр = P cos a в – F тр = P sin a в + F тр = f P cos a в – F тр = f P sin a
[8.1.2] ВЫБОР Груз весом P стоит на негладкой (коэффициент трения скольжения f) поверхности, наклоненной к вертикали под углом a. Сила трения F тр равна… в – F тр = P cos a в – F тр = P sin a в – F тр = f P cos a в + F тр = f P sin a
[8.1.3] ВЫБОР Груз весом P стоит на негладкой (коэффициент трения скольжения f) поверхности под действием силы G, наклоненной к вертикали под углом a. Сила трения F тр равна… в – F тр = G cos a в – F тр = G sin a в – F тр = f (P – G cos a) в + F тр = f (P – G sin a)
[8.1.4] ВЫБОР Груз весом P стоит на негладкой (коэффициент трения скольжения f) поверхности под действием силы G, наклоненной к горизонту под углом a. Сила трения F тр равна… в – F тр = G cos a в – F тр = G sin a в – F тр = f (P + G cos a) в + F тр = f (P + G sin a)
[8.1.5] ВЫБОР Груз весом P стоит на негладкой (коэффициент трения скольжения f) поверхности под действием силы G, наклоненной к вертикали под углом a. Сила трения F тр равна… в – F тр = G cos a в – F тр = G sin a в + F тр = f (P + G cos a) в – F тр = f (P + G sin a)
[8.1.6] ВЫБОР Груз весом P стоит на негладкой поверхности под действием силы G, наклоненной к вертикали под углом a. Минимальный коэффициент трения скольжения f, необходимый для равновесия тела, равен … в – f = G cos a /(P + G sin a) в + f = G sin a /(P + G cos a) в – f = G cos a /(P – G sin a) в – f = G sin a /(P – G cos a)
[8.1.7] ВЫБОР Груз весом P стоит на негладкой поверхности под действием силы G, наклоненной к вертикали под углом a. Минимальный коэффициент трения скольжения поверхности f, необходимый для равновесия тела, равен … в – f = G cos a /(P + G sin a) в – f = G sin a /(P + G cos a) в – f = G cos a /(P – G sin a) в + f = G sin a /(P – G cos a)
[8.1.8] ВЫБОР Груз весом P стоит на негладкой поверхности под действием силы G, наклоненной к горизонту под углом a. Минимальный коэффициент трения скольжения f, необходимый для равновесия тела, равен … в + f = G cos a /(P + G sin a) в – f = G sin a /(P + G cos a) в – f = G cos a /(P – G sin a) в – f = G sin a /(P – G cos a)
[8.1.8] ВЫБОР Груз весом P стоит на негладкой поверхности под действием силы G, наклоненной к горизонту под углом a. Минимальный коэффициент трения скольжения f, необходимый для равновесия тела, равен … в – f = G cos a /(P + G sin a) в – f = G sin a /(P + G cos a) в + f = G cos a /(P – G sin a) в – f = G sin a /(P – G cos a)
[8.1.10] ВЫБОР Диск весом P и радиусом R стоит на негладкой поверхности (коэффициент трения качения δ), наклоненной к горизонту под углом a. Максимальное значение угла, при котором равновесие сохраняется … в – α=arcсtg (δ/R) в – α=arcsin (δ/R) в – α=arccos (δ/R) в + α=arctg (δ/R)
[8.1.11] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к горизонту. Момент сопротивления Мс, действующий на диск при равновесии … в – Мс = GR cos a в – Мс = GR sin a в – Мс = δ (P – G cos a) в + Мс = δ (P – G sin a)
[8.1.12] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к вертикали. Момент сопротивления Мс, действующий на диск при равновесии … в – Мс = GR cos a в – Мс = GR sin a в + Мс = δ (P – G cos a) в – Мс = δ (P – G sin a)
[8.1.13] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к горизонту. Момент сопротивления Мс, действующий на диск при равновесии … в – Мс = GR cos a в – Мс = GR sin a в – Мс = δ (P + G cos a) в + Мс = δ (P + G sin a)
[8.1.14] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к вертикали. Момент сопротивления Мс, действующий на диск при равновесии … в – Мс = GR cos a в – Мс = GR sin a в + Мс = δ (P + G cos a) в – Мс = δ (P + G sin a)
[8.1.15] ВЫБОР Диск весом P и радиусом R стоит на негладкой поверхности (коэффициент трения качения δ), наклоненной к горизонту под углом a. Условие равновесия диска имеет вид … в – Psinα δ= PR cos a в – Pδ = PR sin a в – Pcosα δ = PR в + Psinα R= Pδ cos a
[8.1.16] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к горизонту. Условие равновесия диска имеет вид … в – Psinα δ= GR cos a в – (P+Gcosα)δ = GR sin a в – (P−Gcosα)δ = GR sin a в – (P+Gsinα)δ = GR cos a в + (P−Gsinα)δ = GR cos a
[8.1.17] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к вертикали. Условие равновесия диска имеет вид … в – P δ= GR cos a в – (P+Gcosα)δ = GR sin a в + (P−Gcosα)δ = GR sin a в – (P+Gsinα)δ = GR cos a в − (P−Gsinα)δ = GR cos a
[8.1.18] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к горизонту. Условие равновесия диска имеет вид … в – P δ= GR cos a в – (P+Gcosα)δ = GR sin a в − (P−Gcosα)δ = GR sin a в + (P+Gsinα)δ = GR cos a в − (P−Gsinα)δ = GR cos a
[8.1.18] ВЫБОР Диск весом P и радиусом R стоит на негладкой горизонтальной поверхности (коэффициент трения качения δ). На диск действует сила G, наклоненная под углом α к вертикали. Условие равновесия диска имеет вид … в – P δ= GR cos a в + (P+Gcosα)δ = GR sin a в − (P−Gcosα)δ = GR sin a в − (P+Gsinα)δ = GR cos a в − (P−Gsinα)δ = GR cos a
[8.1.20] ВЫБОР Тело весом P находится в покое на негладкой поверхности, наклоненной к горизонту под углом α. К телу приложена сила F, направленная вдоль поверхности. Сила трения F тр равна … в – F тр = P cos a+F в – F тр = P sin a+F в − F тр = P cos a−F в + F тр = P sin a − F
[8.1.21] ВЫБОР Тело весом P находится в покое на негладкой поверхности (коэффициент трения скольжения f), наклоненной к горизонту под углом α. К телу приложена сила F, направленная вдоль поверхности. Условие равновесия тела имеет вид … в – f Psin α = P cosa+F в – f Pcosα = P sina+F в − + f Psinα =P cos a−F в + f Pcosα = P sina − F
[8.1.22] ВЫБОР Тело весом P находится в покое на негладкой поверхности (коэффициент трения скольжения f), наклоненной к горизонту под углом α. К телу приложена сила F, направленная вдоль поверхности. Минимальный коэффициент трения скольжения f, необходимый для равновесия тела, равен … в – f = (P cosa+F)/ Psin α в – f = (P sina+F)/ Pcosα в − + f = (P cos a− F)/ Psinα в + f = (P sina − F)/ Pcosα
[8.1.23] ВЫБОР Тело весом P находится в покое на негладкой поверхности, наклоненной к горизонту под углом α. На тело действует горизонтальная сила F. Сила трения F тр равна … в – F тр = P cosa+Fcosα в – F тр = P sina+Fsinα в − F тр = P cosa−Fsinα в + F тр = P sina − Fcosα
[8.1.24] ВЫБОР Тело весом P находится в покое на негладкой поверхности (коэффициент трения скольжения f), наклоненной к горизонту под углом α. На тело действует горизонтальная сила F. Условие равновесия тела имеет вид … в – f (P sina+Fsinα) = P cosa+Fcosα в – f (P cosa+Fcosα) = P sina+Fsinα в − f (P sina+Fsinα) = P cosa−Fsinα в + f (P cosa+Fcosα) = P sina − Fcosα
[8.1.25] ВЫБОР Тело весом P находится в покое на негладкой поверхности, наклоненной к горизонту под углом α. На тело действует горизонтальная сила F. Минимальный коэффициент трения скольжения f, необходимый для равновесия тела, равен … в – f = (P cosa+Fcosα)/ (P sina+Fsinα) в – f = (P sina+Fsinα)/(P cosa+Fcosα) в − f = (P cosa−Fsinα)/(P sina+Fsinα) в + f = (P sina − Fcosα)/(P cosa+Fcosα)
[8.1.26] ВЫБОР Тело весом P находится в покое на негладкой поверхности, наклоненной к горизонту под углом α. На тело действует горизонтальная сила F. Сила трения F тр равна … в + F тр = P cosa+Fcosα в – F тр = P sina+Fsinα в − F тр = P cosa−Fsinα в − F тр = P sina − Fcosα
[8.1.27] ВЫБОР Тело весом P находится в покое на негладкой поверхности (коэффициент трения скольжения f), наклоненной к горизонту под углом α. На тело действует горизонтальная сила F. Условие равновесия тела имеет вид … в + f (P cosa−Fsinα) = P sina+Fcosα в – f (P sina+Fcosα) = P sina+Fsinα в − f (P sina−Fsinα) = P cosa−Fsinα в − f (P cosa+Fcosα) = P sina − Fcosα
[8.1.28] ВЫБОР Тело весом P находится в покое на негладкой поверхности, наклоненной к горизонту под углом α. На тело действует горизонтальная сила F. Минимальный коэффициент трения скольжения f, необходимый для равновесия тела, равен … в – f = (P sina+Fcosα)/ (P sina+Fsinα) в – f = (P sina+Fsinα)/(P cosa−Fcosα) в − f = (P cosa−Fsinα)/(P sina+Fsinα) в + f = (P sina+Fcosα)/(P cosa−Fsinα)
[8.1.29] ВЫБОР Тело весом P находится на негладкой горизонтальной поверхности (коэффициент трения скольжения f). К телу приложена сила F, направленная под углом α к горизонтальной поверхности. Минимальный вес тела P, при котором возможно его равновесие, равен … в- в- в- в- в+
[8.1.30] ВЫБОР Тело весом P находится на негладкой горизонтальной поверхности. К телу приложена сила F, направленная под углом α к горизонтальной поверхности. Минимальный вес тела P, при котором возможно его равновесие, равен … в- в- в- в- в+
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.1.23 (0.008 с.) |













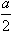












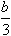



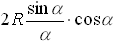


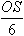
























 м, α= 300 … м
м, α= 300 … м







