Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класифікація подій. Класичне поняття ймовірності (комбінаторна ймовірність).Содержание книги
Поиск на нашем сайте
Класифікація подій. Класичне поняття ймовірності (комбінаторна ймовірність). · Випадкова (стохастична) подія – якщо при певній сукупності умов вона може відбутись, а може і не відбутись. · Масова подія – сукупність умов, які її породжують можна повторити безліч раз. · Протилежна подія до події A полягає в тому. що подія А не відбувається. · Об’єднання (сума) подій A і B – подія яка полягає в тому, що відбувається або А, або В, або А і В одночасно. Позначається · Суміщення (добуток) подій A і B – подія яка полягає в тому, що відбувається і А, і В одночасно. Позначається · Еквівалентні події – якщо поява кожної з них супроводжується появою іншої.
· Несумісні – якщо їх добуток є неможливою подією.
Повна система подій – якщо вони попарно несумісні, а в об’єднанні – вірогідна подія. Події A1,A2,…,An називаються сприятливими для події А, якщо вони попарно несумісні, а їх об’єднання дає подію А. Якщо рівноможливі події Е1,Е2, …, En утворюють повну сукупність несумісних події, і з них деякі є сприятливими для події А, то ймовірністю події А є відношення кількості сприятливих для А подій до кількості подій в повній сукупності. Теореми про ймовірність суми подій. Т. Ймовірність появи несумісних подій дорівнює сумі ймовірностей цих подій: P(A+B) = P(A) + P(B), якщо A*B=V Доведення: Нехай повна сукупність рівно можливих несумісних подій складається з n елементарних подій. Нехай A розпадається на k сприятливих подій, B – на m сприятливих подій. Оскільки А і В несумісні, то немає подій, які сприятливі для A i B одночасно. Тому P(A+B) = (k + m)/n = k/n + m/n = P(A) + P(B).
Т. Ймовірність суми двох подій рівна сумі їх ймовірностей мінус ймовірність їх суміщення. P(A+B) = P(A) + P(B) – P(A*B) Доведення: з діаграм Вена. (або алгебраїчно через суму несумісних) Умовні ймовірності (ймовірності добутку подій) Якщо ймовірність виконання події А залежить від виконання іншої події В, то ймовірність появи події А в цьому випадку називається умовною ймовірністю. P(A/B) – ймовірність події А, за умови, що відбулась подія В.
Т. Ймовірність добутку двох подій рівна добутку ймовірності однієї на умовну ймовірність другої, за умови, що відбулась перша: P(A*B) = P(A)* P(A/B) = P(B)* P(B/A) Доведення: Нехай події E1,E2,…,En утворюють повну сукупність рівноможливих подій, з яких r сприятливі для A, s – для B, m – для А і В одночасно. Тоді
P(A*B) = m/n = (m/s) * (s/n) = P(B)*P(B/A) P(A*B) = m/n = (m/r) * (r/n) = P(A)*P(A/B). Незалежні події Якщо подія А не змінює ні сукупності умов S, ні сприятливих подій для події B, то подія B називається незалежною від події А. Формальніше можна сказати так: Подія А незалежна від події В, якщо P(A/B) = P(A). Аналогічно: подія В незалежна від події А, якщо P(В/А) = P(В).
Отже, з теореми про добуток подій отримуємо, що для незалежних подій P(A*B) = P(A)*P(B). Т. Якщо подія А не залежить від події В, то і подія В не залежить від події А. Доведення: Якщо P(A/B) = P(A), то P(A*B) = P(B) * P(A/B) = P(A)*P(B) = P(A)*P(B/A) => P(B) = P(B/A) => B не залежить від А. Незалежні в сукупності події Якщо подій більше двох, то вони можуть бути попарно залежні, незалежні, можуть зустрічатись ті чи інші види залежності в підмножинах подій.
Події А1,А2,…,An називаються незалежні в сукупності, якщо для будь-якої підмножини їх Ai1, Ai2, …, Aik виконується P(Ai1* Ai2*…* Aik) = P(Ai1) * P(Ai2) * … * P(Aik).
Це означає, що події можуть бути попарно незалежні, а в сукупності – ні. Формула повної ймовірності Повна сукупність несумісних подій – якщо вони попарно несумісні і хоча б одна з них точно відбувається.
Т. Нехай задана повна сукупність несумісних подій H1,H2,…,Hn, і подія А може відбутись лише в парі з однією з цих подій. Тобто: А = H1*A + H2*A + … + Hn*A. Тоді H1,H2,…,Hn називаються гіпотезами, а ймовірність події А обчислюється так:
Доведення: Якщо події H1,H2,…,Hn попарно несумісні, то попарно несумісні будуть і події Hi*A (i=1..n). Тому з теореми про добуток несумісних подій маємо:
а з теореми про ймовірність залежних подій:
Це і є формула повної ймовірності. 7. Формула гіпотез (формула Байєса) Нехай задана повна сукупність несумісних подій H1,H2,…,Hn, і подія А може відбутись лише в парі з однією з цих подій. Тобто: А = H1*A + H2*A + … + Hn*A. Тоді H1,H2,…,Hn називаються гіпотезами. Нехай тепер відомо, що подія А відбулась, обчислимо P(Hi/A), тобто уточнити ймовірності гіпотез, виходячи з того факту, що подія А відбулась.
З теореми про ймовірність залежних подій маємо:
Звідси, і з формули повної ймовірності отримуємо:
Остання формула і називається формулою Байєса. Ймовірності P(Hi) називаються апріорні, а P(Hi/A) – апостеріорні.
Біномний розподіл Фіксований набір чисел (ймовірностей), сума яких = 1 називають розподілом ймовірностей. Якщо маємо схему Бернуллі, то для чисел s=0..n можемо поставити у відповідність ймовірності появи s подій А у n спробах.
З формули біному Ньютона маємо:
Оскільки p+q = 1, то ми отримали розподіл ймовірностей. Цей розподіл називається біномним розподілом.
Аналогічно можна отримати і від’ємнобіномний розподіл, якщо числам m=1..n поставити у відповідність ймовірності того, що подія А у n-ій спробі з’явилась m-ий раз:
Теорема Пуасона Локальна теорема Муавра-Лапласа дає досить зручне наближення для b(s,n,p). Але, при p близьких до 0 або 1 вона дає значну похибку. Тому краще використовувати наближення Пуасона:
Т. Нехай 0<p<1, n*p = L, тоді Доведення: з формули Бернуллі:
Класи випадкових змінних Випадкова змінна наз. дискретною, якщо множина значень, які вона приймає зліченна, або скінченна. Випадкова змінна наз. абсолютно неперервною, якщо її функція розподілу має вигляд
Властивості густини розподілу: · p(x)>=0 · P(a<t<=b) = int(x=a..b) {p(x)dx} · int(x=-INF..INF) {p(x)dx} = 1 · p(-INF)=p(INF)=0 Пуасонівський процес. Нехай деяка система може перебувати в деяких станах Е1,Е2, …, Ek, причому, якщо в деякий момент часу t вона перебуває в стані Ek, то за час ∆t вона буде перебувати в стані E(k+1) з ймовірністю L*∆t + o(∆t), L>0 (L=const). З імовірністю 1- L*∆t + o(∆t) вона залишиться в стані Ek, і з ймовірностями o(∆t) вона перейде в інші стани. В початковий момент часу вона знаходиться в стані 0. Цей процес можна зобразити наступним графом:
Щоб побудувати модель процесу перейдемо до границі при ∆t -> 0, отримаємо:
Розв’язавши цю задачу Коші, отримаємо Таким чином ми знайшли розподіл ймовірностей перебування системи в стані k в час t. Моменти випадкової змінної Моментом мінливої величини, або статистичним моментом порядку k відносно константи с називається величина
При с=0 момент називається початковим, а при с=середнє вибіркове – центральним. Критерій Смирнова. Критерій Смирнова використовується для того, щоб перевірити, чи вибірки x1,…,xn з абсолютно неперервної популяції X i y1,…,yn з абсолютно неперервної популяції Y мають однакові функції розподілу. Знайдемо емпіричні функції розподілу для вибірок x1,…,xn і y1,..,yn. Тоді розглянемо статистику Смирнов довів, що статистика sqrt(m*n/(m+n))*D при n,m->INF має розподіл Колмогорова. Гіпотеза про медіану. Критерій знаків можна використати для перевірки гіпотези про медіану генеральної сукупності: Me=a. Для цього потрібно утворити пари (x1,a),…,(xn,a). Тоді з означення медіани різниці xi-a повинні бути однаково часто додатніми і від’ємними. Отже, висновки про прийом гіпотези здійснюємо на основі критерію знаків. Критерій Вілкоксона. Критерій Вілкоксона використовується для того, щоб перевірити, чи вибірки x1,…,xn з спостережень над змінною X i y1,…,yn з спостережень над змінною Y мають однакові функції розподілу. Ідея критерію полягає в тому, що якщо змінні однаково розподілені, то на проміжку, де зустрічається деяке число елементів варіаційного ряду першої вибірки, повинно зустрічатись близьке значення елментів варіаційного ряду другої вибірки. Отже виберемо за критерій кількість інверсій однієї вибірки відносно елементів іншої. Тут під інверсією елемента з вибірки розуміється кількість елементів з іншої вибірки, менших за нього. При великих значеннях об’єму вибірок статистика інверсій стає практично нормально розподіленою, а тому з великою точністю можна вважати, що областю прийому гіпотези є
Пряма регресія. Нехай маємо n пар незалежних спостережень проведених в однакових умовах над двовимірним вектором (X,Y). Випадкові змінні X,Y нам не відомі, але на основі знайдених значень хочемо зробити висновок про кореляцію між ними.
Кореляції вищих порядків.
Класифікація подій. Класичне поняття ймовірності (комбінаторна ймовірність). · Випадкова (стохастична) подія – якщо при певній сукупності умов вона може відбутись, а може і не відбутись. · Масова подія – сукупність умов, які її породжують можна повторити безліч раз. · Протилежна подія до події A полягає в тому. що подія А не відбувається. · Об’єднання (сума) подій A і B – подія яка полягає в тому, що відбувається або А, або В, або А і В одночасно. Позначається · Суміщення (добуток) подій A і B – подія яка полягає в тому, що відбувається і А, і В одночасно. Позначається · Еквівалентні події – якщо поява кожної з них супроводжується появою іншої.
· Несумісні – якщо їх добуток є неможливою подією.
Повна система подій – якщо вони попарно несумісні, а в об’єднанні – вірогідна подія. Події A1,A2,…,An називаються сприятливими для події А, якщо вони попарно несумісні, а їх об’єднання дає подію А. Якщо рівноможливі події Е1,Е2, …, En утворюють повну сукупність несумісних події, і з них деякі є сприятливими для події А, то ймовірністю події А є відношення кількості сприятливих для А подій до кількості подій в повній сукупності.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.142.168 (0.009 с.) |

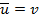
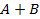 ,
, 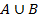 .
. ,
, 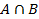 .
.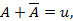

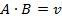

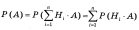

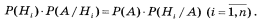

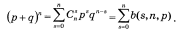
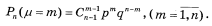

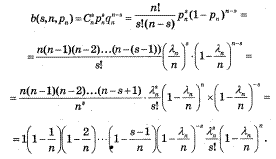 Перейшовши до границі, при n -> INF, маємо, що
Перейшовши до границі, при n -> INF, маємо, що 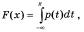 тут p(t) – щільність розподілу.
тут p(t) – щільність розподілу.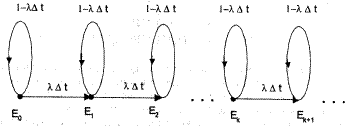

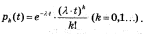


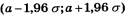 .
.