Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перечень условных обозначений, символов, сокращений и терминовСодержание книги
Поиск на нашем сайте
Перечень условных обозначений, символов, сокращений и терминов
ВВЕДЕНИЕ Известно, что многие экономические объекты при формализации с целью моделирования функционирования допускают применение оптимизационных методов. При этом, широкий класс таких методов укладывается в рамки линейно-программных задач. Такие задачи на формальном уровне состоят в минимизации или максимизации целевой функции при линейных ограничениях. Актуальность темы дипломной работы состоит в том, что любая реальная экономическая задача не исчерпывается одним критерием и при планировании производственных процессов на предприятии необходимо постоянно принимать непростые решения, связанные с учетом многих критериев качества и ограничений на ресурсы. Предмет исследования – оптимизация производство по выпуску продукции на основе математико-экономическую модель косметической предприятии Nature Republic. Объект исследования – оптимизация производство по выпуску продукции на предприятии. Целью является изучение методы многокритериальной оптимизации, современные программные средства поддержки принятия решений MATLAB, а также формулирование экономическую модель и применения методов решения и пакета оптимизации к этой модели. Для достижения цели дипломной работы поставлены следующие задачи: - рассмотреть основные понятия, принципы, структуру и особенности многокритериальной оптимизации линейного программирования; - исследовать систему производства на исследуемом предприятии; - оптимизировать задачу о производстве на основе изученных методов и с помощью инструментального пакета MATLAB; - на основе данных анализа, разработать практические рекомендации по оптимизации производства предприятии Nature Republic. Информационной базой исследования явились положения и концепции, представленные в работах отечественных и зарубежных авторов. Исследование проводилось на основе системно-функционального, комплексного научных подходов, с помощью научных методов: свертывания критериев, главного критерия, последовательных уступок. Данная дипломная работа посвящена изучению методов оптимизации и практическому применению пакетов оптимизации для решения задач многокритериальной линейной оптимизации.
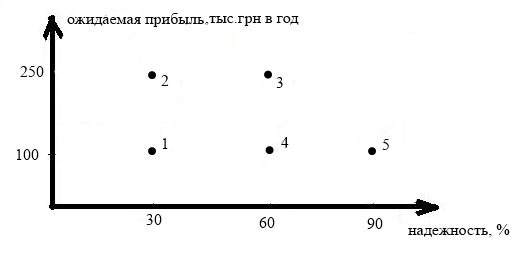
Линейное программирование В настоящее время оптимизация практически неотъемлемая часть в науке, технике, экономике и в любой другой области человеческой деятельности. Оптимизация – целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях [44,46]. Поиски оптимальных решений привели к созданию специальных математических методов и уже в XVIII веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др.) [45,48]. Однако до второй половины XX века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев – невозможно [46]. В зависимости от своей постановки, любая из задач оптимизации может решаться различными методами, и наоборот – любой метод может применяться для решения многих задач. Методы оптимизации могут быть: 1) скалярными (оптимизация проводится по одному критерию); 2) векторными (оптимизация проводится по многим критериям); 3) поисковыми (включают методы регулярного и методы случайного поиска), аналитическими (методы дифференциального исчисления, методы вариационного исчисления и др.); 4) вычислительными (основаны на математическом программировании, которое может быть линейным, нелинейным, дискретным, динамическим, стохастическим, эвристическим и т.д.); 5) теоретико-вероятностными, теоретико-игровыми и др. [45,46,48]. Наиболее часто используемым методом оптимизации является линейное программирование. Линейное программирование (ЛП) – один из первых и наиболее подробно изученных разделов математического программирования [4,29]. Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Леонида Витальевича Канторовича «Математические методы организации и планирования производства». Поскольку методы, изложенные Л.В. Канторовичем, были мало пригодны для ручного подсчета, а быстродействующих вычислительных машин в то время не существовало, работа Л.В. Канторовича осталась почти незамеченной [15,18]. В 50-е гг. ХХ века независимо от Канторовича метод решения задачи линейного программирования (так называемый симплекс-метод) был развит американским математиком Дж. Данцигом, который в 1951 г. и ввел термин «линейное программирование». Можно сказать, свое второе рождение линейное программирование получило с появлением электронно-вычислительных машин (ЭВМ). В то время началось всеобщее увлечение линейным программированием, вызвавшее в свою очередь развитие других разделов математического программирования [29,32]. Слово «программирование» объясняют тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно определяют программу (план) действий некоторого объекта, например, промышленного предприятия. Слово «линейное» отражает линейную зависимость между переменными [12,18]. Линейное программирование находит широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем [4,17]. Многие распространённые классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования. Несмотря на различные области приложения, данные задачи имеют единую постановку [2,12,18]. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: 1) рационального использования сырья и материалов, задачи оптимизации раскроя; 2) оптимизации производственной программы предприятий; 3) оптимального размещения и концентрации производства; 4) составления оптимального плана перевозок, работы транспорта; 5) управления производственными запасами и многие другие, принадлежащие сфере оптимального планирования [4,12,18,29]. Так, по оценкам американских экспертов, около 75% от общего числа применяемых оптимизационных методов приходится на линейное программирование. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций [4]. В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения [32]. Примеры многокритериальности в экономике Как ранее говорилось, в задачах математического программирования с одним критерием нужно определить значение целевой функции, соответствующее, например, минимальным затратам или максимальной прибыли. Однако, немного подумав, можно сказать, что практически в любой реальной ситуации обнаружим несколько целей, противоречащих друг другу [51]. Ниже будет показано, насколько широк диапазон проблем, которые могут быть адекватно сформулированы как многокритериальные, и какие характеристики следует использовать в качестве критериев. 1. Планирование производства: 2. Выбор портфеля ценных бумаг: 3. Составление сметы капиталовложений: – min – спрос на капитальные вложения, ежегодные эксплуатационные расходы. 4. Управление лесным хозяйством: 5. Управление попусками водохранилищ: – min – недопоставки воды на коммунальные нужды в бассейне реки. 6. Формирование ревизионной службы в фирме: 7. Транспортировка: – min – стоимость, среднее время доставки грузов приоритетным клиентам, расход топлива. Конечно, решения, которое одновременно удовлетворяло бы всем противоречивым требованиям, как правило, не существует. Но математика может помочь и при решении таких задач. Помощь эта состоит не в нахождении несуществующего решения, одновременно обращающего все критерии в максимум, а в отбрасывании заведомо плохих решений [28,37,51]. Оптимизация по Парето Впервые проблему многокритериальной оптимизации рассмотрел итальянский экономист Вильфредо Парето в 1904 г. при математическом исследовании товарного обмена [37]. В дальнейшем интерес к проблеме многокритериальной оптимизации усилился в связи с разработкой и использованием вычислительной техники, и уже позднее стало ясно, что многокритериальные задачи возникают также и в технике, например, при проектировании сложных технических систем [51]. Согласно его концепции, общество находится в состоянии общего экономического равновесия и социальной эффективности распределения ресурсов, которое предполагает оптимальное распределение в сфере производства при минимальном использовании ресурсов и эффективное распределение в сфере потребления, обеспечивающее максимум удовлетворения потребностей. В. Парето считал, что в основе анализа общего равновесия должны лежать факты выбора потребителя, когда фиксируется лишь порядок предпочтения одного набора благ перед другими [36,37]. При решении большого числа практических задач приходится сталкиваться с необходимостью нахождения решений, удовлетворяющих нескольким, зачастую конфликтующим между собой, критериям. В связи с этим, решение задачи заключается не в нахождении какого-то одного решения, а в отыскании некоторого множества решений, каждое их которых будет превосходить другие хотя бы по одному критерию. Такие решения, как правило, называются оптимальными по Парето [36]. Необходимость отыскания целого множества решений чрезвычайно усложняет задачу оптимизации и делает практически непригодными большинство классических методов оптимизации. Задача усложняется еще и тем, что надо не только найти решения, максимально близкие к истинному множеству (или фронту) Парето, но и обеспечить максимально возможное различие между такими решениями (т.е. охватить возможно большую часть этого фронта). Принципы многокритериальной оптимизации существенно отличаются от обычной оптимизации. Во втором случае (один критерий) целью решения задачи является нахождение глобального оптимального решения, дающего оптимальное значение для одной целевой функции. В случае нескольких критериев мы имеем соответственно несколько целевых функций, каждая из которых может иметь оптимальное значение при своем собственном наборе значений независимых переменных [28,37]. Если оптимальные решения для различных целевых функций существенно различны, то невозможно говорить об оптимальном решении всей задачи в целом. В этом случае мы получаем множество оптимальных решений, ни одно из которых не является оптимальным по сравнению с другими во всех смыслах (т.е. по все критериям). Это множество называют множеством решений оптимальных по Парето. Проиллюстрируем это на примере, где нужно выбрать стратегию развития предприятия, критерии - ожидаемая прибыль в год (в смысле мат. ожидания из теории вероятностей), надёжность стратегии (вероятность того, что будет приемлемая для нас прибыль, хоть сколько-нибудь солидный доход) [37]. Допустим, у нас есть 5 стратегий:
Рис. 1.2. График оптимального плана развития предприятий Стратегия 2 в среднем даёт больше прибыли, чем стратегия 1, при той же надёжности. Стало быть, стратегия 1 не может быть лучшей. Стратегия 3 по ожидаемой прибыли равноценна стратегии 2, но надёжнее. Стало быть, стратегия 2 тоже невыгодна. Стратегия 3 прибыльнее стратегии 4 при той же надёжность, то есть стратегия 4 тоже неоправданно. Остаются только стратегии 3 и 5. По одному критерию превосходит одна, по другому - другая. Операции, оптимальные по Парето, не обязательно являются «самыми лучшими» - эти операции не являются худшими. Чтобы выбрать конкретное решение из Парето-оптимального множества, нужны дополнительные данные [21]. Выделение множества Парето ещё не даёт ответа на вопрос, какое решение оптимальное, но оно значительно упрощает применение алгоритмов, работающих с дополнительной информацией, поскольку сужает множество возможных вариантов [37,51]. В настоящее время линейная оптимизация является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения.
Метод главного критерия Этот метод предполагает сведения задачи многокритериальной оптимизации к однокритериальной оптимизации. Для этого выбираем один из рассматриваемых критериев в качестве главного критерия, а остальные преобразовываются в ограничения [21]. В качестве главного критерия в различных областях часто выбирают: 1. Себестоимость 2. Объем производства 3. Производительность 4. Ресурсоемкость (металлоемкость, энергоемкость,...) 5. Сроки выполнения работы и др. Задача оптимизации в этом случае, можно сформулировать следующим образом. Вначале нужно задать главный критерий
При этом все значении Х должны принадлежать рассматриваемому допустимому множеству. Наиболее часто этот способ употребляется в инженерной практике. Преимущества метода главного критерия относятся простота интерпретации результатов, отсутствия высоких требований к математической подготовке экспертов, программному обеспечению и вычислительным средствам [51]. После того, как мы сведем задачу многокритериальной оптимизации к задаче однокритериальной оптимизации, мы получаем возможность использовать стандартные программные средства, в частности, такие как поиск решения в Microsoft Excel. К основным недостатком метода относятся: 1) чрезмерное упрощение структуры задач; 2) не всегда можно выделить ярко выраженный главный критерий, иногда это сделать трудно или вообще нельзя; 3) возможность потери эффекта совокупного влияния нескольких второстепенных критериев; 4) ограничения для остальных критериев должны быть обоснованными, а не взяты кое-как; 5) возможность получения неэффективных решений; 6) даже если есть критерий, который гораздо важнее любого другого, то не факт, что в сумме остальные критерии не окажутся весьма значимыми. Особо ярко это может проявляться в задачах, где n велико [21,25,30,33,46]. В методе главного критерия, если задача имеет единственное допустимое решение, то оно является эффективным по Парето. Если же задача имеет более чем одно допустимое решение, то множество этих решений содержит эффективные по Парето решения [37,45,48,51]. Но оно также может содержать и слабо эффективные решения. В связи с этим процедура поиска решения в общем случае включает два этапа: 1) нахождение множества допустимых решений; 2) выбор некоторого эффективного по Парето решения. На практике, критерии очень часто имеют различные масштабы и шкал измерения, и тогда возникает необходимость нормировки этих критериев. Нормировка критериев Для приведения критериев к сопоставимому виду и обеспечения их эквивалентности используется нормировка:
при От значения критерия отнимаем минимальное значение этого критерия и делим полученную разность на разность между максимальным и минимальным значениями этого критерия [51]. Предполагается при этом, что минимальное и максимальное значение не совпадают. При такой нормировке, все нормированные значение Рассмотрим в качестве примера такую задачу, предполагается, что необходимо организовать рекламную компанию по продвижению нового товара. Для этого могут быть использованы альтернативы Исходные данные записываются таким образом:
Прежде чем решить задачу, нужно провести нормировку критериев. В качестве главного критерия берем критерию
Можно зафиксировать постоянные значения, т.е. это максимумы и минимумы у второго и третьего критерия, затем воспользоваться автозаполнением для быстроты работы. В результате получим вот такую таблицу, значения критерия
рис.2.9. Нормировка критериев Выберем такое ограничение, что частные критерия
рис. 2.10. Окончательный результат решения по методу главного критерия Тогда этим ограничениям для критерия Для сравнения, возьмем в качестве ограничение 0,8 умноженное на максимальное значение критериев
Метод свертывания критериев Метод свертывания критериев предполагает преобразование набора имеющихся частных критериев в один суперкритерий.
Т.е. мы получаем новый суперкритерий F, который является функций К основным этапом свертывания относятся: 1. Обоснование допустимости свертки При обосновании допустимости свертки, мы в первую очередь должны подтвердить, что критерии, которые мы сворачиваем, должны быть однородными. Выделяют такие группы показателей эффективности; - показатели результативности; - показатели ресурсоемкости; - показатели оперативности. Критерии, которые мы сворачиваем, должны относиться к одной и той же группе, нельзя сворачивать критерии, которые относятся, например, один из них к показателям оперативности, а другой к показателям результативности. Т.е. для каждой группы свертывание частных критериев следует выполнять отдельно. При нарушении этого принципа теряется смысл критерия [30,33,51]. 2. Нормировка критериев Правила нормализации критериев, мы рассматривали ранее в предыдущем разделе. 3. Учет приоритетов критериев Учет приоритетов обычно задается некоторым векторам весовых коэффициентов, которые отображают важность того или иного критерия для решаемой задачи. 4. Построение функции свертки Для свертывания критериев, используют такие основные типы функций: - Аддитивные функции свертки; - Мультипликативные; - Агрегированные, а также могут быть другие варианты сверток. Аддитивная свертка Аддитивную свертку критериев можно рассматривать как реализацию принципа справедливой компенсации абсолютных значений нормированных частных критериев [25,30,51]. В этом случае, суперкритерий обычно строятся как взвешенная сумма частных критериев
Весовые коэффициенты таблица 2.1. Таблица относительной важности критериев
Мультипликативная свертка Мультипликативная свертка базируется на принципе справедливой компенсации относительных изменений частных критериев. При этом, суперкритерий имеет вид: При использовании мультипликативных критериев не требуется нормировка частных критериев, и это является их преимуществом [30,33,45,46,48]. Выбор между аддитивными и мультипликативными критериями определяется важностью учета абсолютных или относительных изменений значений частных критериев. Агрегирование частных критериев используют также различные варианты агрегирование. В частности, если компенсация значений одних показателей эффективности другими недопустима, то используют функции агрегирования вида:
Для каждого частного критерия, находится его нормированное значение и умножается на весовой коэффициент. А потом из всех полученных величин выбирается либо максимальное, либо минимальное значение. Если первые m показателей надо увеличить, а остальные – уменьшить, то используют функцию агрегирования вида:
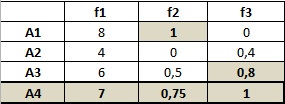
В числители находятся произведение тех критериев, значение которых нам надо максимизировать, а в знаменателе находятся произведение тех критериев, значение которых нам надо минимизировать. И поэтому мы получаем новый критерий, который нам надо будет максимизировать [1,6,9,48,51]. Методы свертывания критериев широко используются в решение задач многокритериальной оптимизации. Однако они имеют также проблемы и недостатки. В частности трудно обосновать выбор метода свертывания критериев, а от выбора метода часто зависит получаемый результат. Другим недостатком является трудность обоснование выбора весовых коэффициентов, часто для этого привлекается эксперты, проводятся опросы, потом обрабатываются полученные результаты, однако это требует много времени и затраты других ресурсов. Еще одна проблема связана с тем, что эти методы, как правила дает возможность компенсировать малые значения одних критериев большими значениями других, что часто бывает неприемлемо для конкретных решений [8,16,21,25]. Рассмотрим в качестве примера такую задачу:
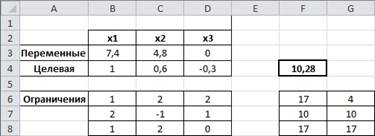
Перед тем как преобразовывать эти критерии в 1, мы должны привести их в однородном состоянии. Т.е. в данном случае нужно максимизировать f2→ f2' = -f2. И тогда получим: Также нужно учитывать и весовые коэффициенты, при этом их сумма должна быть = 1, и каждый из весовых коэффициентов должен быть неотрицательной величиной. Весовые коэффициенты распределяется по важности этих самих частных критериев После подсчета вместе с весовыми коэффициентами, мы получим целевую функцию такого вида: Открываем электронную книгу Excel и, как и для решения однокритериальной задачи определяем ячейки под переменные
рис.2.11. Определение переменных, целевых и ограничений В четвертой строке задаем целевую функцию. В А4 вводим подпись «Целевая», а в В4, С4, D4 наши значения. Дальше, в ячейку F4 вводим формулу «=B4*B3+C4*C3+D4*D3», таким образом, задаем целевую функцию В ячейку F6, F7 и F8 вводим формулы «=B6*$B$3+C6*$C$3+D6*$D$3», «=B7*$B$3+C7*$C$3+D7*$D$3»,«=B8*$B$3+C8*$C$3+D8*$D$3» соответственно. После открытия окна «Поиск решения» в поле «Оптимизировать целевую функцию» ставим курсор и делаем ссылку на ячейку «F4». В окне появится $F$4. В связи с тем, что целевая функция максимизируется, далее нужно проверить, что флажок ниже поля стоит напротив надписи «Максимум». После ставим курсор в поле «Изменяя ячейки переменных» и обводим ячейки с переменными В3, С3 и D3, выделяя ячейки с переменными. В поле появиться $B$3:$D$3. В нижней части окна находится поле «Ограничения». Добавляем все необходимые ограничения, «F6» « Вводим дополнительное ограничение
рис.2.12. Параметры поиска решения Далее выбираем метод решения «Поиск решения линейных задач симплекс-методом». Для запуска вычислений нажимаем кнопку «Найти решение». Появляется надпись, что решение найдено. Выбираем «Сохранить найденное решение» и «ОК» видим результат.
рис.2.13. Окончательный результат решения по методу свертывания критериев Существующие методы предназначены в основном для сравнения заданных альтернатив и выбора лучшей из них. Довольно часто критерии, по которым оцениваются альтернативы, противоречивы, для них используются разные методы и шкалы оценок. С математической точки зрения не существует идеального способа или метода решения многокритериальных задач оптимизации. Тем не менее, эти методы помогают подготовить всю необходимую для принятия решения информацию таким образом, чтобы помочь лицам принимающее решение максимально точно разобраться в ситуации и принять наиболее обоснованное решение. Пакет MATLAB Современная компьютерная математика предлагает целый набор интегрированных программных систем и пакетов программ для автоматизации математических расчетов: MATLAB, Eureka, Gauss, TK Solver!, Derive, Mathcad, Mathematica, Maple V и др. Среди них, MATLAB занимает одно из лидирующих мест. MATLAB — одна из старейших, тщательно проработанных и проверенных временем систем автоматизации математических расчетов, построенная на расширенном представлении и применении матричных операций. Это нашло отражение в названии системы — MATrix LABoratory — матричная лаборатория [14]. MATLAB является важным инструментом для решения широкого спектра научных и прикладных задач, в таких областях как: моделирование объектов и разработка систем управления, проектирование коммуникационных систем, обработка сигналов и изображений, измерение сигналов и тестирование, финансовое моделирование, вычислительная биология и для многокритериальной оптимизации в том числе [10,23]. В настоящее время MATLAB далеко вышла за пределы специализированной матричной системы и стала одной из наиболее мощных универсальных интегрированных инструментов. Слово «интегрированная» указывает на то, что в этой системе объединены удобная оболочка, редактор выражений и текстовых комментариев, вычислитель и графический программный процессор. В новой версии используются такие мощные типы данных, как многомерные массивы, массивы ячеек, массивы структур, массивы Java и разреженные матрицы, что открывает возможности применения системы при создании и отладке новых алгоритмов матричных и основанных на них параллельных вычислений и крупных баз данных [24,31,35]. В целом MATLAB — это уникальная коллекция реализаций современных численных методов компьютерной математики, созданных за последние три десятка лет. Она вобрала в себя и опыт, правила и методы математических вычислений, накопленные за тысячи лет развития математики. Это сочетается с мощными средствами графической визуализации и даже анимационной графики. Систему с прилагаемой к ней обширной документацией вполне можно рассматривать как фундаментальный многотомный электронный справочник по математическому обеспечению ЭВМ — от массовых персональных компьютеров до супер-ЭВМ [38,54]. MATLAB представляет собой основу всего семейства продуктов MathWorks и является главным инструментом для решения широкого спектра научных и прикладных задач, в таких областях как: 1) Математические расчеты; 2) Разработка алгоритмов; 3) Моделирование; 4) Анализ данных и визуализация; 5) Научная и инженерная графика; 6) Разработка приложений, включая графический интерфейс пользователя. MATLAB развивался в течение нескольких лет, ориентируясь на различных пользователей. В университетской среде, он представлял собой стандартный инструмент для работы в различных областях математики, машиностроении и науки. В промышленности, MATLAB – это инструмент для высокопродуктивных исследований, разработок и анализа данных [55]. В MATLAB важная роль отводится специализированным группам программ, называемых Toolboxes. Они очень важны для большинства пользователей MATLAB, так как позволяют изучать и применять специализированные методы. Это своего рода пакет расширения, позволяющее быстро ориентировать систему на решение задач в той или иной предметной области: в специальных разделах математики, в физике и в астрономии, в области нейронных сетей и средств телекоммуникаций, а так же в математическом моделировании [38,54,55]. Этот пакет подходит для анализа многокритериальных экономических задач линейного программирования. Тщательно рассмотрим систему MATLAB и ее пакеты расширения. Основные компоненты MATLAB |

 . После этого, для остальных критериев вводится система контрольных показателей. Т.е. для каждого критерия нужно задать, что он не должен превышать или быть меньшим, чем некоторое заданное величина. После этого решается задача однокритериальной условной оптимизации, где
. После этого, для остальных критериев вводится система контрольных показателей. Т.е. для каждого критерия нужно задать, что он не должен превышать или быть меньшим, чем некоторое заданное величина. После этого решается задача однокритериальной условной оптимизации, где  стремится к максимуму или минимуму, при условиях, что каждый частный критерий, кроме главного критерия будет больше или равен чем заданное контрольное значения,
стремится к максимуму или минимуму, при условиях, что каждый частный критерий, кроме главного критерия будет больше или равен чем заданное контрольное значения, (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) будут лежать в интервале [0;1].
будут лежать в интервале [0;1]. . Критерии оптимальности - минимум затрат на рекламу, максимум доли рынка и объема продаж в течении заданного периода времени.
. Критерии оптимальности - минимум затрат на рекламу, максимум доли рынка и объема продаж в течении заданного периода времени.  - реклама,
- реклама,  - доля рынка,
- доля рынка,  - объем продаж.
- объем продаж.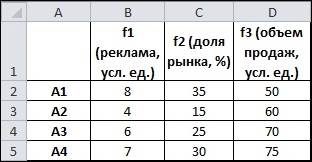


 .
.
 и
и 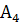 . А для критерия
. А для критерия  и
и  . Новым ограничением, для критерия
. Новым ограничением, для критерия 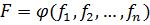 (2.8)
(2.8) от частных критериев
от частных критериев  . В общем случае, функцию
. В общем случае, функцию 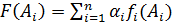 (2.9)
(2.9) выбираются такими, чтобы их сумма была равна единицы
выбираются такими, чтобы их сумма была равна единицы 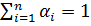 . В методе равномерной оптимизации, который является частным случаем аддитивной свертке, весовые коэффициенты берутся равными друг другу
. В методе равномерной оптимизации, который является частным случаем аддитивной свертке, весовые коэффициенты берутся равными друг другу  . Иногда оказывается более удобным другой подход к определению весовых коэффициентов
. Иногда оказывается более удобным другой подход к определению весовых коэффициентов 
 , произведение частных критериев
, произведение частных критериев  , каждый из которых возведен в степень
, каждый из которых возведен в степень 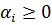 .
. (2.10)
(2.10)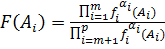 (2.11)
(2.11)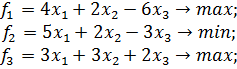


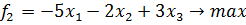 .
. 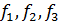 в один, и можем дальше решить задачу обычным путем
в один, и можем дальше решить задачу обычным путем  .
.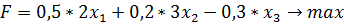 или
или 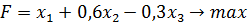 .
. . Для этого в ячейку А3 вводим подпись «Переменные», а соседние три ячейки В2, С2 и D2 вводим значения переменных. Это могут быть произвольные числа, например единицы или нули, далее они будут оптимизироваться. В нашем случае это единицы.
. Для этого в ячейку А3 вводим подпись «Переменные», а соседние три ячейки В2, С2 и D2 вводим значения переменных. Это могут быть произвольные числа, например единицы или нули, далее они будут оптимизироваться. В нашем случае это единицы.
 » «F6», «F7:F8» «≤» и «G7:G8».
» «F6», «F7:F8» «≤» и «G7:G8».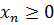 , и получим следующую формулу «B3:D3», «
, и получим следующую формулу «B3:D3», «