
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тестирование программного обеспеченияСодержание книги
Поиск на нашем сайте
По окончании разработки программное обеспечение подверглось тщательному тестированию. Тестирование выполнялось в локальной сети ЗАО МЗХ «Атлант». На сервере была размещена база данных штрих-кодов изделий предприятия, сформированная ранее. Процедура тестирования заключалась в следующем: а) Выполнение стандартных действий при считывании штрих-кодов. С помощью программы выполнялись операции считывания штрих-кодов с этикеток, проверка по базе данных и добавление данных в таблицу. При этом не было замечено никаких отклонений от нормального хода выполнения программы, т.е. все ее действия были предсказуемы. Тестирование выполнялось на довольно значительном массиве данных. При этом каких-то значительных задержек при обработке и сохранению в базу данных не было. При считывании информации и добавлении в окно главной формы программы происходили небольшие задержки времени. Это объясняется тем, что для избегания перегрузки процессора бесконечным циклом была специально установлена задержка в 50 миллисекунд и временной задержкой сканера между двумя считываниями. б) Создание нестандартных ситуаций, требующих особой обработки. При тестировании программного обеспечения создавались ситуации типа считывания штрих-кода длинной более двенадцати символов. Программа корректно обрабатывала данные, как, и было задумано. Другой исключительной ситуацией было открытие последовательного порта, когда он был занят уже другим приложением. Это событие обрабатывалось программой аналогичным образом. При попытке открытии таблицы, занятой другим приложением, было выдано сообщение о данной проблеме. В ходе испытаний была доказана полная совместимость и правильность работы программного средства с OC Windows XP. Произведём оценку надежности ПО. Все модели надежности ПО можно разделить на два класса: иерархические и математические. Иерархические модели надежности ПО позволяют выполнить интегральную количественную оценку надежности ПС, учитывающую различные критерии надежности[13]. Математические модели надёжности ПО позволяют определить оценки показателей надёжности ПО: вероятность безотказной работы
Произведём оценку надежности данного программного обеспечения с помощью математической модели Джелинского-Моранды. Допущения модели[13]: а) время до очередного отказа распределено по экспоненциальному закону; б) все ошибки равновероятны и их появление не зависит друг от руга; в) частота появления ошибок (интенсивность отказов, в англоязычной литературе так же имеет название функция риска) пропорциональна числу не выявленных ошибок:
где:
г) д) каждая обнаруженная ошибка в ПО немедленно устраняется и число оставшихся ошибок уменьшается на 1; е) ошибки корректируются без внесения новых ошибок. Характеристиками модели (то, что нужно определить) являются: – – – – Характеристики модели определяются при помощи метода максимального правдоподобия. При тестировании фиксировались интервалы времени между отказами вследствие ошибок в ПО { Введём понятие о функции правдоподобия L как о совместной n-мерной плотности распределения вероятностей события, заключающегося в том, что в процессе тестирования ПО случайная величина T примет значение t1=10 часов, t2=15 часов, t3=20 часов, t4=25 часов. Функция правдоподобия согласно допущению модели Джелинского – Моранди, что все ошибки равновероятны и их появления не зависят друг от друга, будет иметь вид (4.2):
или, подставив значения функции плотности,
В качестве оценок неизвестных параметров
и выбирается то решение, которое обращает функцию правдоподобия в максимум. Так как экстремум функций L и lnL достигается при одних и тех же значениях Возьмём натуральный логарифм от функции правдоподобия, чтобы произведение функций заменить суммой:
Возьмём частные производные по
Полагая а) оценка коэффициента Джелинского – Моранды
б) оценка числа ошибок в ПО до начала тестирования
Интенсивность отказов до следующей пятой ошибки
Средняя наработка до обнаружения следующей пятой ошибки
Вероятность безотказной работы, т.е. отсутствия следующего пятого отказа
Оценка надежности программного обеспечения с помощью модели Джелинского-Моранды показала, что разработанное ПО автоматизированной системы идентификации готовой продукции соответствует предъявляемым требованиям надежности. Средняя наработка до обнаружения пятой ошибки составила 58,82 часа.
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.148.63 (0.009 с.) |

 , интенсивность отказов
, интенсивность отказов 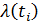 , математическое ожидание времени наработки на отказ
, математическое ожидание времени наработки на отказ  , число ошибок в ПО до начала тестирования
, число ошибок в ПО до начала тестирования  [13].
[13].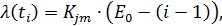 (4.1)
(4.1) – коэффициент Джелинского-Моранды;
– коэффициент Джелинского-Моранды;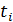 – интервал времени между
– интервал времени между  -й и -й обнаруженными ошибками;
-й и -й обнаруженными ошибками;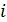 – число ошибок, обнаруженных к моменту отладки
– число ошибок, обнаруженных к моменту отладки  на интервале между двумя смежными моментами появления ошибок;
на интервале между двумя смежными моментами появления ошибок;


 , которые максимизируют функцию правдоподобия. Затем, на основании известных правил дифференциального исчисления для нахождения оценок максимального правдоподобия
, которые максимизируют функцию правдоподобия. Затем, на основании известных правил дифференциального исчисления для нахождения оценок максимального правдоподобия  и
и  составляется система уравнений (4.4)
составляется система уравнений (4.4)


 и
и  и решая систему уравнений, получаем:
и решая систему уравнений, получаем:







