
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дать определение потенциального силового поля. Доказать свойства стационарного потенциального силового поля.Содержание книги
Поиск на нашем сайте
Силовое поле - часть пространства, в кот. на движущуюся материальную точку действуют силы, зависящие от корд. точки и t, но не зависящие от скорости. Если сила явно не зависит от t, то силовое поле - стационарное. Ф-ция Ф-ция - Элемент. работа силы стационарного пот. поля равна полному дифф. силовой ф-ции. - Полная работа силы стационарного пот. поля не зависит от формы траектории, по которой перемещается точка, и опред. нач. и конеч. положениями точки. - Из (2): что работа силы - Чтобы стационарное силовое поле было пот. оно должно быть безвихревым:
Докажем: для производных высших порядков, порядок дифф. значения не имеет: Дать определение поверхности уровня потенциального силового поля и доказать их свойства. Пов. уровня (эквипотенциальная пов.) - геометрическое место точек пот. силового поля, для которых значения силовой ф-ции постоянно. Ур-е пов.: - Нач. и конеч. точка перемещ. лежат на одной пов. уровня, то работа стационарного пот. поля по перемещ. точки равна нулю. - Сила - Сила в пот. силовом поле напр. в сторону возрастающих значений силовой ф-ции. Точка М перемещ. с пов. уровня - Если силовое поле разбить пов. уровня, то там, где соседние пов. уровня ближе друг к другу, величина силы больше, чем в местах, где пов. уровня дальше друг от друга, так как работа между точками соседних пов. в этом случае одна и та же. Силовая линия - кривая, касат. к которой в каждой точке совпадает с направл. силы поля в этой точке. Вектор
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.76.183 (0.005 с.) |

 зависит только от координат, частные производные от этой ф-ции по координатам равны проекциям силы силового поля на соотв. оси:
зависит только от координат, частные производные от этой ф-ции по координатам равны проекциям силы силового поля на соотв. оси:  ;
; 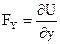 ;
;  (1)
(1) .
.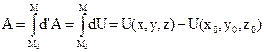 (2)
(2) стационарного пот. поля по любому замкнутому перемещ. равна нулю. Силовая ф-ция может принимать другие значения после возвращения в начальную точку в зависимости от числа обходов, если внутри замкнутого конура есть особые точки.
стационарного пот. поля по любому замкнутому перемещ. равна нулю. Силовая ф-ция может принимать другие значения после возвращения в начальную точку в зависимости от числа обходов, если внутри замкнутого конура есть особые точки. ;
;  ;
; 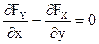 или кратко: rot
или кратко: rot 
 , аналогично и остальные.
, аналогично и остальные. .
.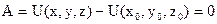 .
.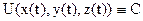 . Продифф. по t:
. Продифф. по t:  . Учитывая:
. Учитывая: 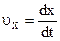 ;
;  ;
;  , имеем:
, имеем:  или
или  - условие перпендикулярности векторов
- условие перпендикулярности векторов  .
. на другую пов. уровня
на другую пов. уровня  . Работа силы
. Работа силы  направлен по касат., из условия паралл.
направлен по касат., из условия паралл.  - ДУ силовой линии стационар. поля. Для пот. поля:
- ДУ силовой линии стационар. поля. Для пот. поля:  .
.


