
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте математическую постановку и изложите решение двух основных задач динамики точки.Стр 1 из 3Следующая ⇒
Сформулируйте математическую постановку и изложите решение двух основных задач динамики точки. Первая: Зная закон движения материальной точки массы m, найти равнодействующую всех сил Движение точки задано координатным способом, т.е. Вторая: По заданной силе
Решение сводиться к интегрированию системы трех ДУ второго порядка. Общее решение этой системы будет содержать 6 произвольных постоянных:
Константы найдём из начальных условий: Вывести закон движения материальной точки, брошенной под углом к горизонту. Материальная точка М массой m, брошена с поверхности под углом Единственной силой, является сила тяжести: Проинтегрируем ДУ движения точки: Интегрируем еще раз: Для определения постоянных Поставим начальные условия в (2) и в (3): Подставим постоянные в (3): Доказать необходимое и достаточное условия прямолинейного движения материальной точки и записать дифференциальное уравнение её прямолинейного движения. ДУ свободной материальной точки в проекциях на декартовы оси координат:
Точка движется по прямой (ось Ох). Уравнения прямолинейной траектории точки: y = 0, z = 0 (2), следовательно, на основании (1):
Вывести дифференциальное уравнение вынужденных колебаний механической системы с одной степенью свободы без учета сопротивления. Изложить его решение в случае резонанса. Графики амплитуды и сдвига фаз вынужденных колебаний. Q(t) - обобщенная сила характеризующая внешнее воздействие на колебательную систему.
Определяем положение системы обобщенной координатой q, при равновесии Уравнение Лагранжа II рода: Так как равновесие устойчиво, а возмущения малы, для Т и П воспользуемся выражениями: Поставляя (2) в (1), получим:
Решение q(t) это сумма общего решения Однородное уравнение для определения Частное решение k=p
Далее, учитывая общее решение уравнения и частное, запишем общее решение для (1):
Постоянные
.
59.Дать определение явления удара. Изложить основные понятия и допущения элементарной теории удара. Явление, при котором за малый промежуток времени скорость точек тела изменяется на конечную величину, называется ударом. Малый промежуток времени
Силы, возникающие при ударе и действующие в течение времени удара, но достигающие таких больших значений, что их импульсы за это время становятся конечными величинами, называются ударными силами. Измерять столь большие силы трудно, удобнее измерять ударную силу ее импульсом:
1-ый интеграл - ударный импульс 2-ой интеграл - импульс конечно силы Из (2) следует, что импульсом конечных сил можно пренебречь, его величина того же порядка, что и Т.к. время удара
Сформулируйте математическую постановку и изложите решение двух основных задач динамики точки. Первая: Зная закон движения материальной точки массы m, найти равнодействующую всех сил Движение точки задано координатным способом, т.е. Вторая: По заданной силе
Решение сводиться к интегрированию системы трех ДУ второго порядка. Общее решение этой системы будет содержать 6 произвольных постоянных:
Константы найдём из начальных условий:
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.18.87 (0.017 с.) |
 , действующих на точку в каждый данный момент.
, действующих на точку в каждый данный момент.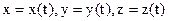 (1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат:
(1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат:  . Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы
. Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы 
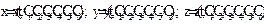
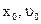 при
при  .
. к горизонту с начальной скоростью
к горизонту с начальной скоростью 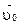 . Начальные условия (t = 0):
. Начальные условия (t = 0): 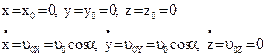 (1).
(1).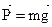 , направленная вниз. Проекции этой силы на оси координат:
, направленная вниз. Проекции этой силы на оси координат:  . ДУ движения точки:
. ДУ движения точки: 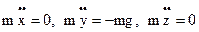 .
.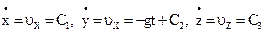 (2)
(2)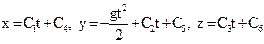 (3).
(3). воспользуемся начальными условиями.
воспользуемся начальными условиями.
 - закон движения точки.
- закон движения точки. (3). Равенства (3) означают, что если точка движется прямолинейно, то равнодействующая сил имеет постоянное направление и совпадающее с прямой, вдоль которой движется точка, то есть в осью Ох. Необходимое условие (3) не является достаточным. При условиях (3) уравнения (1) примут вид:
(3). Равенства (3) означают, что если точка движется прямолинейно, то равнодействующая сил имеет постоянное направление и совпадающее с прямой, вдоль которой движется точка, то есть в осью Ох. Необходимое условие (3) не является достаточным. При условиях (3) уравнения (1) примут вид:  . Интегрируем:
. Интегрируем:  . Ещё раз:
. Ещё раз: 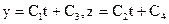 (4). Для опр. постоянных, восп. нач. усл. (t = 0):
(4). Для опр. постоянных, восп. нач. усл. (t = 0): 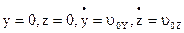 . Постоянные:
. Постоянные:  . Подставим постоянные в (4):
. Подставим постоянные в (4): 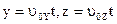 (5). Из (5) видно, что траектория движения точки будет прямой, когда:
(5). Из (5) видно, что траектория движения точки будет прямой, когда: 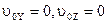 (6). Из равенств (3) и (6) следует, что свободная точка движется по прямой траектории, когда сила, приложенная к точке, имеет постоянное направление и начальная скорость точки параллельная этому направлению.
(6). Из равенств (3) и (6) следует, что свободная точка движется по прямой траектории, когда сила, приложенная к точке, имеет постоянное направление и начальная скорость точки параллельная этому направлению.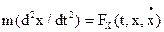 - ДУ прямолинейного движения свободной материальной точки.
- ДУ прямолинейного движения свободной материальной точки. , где: H - амплитуда, p - циклическая (круговая) частота,
, где: H - амплитуда, p - циклическая (круговая) частота,  - начальная фаза обобщенной силы.
- начальная фаза обобщенной силы.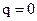 .
.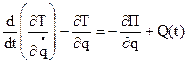 (1).
(1). ,
, 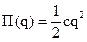 . Находим:
. Находим:  (2).
(2).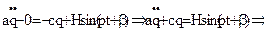
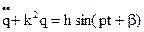 , где:
, где:  = const, круговая или циклическая частота собственных колебаний системы,
= const, круговая или циклическая частота собственных колебаний системы,  = const.
= const.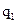 однородного уравнения и частного решения
однородного уравнения и частного решения  неоднородного уравнения, то есть:
неоднородного уравнения, то есть: 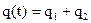 .
. .
. ) и резонанс (
) и резонанс ( ).
).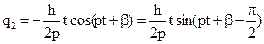 - частное решение (1)
- частное решение (1) , или в амплитудной форме:
, или в амплитудной форме: .
.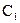 и
и  определяются из начальных условий:
определяются из начальных условий: 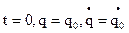 .
.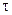 , в течение которого длиться удар, называется временем удара.
, в течение которого длиться удар, называется временем удара.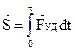 , который называется ударным импульсом, или просто ударом.
, который называется ударным импульсом, или просто ударом. Точка М массой m движется под действием силы
Точка М массой m движется под действием силы  , описывая траекторию
, описывая траекторию  . В точке М в момент t, когда точка имела скорость
. В точке М в момент t, когда точка имела скорость  , произошел удар. Под действием ударной силы
, произошел удар. Под действием ударной силы  точка изменила модуль и направление скорости. Скорость точки после удара
точка изменила модуль и направление скорости. Скорость точки после удара  . Теорема об изменении кол-ва движения точки за время удара:
. Теорема об изменении кол-ва движения точки за время удара:  (1).
(1). (конечная величина).
(конечная величина). (2).
(2). (3): изменение количества движения материальной точки за время удара равно ударному импульсу, приложенному к точке. (3) - основное уравнение динамики точки при ударе.
(3): изменение количества движения материальной точки за время удара равно ударному импульсу, приложенному к точке. (3) - основное уравнение динамики точки при ударе.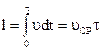 ,
, 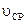 - конечная величина,
- конечная величина, 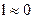 .
.


