
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сечения эллипсоида плоскостями, параллельными плоскостям симметрии. ⇐ ПредыдущаяСтр 3 из 3
a) Сечение ● если
● если ● если b) Сечение ● если
● если ● если c) Сечение ● если
● если ● если
Уравнение однополостного гиперболоида
Свойство симметрии однополостного гиперболоида Утверждение. У однополостного гиперболоида координатные плоскости являются плоскостями симметрии, оси координат являются осями симметрии, начало координат – центром симметрии. Доказательство аналогично доказательству свойств симметрии эллипсоида.
Сечения однополостного гиперболоида плоскостями, параллельными плоскостям симметрии. 1. В сечении
где действительная полуось равна b, а мнимая полуось равна с. 2.
3. Сечения плоскостей В сечении
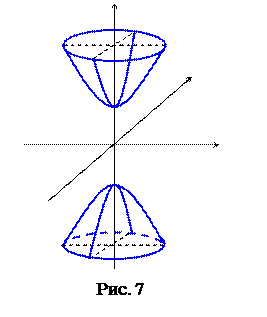
Уравнение двуполостного гиперболоида
Свойство симметрии двуполостного гиперболоида У двуполостного гиперболоида координатные плоскости являются плоскостями симметрии, оси координат являются осями симметрии, начало координат – центром симметрии.
Сечения двуполостного гиперболоида плоскостями, параллельными плоскостям симметрии. 1) В сечении ●
● ● 2) При
3) При 4) Сечения плоскостей
Уравнение эллиптического параболоида
Свойство симметрии эллиптического параболоида В отличии от эллипсоида и гиперболоидов, плоскость xOy не является плоскостью симметрии, следовательно оси Ox и Oy не являются осями симметрии. Если · · · У эллиптического параболоида нет центра симметрии.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.24.134 (0.012 с.) |
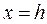 (плоскость
(плоскость 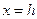 параллельна плоскости yOz).
параллельна плоскости yOz). получается эллипс:
получается эллипс: , где
, где 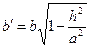 ;
; 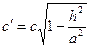
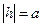 , то
, то 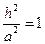 ,
, 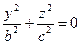 ,
, 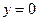 и
и 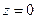 – точки с координатами:
– точки с координатами:  ,
,  – вершины эллипсоида.
– вершины эллипсоида.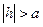 – точек пересечения нет.
– точек пересечения нет. (плоскость
(плоскость 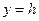 параллельна плоскости xOz)
параллельна плоскости xOz)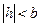 получается эллипс:
получается эллипс: , где
, где  ;
; 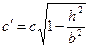
 , то
, то  ,
, 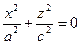 ,
, 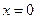 и
и 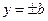 ,
, 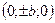 – вершины эллипсоида.
– вершины эллипсоида.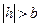 – точек пересечения нет.
– точек пересечения нет.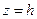 (параллельных плоскости xOy)
(параллельных плоскости xOy)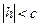 получается эллипс:
получается эллипс:
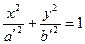 , где
, где  ;
; 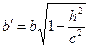 .
.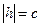 , то
, то  ,
, 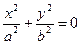 ,
, 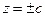 , то есть
, то есть 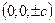 – вершины эллипсоида.
– вершины эллипсоида. – точек пересечения нет.
– точек пересечения нет.

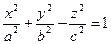 .
.
 ,
, В сечении
В сечении 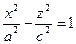
 и
и 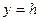 аналогичны сечениям плоскостей
аналогичны сечениям плоскостей 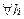 . А при
. А при 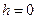 получается эллипс - горловина однополостного гиперболоида:
получается эллипс - горловина однополостного гиперболоида: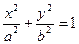 .
.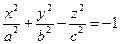 .
.
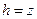 :
:
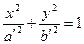 , где
, где  ,
, 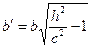 .
. .
.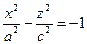 .
.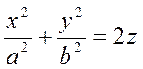 .
.
 параболоиду, то
параболоиду, то параболоиду
параболоиду  yOz – плоскость симметрии параболоида;
yOz – плоскость симметрии параболоида;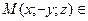 параболоиду
параболоиду  параболоиду
параболоиду 


