
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вектори. Лінійні операції над векторамиСтр 1 из 2Следующая ⇒
Приклади для самостійного розв’язання
Відповіді. 2.
Розклад даного вектора за напрямками на прямій, на площині і в просторі Означення. Вектор У виразі (1) вектор В необхідності розкладу вектора за даними напрямками можна переконатись на такому прикладі. Дві опори (рис. 9) утримують вантаж під дією сили земного тяжіння
Рис. 9 Для розв’язання задачі розкладемо вектор Пропонуємо самостійно переконатись, що
Тепер перейдемо до лінійного вираження вектора за напрямками в більш загальній формі: на прямій, на площині в просторі. 1. Нехай дано два ненульові колініарні вектори
Дійсно, 2. Нехай на площині задані два неколініарні вектори
Рис. 10
Але Отже,
Коефіцієнти розкладу 3. Нехай в просторі задано три некомпланарні вектори
де
Рис. 11
Для доведення (3) проведемо з точки А (кінець вектора
Вектор
Крім того, P(0,3,5), Q(9,-3,-1). 2.7. Кут між векторами. Проекція вектора на вісь. Властивості проекцій
1. Кут між векторами. Нехай задані ненульові вектори Менший з кутів, які утворені цими променями називається кутом між векторами Кут між вектором Очевидно, що якщо Вправи. 1). Знайти 2). Нехай
Рис. 15
3). Розглянемо рівнобедренний прямокутний трикутник АВС, де
Відповіді: 2. Проєкцію вектора Очевидно, що коли Основні властивості проекцій: 1. 2. 3. Властивість 3 виконується для суми скінченного числа векторів.
Скалярний добуток векторів
Означення. Скалярним добутком
На основі властивості 1 проекцїї вектора рівність (1) запишеться:
У фізиці робота А сталої сили
Основні властивості скалярного добутку.
Випливає із (1).
Таблиця скалярного множення ортів. Згідно означення (1) Отже, скалярний добуток одноіменних ортів дорівнює одиниці, а різноіменних - 0. Скалярний добуток векторів в координатній формі. Якщо Дійсно, за допомогою властивостей
Оскільки добуток одноіменних ортів дорівнює 1, а різноіменних – 0, то отримуємо формулу скалярного добутку у координатній формі:
Приклад 1. Знайти скалярний добуток векторів Розв’язання: За формулою (3) маємо:
Приклад 2. Задані точки А(3,2,3), В(1,-4,3), С(-4,5,1). Знайти скалярний добуток векторів Розв’язання. Спочатку знайдемо вектори
За формулою (3) маємо
Довжина вектора. Якщо в (1)
Відстань між двома точками.
Косинус кута між двома векторами отримаємо із формули (1) із врахуванням (3) і (4):
Приклад 3. Задані точки Розв’язання. Знаходимо вектори
Приклад 4. Знайти модуль вектора
Розв’язання. За формулою (4)
тоді
Умова перпендикулярності двох ненульових векторів
Проекція вектора на вектор знаходиться із врахуванням (3) і (4):
Теорема. Декартові прямокутні координати Дійсно, згідно з (9) маємо
Напрямними косинусами вектора
Приклад. Знайти напрямні косинуси вектора Розв’язання.
Рис. 19 Легко перевірити, що для довільного вектора
Напрямні косинуси вектора
Таблиця векторного множення ортів.
Векторний добуток одноіменних ортів дорівнює Формули векторного добутку в координатній формі отримуємо із врахуванням таблиці векторного добутку ортів
Приклад 1. Знайти векторний добуток векторів Розв’язання. Зауважимо, що визначник (1) зручніше обчислювати, застосувавши теорему про розклад (див. І, 1.4) за елементами першого рядка:
Тепер побудуємо вектори
З рисунка видно, що положення знайденого вектора Приклад 2. Знайти площу трикутника АВС, якщо А(1,-2,-1), В(2,3,1), С(0,1,4). Розв’язання. Знаходимо вектори
Довжина отриманого вектора за означенням чисельно дорівнює площі паралелограма, побудованого на даних векторах. Тому
а площа
Вектори. Лінійні операції над векторами 1. Скалярні і векторні величини. Величина, для характеристики якої досить її числового значення у відповідних одиницях вимірювання, називається скалярною. Прикладами скалярних величин є маса, температура, довжина, площа, об’єм, кількість тепла і т.п.
Величина, для характеристики якої крім числового значення вказується ще і напрямок в просторі, називається векторною. Наприклад: сила, швидкість, прискорення, напруженість поля (електростатичного, магнітного, електромагнітного) і т.п. Геометричним зображенням векторної величини в заданому масштабі є вектор. Вектором називається відрізок заданої довжини і вказаним напрямком в просторі, тобто направлений відрізок.
А Рис. 1
На рис. 1 А - початкова точка вектора, В - кінець вектора, вектор позначають Якщо початок і кінець вектора збігаються, то такий вектор називається нульовим і позначають Два ненульові вектори, що лежать на паралельних прямих або на одній прямій називають колінеарними, позначається Вектори паралельні одній і тій же площині, або ті що лежать в одній площині називаються компланарними. Рівними називаються два вектори, якщо вони задовольняють умови: 1) вони колінеарні, 2) їх модулі рівні, 3) вони направлені в одну сторону, тобто
Наприклад, на рис. 2, де АВСD - паралелограм,
Рис. 2 вектори Якщо З означення рівності векторів випливає, що вектор можна переносити в просторі паралельно самому собі, такі вектори називають вільними. Вектор, модуль якого дорівнює одиниці називається одиничним вектором, або ортом, і позначається
2. Лінійні операції над векторами. До них відносяться додавання векторів та множення вектора на число (скаляр). Додавання векторів. Нехай задані два вектори
Рис. 3 Сумою двох векторів Згідно рис. 3 вектор
За принципом замикання знаходиться сума більшого числа доданків.
Рис. 4
Різниця векторів. Помістимо початки векторів
Рис.5
Різницею двох векторів Множення вектора на число. Добутком ненульового вектора Напрямок вектора
При
Рис. 6
3. Властивості лінійних операцій над векторами.
Властивість 1, що називається переставною або комутативною, зрозуміла з рис. 7, дозволяє додавати вектори за правилом паралелограма.
Рис. 8
Властивості 3 - 8 пропонуємо перевірити самостійно. Приклад 1. За даними векторами а ) Розв’язання. Див. на рис. а) і б)
Приклад 2. У трикутнику АВС проведена медіана АМ див. на рис. Виразити вектор
Розв’язання. За означенням різниці векторів За означенням суми векторів із ∆ АВМ маємо
|
||||||||
|
Последнее изменение этой страницы: 2017-02-16; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.136.170 (0.141 с.) |
 і
і  побудувати такі вектори: 1)
побудувати такі вектори: 1) 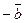 ; 2)
; 2) 
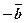 ; 3)
; 3) 

 ,
,  . Виразити через
. Виразити через  вектори
вектори 

 .
. через вектори
через вектори  .
. , якщо
, якщо 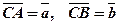 .
.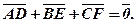

 3.
3.  ;
;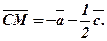 4.
4. 
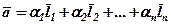 (1) називається лінійною комбінацією
(1) називається лінійною комбінацією  векторів
векторів  , де
, де  -деякі числові множники.
-деякі числові множники. отримано в результаті лінійних операцій над векторами
отримано в результаті лінійних операцій над векторами 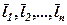 . Іноді говорять, що вектор
. Іноді говорять, що вектор  . Необхідно знайти зусилля на кожну з опор.
. Необхідно знайти зусилля на кожну з опор.
 і
і  ,
,  можна знайти за допомого теореми синусів, розглядаючи паралелограм АВСО, в якому відома діагональ
можна знайти за допомого теореми синусів, розглядаючи паралелограм АВСО, в якому відома діагональ  і кути
і кути 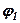 і
і  , які вона утворює зі сторонами ОВ і ОС.
, які вона утворює зі сторонами ОВ і ОС.
 ,
,  . Тоді існує число
. Тоді існує число  таке, що
таке, що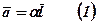
 можна знайти як відношення
можна знайти як відношення  . Якщо вектори
. Якщо вектори  однаково напрямлені,
однаково напрямлені,  , то число
, то число  , то
, то  ,
,  ½½
½½  , і вектор
, і вектор  (рис. 10).
(рис. 10).
 , а сторони ОВ і ОС розміщені на напрямках векторів
, а сторони ОВ і ОС розміщені на напрямках векторів 
 , тоді за аналогією з (1) існує число
, тоді за аналогією з (1) існує число  . Так само
. Так само 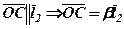 .
.
 називаються координатами вектора
називаються координатами вектора  зведені до спільної точки О і вектор
зведені до спільної точки О і вектор 
 - деякі числа, називаються координатами вектора
- деякі числа, називаються координатами вектора  (рис. 11).
(рис. 11).
 до перетину з площиною векторів
до перетину з площиною векторів 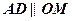 до перетину з напрямком
до перетину з напрямком 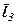 в точці
в точці  . ОМАD - паралелограм. Для вектора
. ОМАD - паралелограм. Для вектора  .
. компланарний з
компланарний з 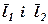 , тому згідно (2) існують числа
, тому згідно (2) існують числа 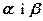 такі, що
такі, що
 , тому за аналогією з (1) існує число
, тому за аналогією з (1) існує число  таке, що
таке, що  . Остаточно отримуємо рівність (3).
. Остаточно отримуємо рівність (3). . Зведемо ці вектори до спільної точки О і в напрямках векторів
. Зведемо ці вектори до спільної точки О і в напрямках векторів  проведемо з точки О промені (див. рис. 15).
проведемо з точки О промені (див. рис. 15). .
. , то
, то  ; Якщо ж
; Якщо ж  то
то  .
. ,
,  ,
,  .
.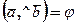 . Знайти
. Знайти 
 .
.
 . Знайти
. Знайти 
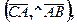



 (позначається
(позначається  ) називається довжина відрізка, який сполучає проекції на цю вісь початку і кінця вектора, взята зі знаком «+», якщо кут між вектором і віссю гострий і знаком «-», якщо цей кут тупий (рис. 16).
) називається довжина відрізка, який сполучає проекції на цю вісь початку і кінця вектора, взята зі знаком «+», якщо кут між вектором і віссю гострий і знаком «-», якщо цей кут тупий (рис. 16). , то
, то  (рис. 16);
(рис. 16); =
=  (рис. 17);
(рис. 17);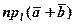 =
=  (рис. 18).
(рис. 18).
 двох векторів
двох векторів 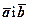 (позначається
(позначається  ) називається число рівне добуткові модулів цих векторів, помноженому на косинус кута між ними:
) називається число рівне добуткові модулів цих векторів, помноженому на косинус кута між ними: . (1)
. (1) (2)
(2) при прямолінійному переміщенні вздовж вектора шляху
при прямолінійному переміщенні вздовж вектора шляху 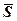 знаходиться як скалярний добуток цих векторів:
знаходиться як скалярний добуток цих векторів: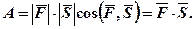
 Скалярний добуток комутативний
Скалярний добуток комутативний .
. Числовий множник
Числовий множник  можна виносити за знак скалярного добутку:
можна виносити за знак скалярного добутку: .
. Для довільних векторів
Для довільних векторів 
 .
.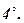 Скалярний добуток двох векторів
Скалярний добуток двох векторів  ) тоді і тільки тоді, коли один із них є нульовим вектором, або коли ці вектори перпендикулярні
) тоді і тільки тоді, коли один із них є нульовим вектором, або коли ці вектори перпендикулярні  .
. , аналогічно
, аналогічно  , а за властивістю (4)
, а за властивістю (4) 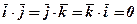 .
. , то
, то 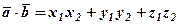 .
. маємо
маємо
 і
і  .
.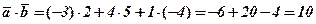 .
. .
.

 .
. , то
, то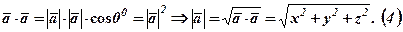
 і
і  знаходиться як довжина вектора
знаходиться як довжина вектора  за формулою (4):
за формулою (4):

 . Для паралелограма, побудованого на векторах
. Для паралелограма, побудованого на векторах  і
і  обчислити: 1)довжини сторін, тобто
обчислити: 1)довжини сторін, тобто  і
і  ; 2) косинус та синус, кута
; 2) косинус та синус, кута  ; 3) площу.
; 3) площу.
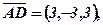 тоді: 1)
тоді: 1) 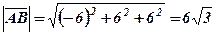 ,
,  . 2)
. 2) 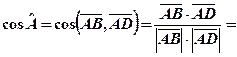
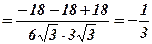 (кут
(кут  - тупий),
- тупий), 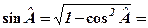
 . 3)
. 3) 
 .
. , якщо
, якщо .
. . Знаходимо
. Знаходимо
 ,
,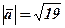 .
.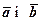 випливає із властивості 4° і формули (3)
випливає із властивості 4° і формули (3)


 вектора
вектора  є його проекціями на відповідні осі координат.
є його проекціями на відповідні осі координат.
 , утворених між вектором
, утворених між вектором 
 та значення виразу
та значення виразу  .
.

 .
.

 повністю визначають напрямок вектора і є координатами одиничного вектора
повністю визначають напрямок вектора і є координатами одиничного вектора  , що збігається за напрямком з
, що збігається за напрямком з 


 . При найкоротшому повороті від одного орта до іншого проти годинникової стрілки отримуємо третій орт, за годинниковою стрілкою - третій орт із знаком «-».
. При найкоротшому повороті від одного орта до іншого проти годинникової стрілки отримуємо третій орт, за годинниковою стрілкою - третій орт із знаком «-».
 =(0,2,1). Побудувати в системі координат вектори
=(0,2,1). Побудувати в системі координат вектори  .
.
 за їх координатами.
за їх координатами.
 відповідає означенню векторного добутку
відповідає означенню векторного добутку  .
. і їх векторний добуток:
і їх векторний добуток:
 .
. АВС складає половину знайденої площі, тобто
АВС складає половину знайденої площі, тобто
 В
В . Для зручності запису замість символа «
. Для зручності запису замість символа « » над вектором будемо писати «—». Іноді вектор позначають однією буквою:
» над вектором будемо писати «—». Іноді вектор позначають однією буквою:  .
. . Напрямок нульового вектора може бути довільним.
. Напрямок нульового вектора може бути довільним. . Нульовий вектор вважається колінеарним довільному вектору.
. Нульовий вектор вважається колінеарним довільному вектору.


 , то вектори
, то вектори  . Вектор
. Вектор  і записують
і записують  .
. :
: .
. . Відкладемо з деякої точки О вектор
. Відкладемо з деякої точки О вектор  , а тоді з точки А відкладемо вектор
, а тоді з точки А відкладемо вектор  і розглянемо вектор
і розглянемо вектор 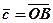 .
.
 , початок якого знаходиться в початку вектора
, початок якого знаходиться в початку вектора 
 .
.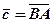 (рис. 5).
(рис. 5).
 ), напрямок якого вибирається в сторону заменшуваного.
), напрямок якого вибирається в сторону заменшуваного. .
.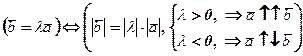

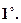

 Рис. 7
Рис. 7
 - асоціативна або сполучна властивість (див. рис. 8).
- асоціативна або сполучна властивість (див. рис. 8).


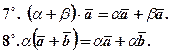
 .
.
 через вектори
через вектори  і
і  .
.
 , тоді
, тоді 




