
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение матричных игр С помощью линейного программирования в среде Excel ⇐ ПредыдущаяСтр 5 из 5
1.Освоить алгоритм перехода от задачи теории игр к задаче линейного программирования; 2. Получить навык решения матричных игр с помощью линейного программирования в среде EXCEL. Решение матричной игры сведением к задаче линейного программирования в среде Excel
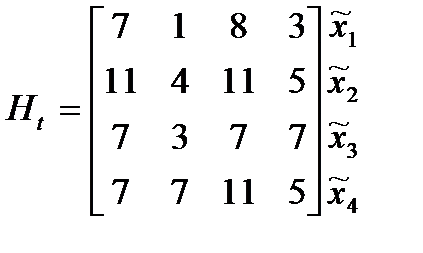
Среди элементов матрицы есть отрицательные
Введем переменные для игрока
ПЗЛП для игрока 1:
ДЗЛП для игрока 2:
Таблица - Решение ПЗЛП в среде Excel
Переход к решению исходной игры.
Проверка: Произведение двух векторов и матрицы, взятое в заданном порядке, равно цене игры:
Ответ:
Обоснование распределения финансовых ресурсов между проектами. На инвестирование трех проектов выделено В млн. руб. Известна эффективность капитальных вложений xi в каждый j -й проект, заданная таблично значением нелинейной функции fj (xi), где Необходимо распределить выделенные средства между проектами таким образом, чтобы получить максимальный суммарный доход.
Исходные данные варианта 0:
Математическая модель задачи. Определить х * = (
и удовлетворяющий условиям
Математическая модель задачи варианта 0:
при ограничениях:
Условная оптимизация. Максимально возможный доход, который может быть получен с проектов (с k -го по n -й), определяется с помощью функции Беллмана:
где Сk – количество средств, инвестируемых в k -е проект, 0≤ Сk ≤ В. На первом шаге условной оптимизации при k = n функция Беллмана представляет собой прибыль только с n -го проекта. При этом на его инвестирование может остаться количество средств Сn, 0 ≤ Сn ≤ В. Чтобы получить максимум прибыли с этого проекта, можно вложить в него все эти средства, т.е. Fn (Сn) = fn (Сn) и хn = Сn. Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах xi = {0, 100, 200, 300, 400, 500, 600, 700} тыс. руб. Решение. I этап. Условная оптимизация. 1-й шаг: k = 3. Таблица 1
В шапке таблицы отражены варианты значений капиталовложений х3, которые могут быть предоставлены третьему проекту. В столбце C3 отражены варианты значений капиталовложений, которые могут быть выделены всем трем проектам в совокупности. Предположим, что все средства в количестве x3 = 700 тыс. руб. отданы третьему проекту. В этом случае максимальный доход составит f 3(x 3) = 700 тыс. руб., следовательно: F 3(C3) = f 3(x 3) и x 3= C3.
2-й шаг: k = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим проектами. При этом рекуррентное соотношение Беллмана имеет вид:
Представим в таблице расчет функции Беллмана. Таблица 2
В шапке таблицы отражены варианты значений капиталовложений х2, которые могут быть предоставлены второму проекту при условии, что часть средств выделяется третьему проекту. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции при втором проекте f2 (х2) в результате освоения капиталовложений х2; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F 3(C2 – х2), т.е. возможный прирост выпуска продукции при третьем проекте, если ему будет выделена оставшаяся часть капиталовложений, определяемая как C2 – х2. Например, рассуждая формально, если при общей величине капиталовложений C2 = 0 второму проекту выделяется х2 = 0, то прирост продукции составляет f2 (0) = 0, а значение функции Беллмана из табл.1 составит: F 3(0 – 0) = 0. Поэтому в клетке табл. 2 (0, 0) отражается сумма 0+0. При общей величине капиталовложений C2 = 100 тыс. руб. возможны уже два варианта распределения средств между вторым и третьим проектами: 1) второму проекту ничего не выделяется, т.е. х2 = 0 и прирост продукции составляет f2 (0) = 0. В этом случае значение функции Беллмана из табл. 1 составит F 3(100 – 0) = F 3(100) = 40 тыс. руб., т.е. вся сумма C2 = 100 тыс. руб. выделена третьему проекту, поэтому суммарный прирост продукции составит 0+40, отражаемый в клетке (100, 0). 2) второму проекту может быть выделено х2 = 100 тыс. руб., прирост продукции при втором проекте составляет f2 (100) = 50 тыс. руб. В этом случае значение функции Беллмана из табл. 1 составит F 3(100 – 100) = F 3(0) = 0, т.е. вся сумма C2 = 100 тыс. руб. выделена второму проекту, поэтому суммарный прирост продукции составит 50+0, отражаемый в клетке (100, 100). Рассуждая аналогично, заполняются все строки табл. 2. Максимальная сумма по каждой строке вносится в колонку F 2(C 2), одновременно в колонку Например, в строке C2 = 100 максимальная сумма 160 не единственная, следовательно, F 2(100) = 50, ему соответствует значение х2 = 100, следовательно,
3-й шаг: k = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими проектами, используя следующую формулу для расчета суммарного дохода:
В шапке таблицы отражены варианты значений капиталовложений х1, которые могут быть предоставлены первому проекту при условии, что часть средств выделяется второму и третьему проекту. В клетках таблицы первое слагаемое – это возможный прирост выпуска продукции при первом проекте f1 (х1) в результате освоения капиталовложений х1; второе слагаемое – значение функции Беллмана, полученной на предыдущем шаге F 2(C1 – х1), т.е. возможный прирост выпуска продукции при втором и третьем проектам, если им будет выделена оставшаяся часть капиталовложений, определяемая как C1 – х1. Таблица 3
Значение функции Беллмана F 1(С 1) представляет собой максимально возможный доход при всех проектах, а значение Значение целевой функции равно максимальному значению функции Беллмана F 1(С 1) из табл. 3. Следовательно, значение целевой функции равно F max(x*) = 240 тыс. руб. II этап. Безусловная оптимизация. Далее на этапе безусловной оптимизации для всех последующих шагов вычисляется величина Сk = (Сk -1 – хk -1) оптимальным управлением на k -м шаге является то значение хk, которое обеспечивает максимум дохода при соответствующем состоянии системы Sk. Определяем компоненты оптимальной стратегии. Для этого значения функций Беллмана и соответствующие им оптимальные значения х вносим в итоговую табл. 4. Таблица 4.
1-й шаг. По данным из табл. 4 максимальный доход при распределении 700 тыс. руб. между тремя проектами составляет: C 1 = 700, F 1(700) = 240 тыс. руб. При этом возможны следующие варианты. Первому проекту нужно выделить: 1) 2) 2-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего проектов: 1) С 2 = C 1 – 2) С 2 = C 1 – По данным табл. 4 находим, что оптимальный вариант распределения между вторым и третьим проектами денежных средств размером: 1) 200 тыс. руб. составляет: F 2(200) = 90 тыс. руб. при выделении второму проекту 2) 100 тыс. руб. составляет: F 2(100) = 50 тыс. руб. при выделении второму проекту 3-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего проекта: 1) С 3 = C 2 – 2) С 3 = C 2 – По данным табл. 4 находим: 1) F 3(100) = 40 и 2) F 3(0) = 0 и
Таким образом, возможны два альтернативных варианта оптимального плана инвестирования проектов: 1) х * = (500, 100, 100), который обеспечит максимальный доход, равный F (700) = f1 (500) + f2 (100) + f3 (100) = 150 + 50 + 40 = 240 тыс. руб.; 2) х ** = (600, 100, 0), который обеспечит максимальный доход, равный F (700) = f1 (600) + f2 (100) + f3 (0) = 190 + 50 + 0 = 240 тыс. руб. Заключение. Подвести итог о том, что в работе исследовано и что получено.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.146 (0.042 с.) |
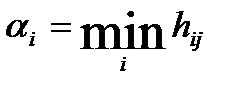

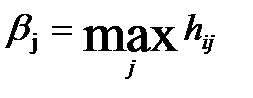
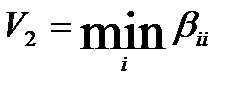
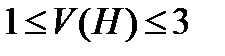

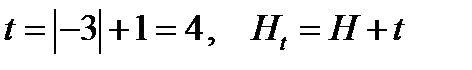 .
.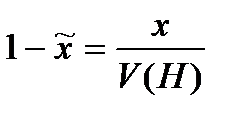 , для игрока
, для игрока 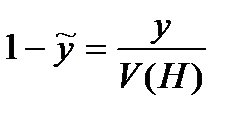 .
.





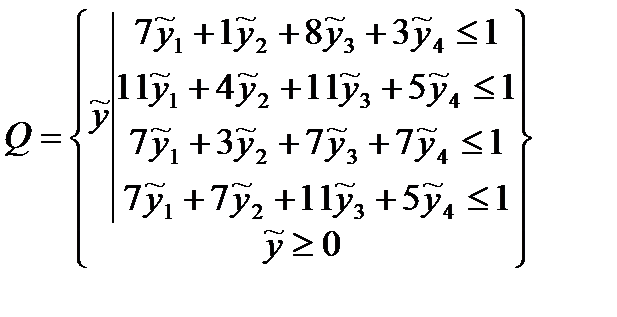




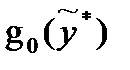
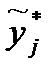
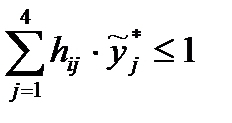
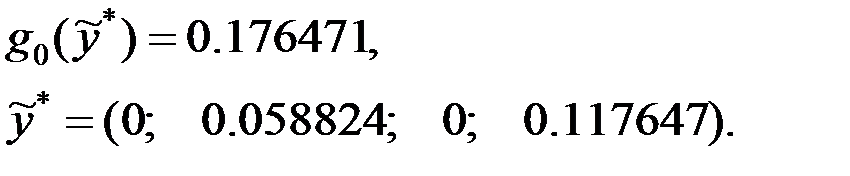

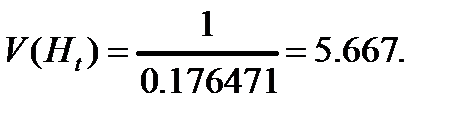
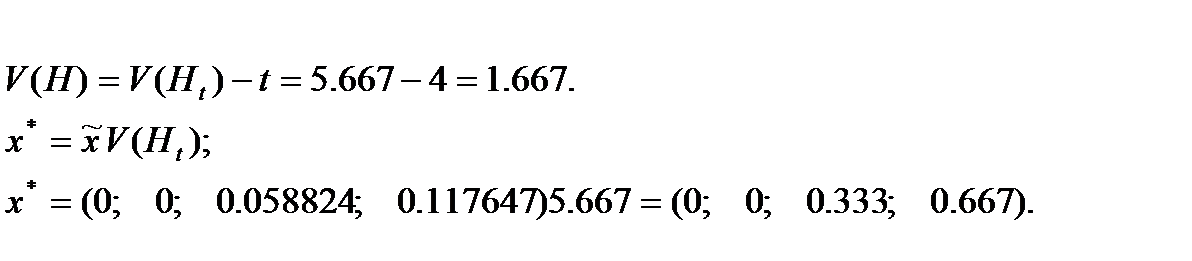

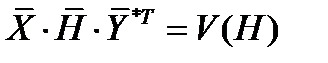
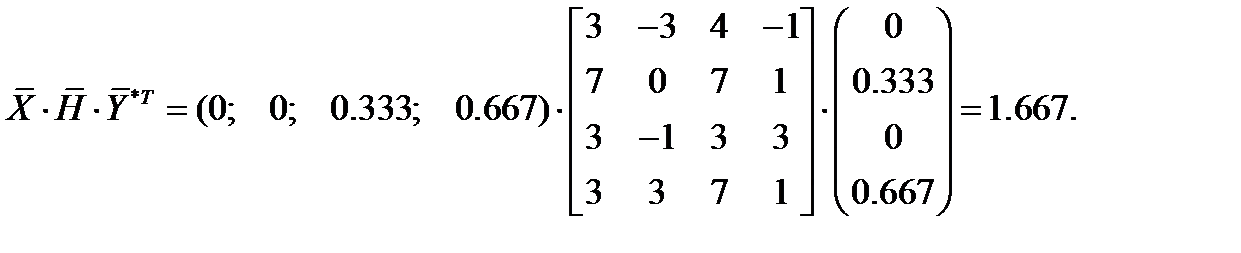
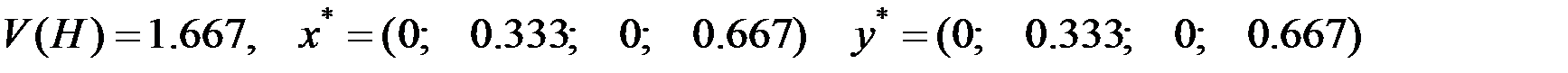
 ,
,  , n – количество проектов, m – количество возможных сумм капитальных вложений.
, n – количество проектов, m – количество возможных сумм капитальных вложений.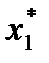 ,
, 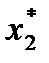 , …,
, …, 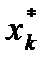 , …,
, …, 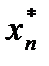 ), обеспечивающий максимум целевой функции
), обеспечивающий максимум целевой функции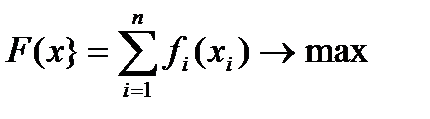
 ,
,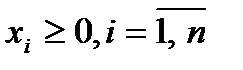

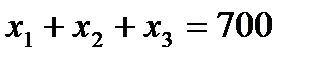 ,
,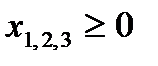 .
.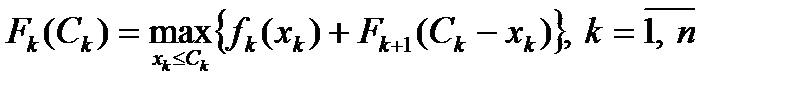 ,
,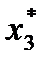
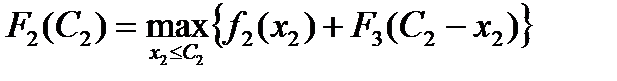 .
.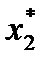
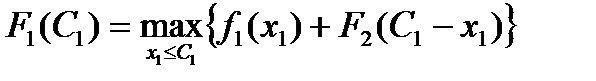 , на ее основе составлена табл. 3.
, на ее основе составлена табл. 3.
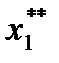 = 600 тыс. руб.
= 600 тыс. руб. = 100 тыс. руб.;
= 100 тыс. руб.;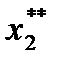 = 100 тыс. руб.
= 100 тыс. руб. = 200 – 100 = 100 тыс. руб.;
= 200 – 100 = 100 тыс. руб.; = 100 тыс. руб.;
= 100 тыс. руб.;


