Хвост списка всегда есть список; голова списка есть элемент.

Если многократно отнимать первый элемент от хвоста списка, мы получим в конечном итоге пустой список ( [ ] ).

Пустой список не может быть разбит на голову и хвост.

Операция разделения списка на голову и хвост обозначается с помощью вертикальной черты:

[Head|Tail] [Голова|Хвост]

 

С помощью этой операции можно реализовывать рекурсивную обработку списка. Например, если мы хотим напечатать все элементы списка из программы на рис. 4.1 построчно, то это можно выполнить с помощью рекурсивного определения предиката:

print_list([ ]).

print_list([X|Y]):- write(X), nl, print_list(Y).

Для описания предиката печати можно использовать конструкцию:

show:- dogs(X), print_list(X).

Практикум 4-1

:	Напишите программу, хранящую увлечения студентов в виде списков. hobby("Маша", [теннис, музыка]). hobby("Коля", [музыка, еда, компьютер]). hobby("Вася", [лыжи, еда, компьютер, футбол]). Результат напечатайте в виде, представленном на рис. 4.3

Рис. 4.3. Результаты программы Практикума 4-1

 

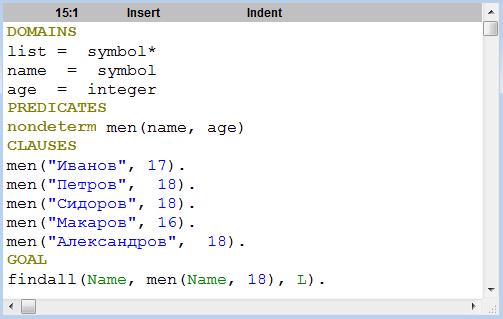
Встроенный предикат findall

При формировании списка из данных, содержащихся в виде фактов в базе данных или непосредственно в программе, полезным оказывается предикат findall. Он собирает значения, получаемые в процессе бектрекинга, в список. Формат предиката:

findall(Переменная, Предикат, Список),

где первый аргумент определяет параметр, который необходимо собрать в список, второй аргумент определяет предикат, из которого фор­мируется список значений, третий аргумент - формируемый список.

На рис. 4.4 представлена программа, выводящая в список мужчин 18 лет.

Рис. 4.4. Пример использования предиката findall

 

В результате получим список

L= [“Петров”, “Сидоров”, “Александров”].

Практикум 4-2

:	В программу, представленную на рис. 4.4. добавьте факты. С помощью предиката findall получите список всех мужчин призывного возраста (от 18 до 27 лет)

 

Рассмотрим обработку списков. Поскольку списки являются в действительности рекурсивными составными структурами данных, для их обработки необходимы и рекурсивные алгоритмы. Самый естественный способ обработки списков - сквозной просмотр, в ходе которого что-то делается с каждым элементом, до тех пор, пока не достигнут конец.

Как правило, такого рода алгоритмы используют процедуру, состоящую из двух правил. Одно из них говорит о том, как поступать с обыкновенным списком, который может быть разделен на голову и хвост. Другое говорит о том, что делать с пустым списком.

 

Вычисление длины списка

Создадим предикат, позволяющий вычислить длину списка, т.е. количество элементов в списке.

 

Для решения этой задачи воспользуемся очевидным фактом, что

· длина пустого списка [] есть 0.

· длина любого другого списка есть 1 плюс длина его хвоста.

Запишем эту идею:

Рис. 4.5. Вычисление длины списка

Обратите внимание, что при переходе от всего списка к его хвосту нам неважно, чему равен первый элемент списка, поэтому мы используем анонимную переменную.

Разберем на примере, как это будет работать. Пусть нас интересует количество элементов в списке [1,2,3]. Запишем соответствующий вопрос Пролог-системе:

length([1,2,3],X).

Система попытается вначале сопоставить нашу цель с первым предложением length([], 0), однако ей это не удается сделать, потому что первый аргумент цели является непустым списком. Система переходит ко второму предложению процедуры. Сопоставление с заголовком правила проходит успешно, переменная X связывается с переменной L, список [1,2,3] будет сопоставлен со списком [_|T], переменная T будет конкретизирована значением [2,3]. Теперь система переходит к попытке достижения подцели length(T,L_T). Как и в предыдущем случае, первое предложение с подцелью не сопоставляется, так как список T не пустой. При сопоставлении заголовка правила с подцелью хвост T конкретизируется одноэлементным списком [3]. На следующем шаге рекурсии переменная T означена пустым списком (хвост одноэлементного списка). И, значит, наша подцель выглядит следующим образом: length([], L_T). Эта цель сопоставляется с фактом, переменная L_T становится равной нулю. Раскручивается обратный ход рекурсии: переменная L_T увеличивается на единицу, результат попадает в переменную L. Получаем, что длина списка [3] равна единице. На следующем обратном шаге происходит еще одно добавление единицы, после чего длина списка [2,3] конкретизируется двойкой. И, наконец, на последнем возвратном шаге получаем означивание переменной L числом 3 (количеством элементов в списке [1,2,3]).

Пошаговая трассировка программы представлена в таблице 4.1

Таблица 4.1

	Шаг программы	Проверка	Результат
	Цель сопоставляется с первым предложением	length([1,2,3],X)== length([ ], 0)?	ложь
	Цель сопоставляется со вторым предложением	length([1,2,3],X)==length([ _|T], L)? это точка возврата	Т=[2,3] L – заносим в стек
	Первая подцель во втором предложении	length([2,3], L1)? это точка возврата	L1 – заносим в стек
	сопоставляется с первым предложением	length([2,3],X)== length([], 0)?	ложь
	сопоставляется со вторым предложением	length([2,3],X)==length([_|T], L)	Т=[3]
	Первая подцель во втором предложении	length([3], L1)? это точка возврата	L1 – заносим в стек
	сопоставляется с первым предложением	length([3],X)== length([], 0)?	ложь
	сопоставляется со вторым предложением	length([3],X)==length([_|T], L)?	Т=[]
	Первая подцель во втором предложении	length([ ], L1)? это точка возврата	L1 – заносим в стек
	сопоставляется с первым предложением	length([],X)== length([], 0)?	истина X=0
	возврат к шагу 9	Первая подцель во втором предложении length([ ], L1)? Истина	L1=0
	вторая подцель во втором предложении	L = L1 + 1	L=1
	возврат к шагу 6	Первая подцель во втором предложении length([3], L1)? Истина	L1=1
	вторая подцель во втором предложении	L = L1 + 1	L=2
	возврат к шагу 3	Первая подцель во втором предложении length([2,3], L1)? Истина	L1=2
	вторая подцель во втором предложении	L = L1 + 1	L=3
	возврат к шагу 2	length([1,2,3],X)==length([_|2,3], 3)?	X=3

Практикум 4-3