Использование предиката fail

В Прологе реализован механизм поиска с возвратом (backtracking), при котором система пытается отыскать все возможные решения задачи. Механизм вывода программы запоминает те точки процесса унификации, в которых не были использованы все альтернативные решения, а затем возвращается в эти точки и ищет решение по иному пути.

При наличии нескольких фактов, поиск заканчивается после нахождения первого решения задачи. Например [3], в программе на рис. 3.1 находит только первое решение и заканчивает работу.

Рис.3.1. Пример нахождения одного решения

 

Если же нужно найти все решения, то в этом случае используется предикат fail. Предикат fail всегда дает неудачу в доказательстве, он вызывает искусственное неуспешное завершение поиска, что позволяет получить все возможные решения задачи и, таким образом, поддерживает поиск с возвратом.

Обратите внимание, что помещать подцель после fail в теле правила бесполезно. Предикат fail все время завершается неудачно, нет возможности для достижения подцели, расположенной после fail.

Рис 3.2. Пример программы с использованием предиката fail

После запуска программы, представленной на рис 3.2, будут напечатаны все названия городов.

Практикум 3-1

:

В Практикуме 2-1 Вы создавали базу знаний (БЗ), хранящую сведения о студентах (не менее 10) и их средних баллах. 1. Создайте предикат, выводящий на экран всех студентов. 2. Создайте предикат, выводящий на экран всех студентов со средним баллом от 3 до 4. Для решения задач воспользуйтесь встроенным предикатом fail. Какой результат выводится, если убрать предикат fail из правил?

 

Использование предиката cut

Предикат отсечения[1] «cut» обозначается с помощью символа!. Он позволяет получить доступ только к части данных, устраняя дальнейшие поисковые действия. В общем виде можно записать, например:

R: – A,B,!, C.

Это означает, что если для целей А и В найдено хотя бы одно решение, то дальнейший перебор возможных вариантов значений А и В не нужен.

Когда процесс проходит через отсечение, выполняется обращение к очередной подцели (если таковая имеется). Пройдя через отсечение, уже невозможно произвести откат к подцелям, расположенным в обрабатываемом предложении перед отсечением, и также невозможно возвратиться к другим предложениям, определяющим обрабатывающий предикат (предикат, содержащий отсечение).

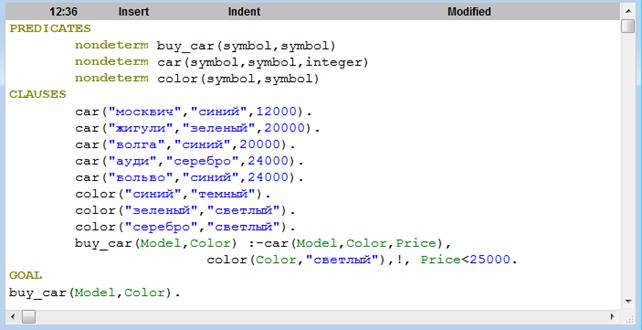
Существуют два основных случая применения отсечения.

· Если заранее известно, что определенные посылки никогда не приведут к осмысленным решениям (поиск решений в этом случае будет лишней тратой времени), Отсечение позволяет сделать программу быстрее и экономичнее. Такой прием называют зеленым отсечением.

· Если отсечения требует сама логика программы для исключения из рассмотрения альтернативных подцелей. Это - красное отсечение.

Таким образом, зеленое отсечение не меняет семантики предиката, в котором оно используется. Красное отсечение, наоборот, меняет семантику. Для того чтобы определить цвет отсечения, необходимо удалить его из программы и посмотреть, как программа отвечает на поставленные вопросы, также, как программа без отсечения или по-другому. Как правило, различия проявляются, если в запросах использовать переменные.

На рис. 3.3 приведена программа, составляющая все возможные пары мальчик+девочка.

Рис 3.3. Пример программы без отсечения

Практикум 3-2

:	1. Проверьте работу программы, приведенной на рис.3.3. 2. Проверьте, как изменятся результаты, если в предикат show вставлять предикат отсечения: Объясните каждый из получившихся результатов. Определите в каждом случае цвет отсечения

Отсечение - это мощный, но и опасный оператор Пролога: он многое позволяет, но делает программу более трудной для понимания.

 

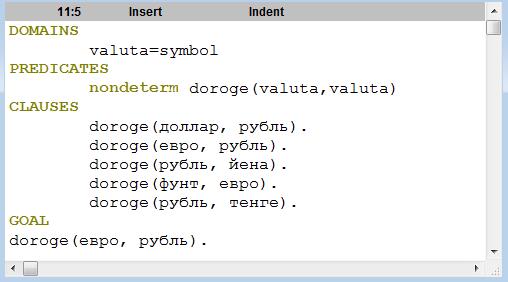
Использование рекурсии

Правило является рекурсивным, если содержит в качестве компоненты само себя. Рекурсия допустима в большинстве языков программирования, но там этот механизм не является таким важным, поскольку имеются другие, свойственные процедурным языкам, механизмы – циклы, процедуры и функции.

Рассмотрим преимущества использования рекурсии на примере.

Пусть имеются следующие факты о том, какая валюта котируется выше (рис.3.4):

Рис 3.4. Пример программы

Результатом запроса на рис.3.4 будет yes, потому что такой факт явно описан в программе.

Если же сделать запрос,

GOAL

doroge(евро, йена).

или

doroge (фунт, рубль).

 

То ответ будет отрицательный (no), поскольку такие факты отсутствуют.

Избежать противоречий здесь можно введением правила, в котором допустимо сравнение между собой не только двух, но и трех объектов:

doroge_3(X, Y):- doroge(X, Y). /* два объекта */

doroge_3(X, Y):- doroge(X, Z), doroge(Z, Y). /* три объекта */

Второе правило описывает правило транзитивности, если X>Z, и Z>Y, то делается вывод, что X>Y.

Однако цепочка взаимных сравнений может быть более длинной. Например, при четырех сравнениях потребуется конструкция:

doroge_4(X, Y):- doroge(X, M), doroge(M, K), doroge(K, Z), doroge(Z, Y).

Описывать такие длинные правила неудобно. Здесь выгоднее применить рекурсию, обратившись к правилу из самого этого правила:

val_doroge(X, Y):- doroge(X, Y).

val_doroge(X, Y):- doroge(X, Z), val_doroge(Z, Y).

 

Первое предложение в этой конструкции определяет момент прекращения рекурсивных вызовов, если существует такой факт.

Второе правило описывает возможности рекурсивных вызовов, когда существуют варианты решения, выводимые логичски.

Практикум 3-3

:	Проверьте, как работает программа c рекурсией (с фактами о том, какая валюта котируется выше, рис.3.4), получите ответы на вопросы – выбрать все валюты, которые котируется выше рубля, – выбрать все валюты, которые котируется ниже рубля.

 

Любая рекурсивная процедура должна включать в себя базис и шаг рекурсии.

Базис рекурсии - это предложение, определяющее некую начальную ситуацию или ситуацию в момент прекращения

Шаг рекурсии – это рекурсивное правило, имеющее подцель, которая вырабатывает новые значения аргументов, и рекурсивную подцель, которая использует вычисленные значения.Во избежание зацикливания, определяемый предикат должен вызываться не от тех же параметров, которые указаны в заголовке правила. Параметры должны изменяться на каждом шаге так, чтобы в итоге либо сработал базис рекурсии, либо условие выхода из рекурсии, размещенное в самом правиле.

База правил просматривается всегда сверху вниз. Сначала делается попытка выполнения нерекурсивной фразы (базиса). Если условие окончания рекурсии не указано, то правило может работать бесконечно.

Например:

write_string:- write(“*****”),nl, write_string.

будет бесконечно печатать звездочки на экране компьютера.

Рассмотрим применение рекурсии на примере вычисления факториала натурального числа N!=1*2*3*…*N. Рекурсивная математическая запись:

1!=1 N!=(N-1)!*N

На рис. 3.5 представлена программа вычисления факториала, однако эта программа не будет работать правильно, а будет вызывать бесконечный цикл и переполнение памяти. Это происходит потому, что в программе произошел выход в отрицательную часть целых чисел, что не было предусмотрено формулой, на которой была основана эта процедура.

 

Рис 3.5. Пример неправильной программы

 

Для исправления этой ошибки возможны два варианта

1. Можно проверить, что число, для которого применяется правило, больше единицы (рис. 3.6-а).

2. Добавить в первое предложение (в базис рекурсии) отсечение. При достижении истинности высказывания, предложения процедуры, расположенные ниже той, из которой оно было вызвано, не рассматриваются (рис.3.6-б)

а)

б)

Рис 3.6. Примеры исправления программы

Практикум 3-4

:	Проверьте, как работает программа вычисления факториала, добавив вывод промежуточных результатов с помощью предикатов write("N1=",N1) после вычисления N1 и write("N1=",N1," F1=",F1) после вычисления fact(N1,F1).

 

Программа, представленная на рис. 3.7. должна печатать на экране компьютера цифры от 1 до 10.

Рис 3.7. Программа печати чисел

Практикум 3-5

:	а) Проверьте, действительно ли программа, представленная на рис. 3.7 печатает числа от 1 до 10? Исправьте программу, чтобы она работала правильно. б) Создайте программу печати чисел в обратном порядке от 10 до 1.

Программа, представленная на рис. 3.8 печатает сумму всех цифр введенного с клавиатуры числа.

 

Рис 3.8. Программа вычисления суммы цифр целого числа

Использование предиката! в описании базиса рекурсии позволяет избежать здесь переполнения стека.

Практикум 3-6

:	а) Проверьте, действительно ли программа, представленная на рис. 3.8 правильно считает сумму цифр. б) Создайте программу перевода десятичного числа в двоичное. (Двоичное число можно представить как строку из 0 и 1)

 

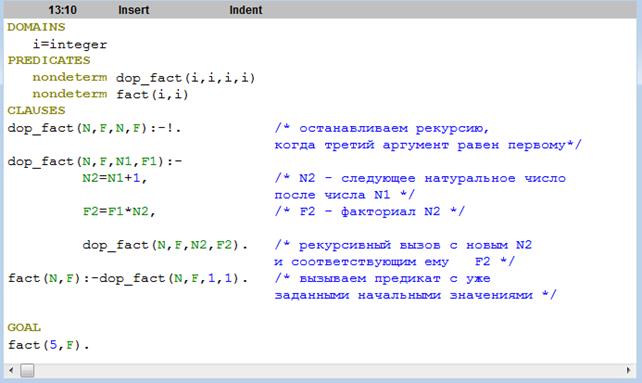
Хвостовая рекурсия

При каждом рекурсивном вызове предиката в специальном стековом фрейме запоминаются все промежуточные переменные, которые могут понадобиться. При больших входных значениях, т.е при большом количестве рекурсивных циклов, объема стека может не хватить. Этот недостаток рекурсии может быть исправлен использованием «хвостовой» или правой рекурсии. В этом варианте рекурсия использует практически столько же оперативной памяти, сколько итерация в императивных языках программирования.

Для ее осуществления рекурсивный вызов определяемого предиката должен быть последней подцелью в теле рекурсивного правила и к моменту рекурсивного вызова не должно остаться точек возврата (непроверенных альтернатив). То есть у подцелей, расположенных левее рекурсивного вызова предиката, не должно оставаться каких-то непроверенных вариантов и у процедуры не должно быть предложений, расположенных ниже рекурсивного правила.

Пример. На рис. 3.9. представлен пример использования хвостовой рекурсии для вычисления факториала.

Вычисления осуществляются с помощью дополнительного предиката, в который передаются исходные данные и начальные значения. В дополнительном предикате третий параметр – это натуральные числа 1, 2, …, N, а в четвертом последовательно вычисляются значения 1!, 2!, …, N!

Процесс останавливается, когда третий параметр достигнет значения N.

Рис 3.9. Программа вычисления N! с использованием хвостовой рекурсии

 

Практикум 3-7

:	С использованием хвостовой рекурсии вычислить Y=X^N

Самостоятельные задания

1. На рис. 3.10 представлен пример Пролог - программы. Какого цвета использовано отсечение – красное или зеленое?

Рис 3.10. Программа с использованием отсечения

2. Даны а,n. Вычислить S=a+a²+a³+…+aⁿ

3. Даны а,n. Вычислить S=a+a(a+1)+a(a+1)(a+2)+…+a(a+1)*…*(a+n)

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4.

Понятие списков в Прологе

 

Списки – одна из наиболее часто употребляемых структур в Прологе. Список – это объект, содержащий внутри произвольное число других объектов. Списки соответствуют, грубо говоря, массивам в других языках, но, в отличие от массивов, список не требует декларирования его размера до начала его использования.

При записи список заключают в квадратные скобки, а элементы списка разделяют запятыми, например:

[1,2,3]

[1.1,1.2,3.6]

[“вчера”,”сегодня”,”завтра”]

Элементами в списке может быть что угодно, включая другие списки, но все элементы в списке должны принадлежать одному домену.

В Прологе списки должны быть обязательно объявлены в разделе domains. Для этого необходимо ввести имя нового домена и определить домен, который описывает тип элементов, объединяемых в список (в качестве такого домена можно использовать стандартные домены).

В разделе описания доменов списки описываются следующим образом:

domains

<имя спискового домена>=<имя домена элементов списка>*

Звездочка после имени домена указывает на то, что мы описываем список, состоящий из объектов соответствующего типа.

 

Например:

domains

list_integer = integer* /*вводится домен списка целых чисел */

list_s = symbol* /* вводится домен списка символов*/

list_list = list_s* /* элементами этого списка должны быть списки символов*/

 

Например: num([1,2,3]).

Пусть мы хотим описать с помощью списка породы собак (рис. 4.1).

Рис. 4.1. Пример программы со списком

В результате выполнения запроса, представленного на рис. 4.1, запроса будут напечатаны все породы собак, а после запроса:

получим:

 

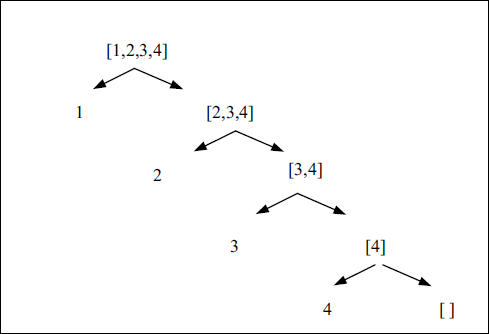
Каждый непустой список может быть разделен на голову – первый элемент списка и хвост – остальные элементы списка. Это позволяет всякий список представить в виде бинарного дерева (рис. 4.2).

Рис. 4.2. Представление списка в виде бинарного дерева

 

У списка, состоящего только из одного элемента, головой является этот элемент, а хвостом – пустой список.