
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 5. Router. Управление потоками данных в локальной сети.Содержание книги
Поиск на нашем сайте
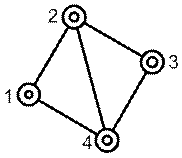
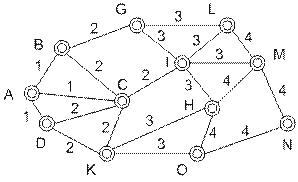
Теоретические основы. Маршрут (route) – список элементов сети связи (узлов коммутации ук, линий связи, каналов связи), начинающийся с узла-источника (уи) и заканчивающийся узлом-получателем (уп). 1. Маршруты между ук №1 и ук №4 на сети, изображенной на рисунке 5.1, будут иметь следующую запись: Μ11,4 = {ук № 1, ук № 4}; Μ21,4 = {ук № 1, ук № 2, ук № 4}; Μ31,4 = {ук № 1, ук № 2, ук № 3, ук № 4}. В данном примере ук № 1 является исходящим, ук № 4 – входящим, а ук № 2, 3 – транзитными.
Рисунок 5.1 – Пример структуры сети связи Маршрутизация (routing) – процедура, определяющая оптимальный по заданным параметрам маршрут на сети связи между узлами коммутации. Для реализации маршрутизации на сети в каждом транзитном ук (ук № j), начиная с уи, формируется таблица маршрутизации,которая представляет собой матрицу размерностью (s – 1) x hj
Где s – количество ук в сети; hj – количество исходящих линий связи (лс) из j-го ук. матрица m(j) содержит информацию о предпочтительности выбора исходящей лс из j-го ук при поиске маршрута к i-му узлу (уп). первый элемент mi1(j) вектор-строки (5.2) указывает номер исходящей лс из j-го ук к смежному ук, которую предпочтительнее выбрать для организации маршрута к i-му ук (уп). второй элемент (5.2) указывает номер следующей исходящей лс из j-го ук к другому смежному ук, которая менее предпочтительна для организации искомого маршрута. И так до hj-го элемента вектор-строки (5.2). в данном случае: mi1(j) – исходящая лс hj-го выбора. 2. Построим таблицу маршрутизации для ук № 2 (рисунок 5.1). Соответствующие строки матрицы m(2) будут иметь следующий вид:
при поиске маршрута от ук № 2 к ук № 1 необходимо обратиться к вектор-строке 3. Зададим при на сети, изображенной на рисунке 5.1:
в данном примере формирование при осуществлялось по минимальному количеству транзитных ук в искомом маршруте. Возможны ситуации, когда формирование при осуществляется и по другим критериям: ¾ Надежность элементов сети связи; ¾ Время задержки передачи информации в элементах сети; ¾ Скорость передачи информации и прочие. ¾ Данные параметры являются случайными величинами и зависят от многих причин: ¾ Вида и интенсивности трафика пользователей сети; ¾ Условий окружающей среды при эксплуатации оборудования сети; ¾ Технического состояния оборудования сети и других причин. Поэтому в процессе эксплуатации сетей связи могут возникнуть ситуации, при которых необходимо скорректировать таблицы маршрутизации и тем самым переформировать. Если в процессе эксплуатации сетей связи происходит автоматическое переформирование при (без участия администрации сети), то такой при называют динамическим. Иначе формирование при будет статическим. При позволяет определить маршруты между любой парой узлов на сети связи. Для этого необходимо во всех транзитных ук, начиная с уи, обращаясь к таблице маршрутизации, выбрать вектор-строку, номер которой совпадает с номером уп. В данной вектор-строке необходимо выбрать исходящую лс первого выбора. Если исходящая лс первого выбора оказалась недоступной (занятость передачей другой информации или неисправность аппаратуры), то следует выбрать исходящую лс второго выбора. В случае недоступности исходящей лс второго выбора необходимо выбрать следующую по предпочтительности исходящую лс. Данная процедура продолжается во всех узлах, участвующих в формировании искомого маршрута, пока не будет определен маршрут между заданной парой узлов. В случае недоступности всех исходящих лс в данном узле потребуется либо вернуться на предыдущий ук и выбрать менее предпочтительную исходящую лс, либо дать отказ на невозможность организации искомого маршрута между заданной парой узлов. Таким образом, анализируя процедуры, участвующие в формировании маршрутов можно заключить, что маршрутизация состоит из двух этапов:
Протоколы, реализующие формирование и коррекцию при (формирование таблиц маршрутизации), часто называют протоколами маршрутизации. Протоколы, отвечающие за выбор исходящих лс в ук (формирование таблиц коммутации), – протоколами сигнализации. Маршрутизация и модель вос. В модели вос функции маршрутизации возложены на третий – сетевой уровень (network layer). Данный уровень удобно представить в виде подуровней (рисунок 5.2). На третьем, верхнем подуровне производится формирование.
Рис. 5.2 – подуровни сетевого уровня модели ВОС. Администрацией при проектировании или модификации сети связи. Частота коррекции при зависит от многих факторов: ¾ Использование статических или динамических методов маршрутизации; ¾ Набора статистики (за определенный период времени) о состоянии элементов сети связи (неисправность и перегруженность); ¾ Степени централизации устройств управления сетью связи (централизованные, децентрализованные или комбинированные методы управления); ¾ Возможности администрации влиять на процесс управления сетью связи; ¾ Наличие постоянных (не коммутируемых) соединений между пользователями сети связи. Сформированные таблицы маршрутизации для каждого ук передаются на второй подуровень. На втором подуровне решается задача определения и выбора (в каждом транзитном ук, начиная с уи) исходящих лс. Вызывающий пользователь сети инициирует пакет вызова на установление соединения с вызываемым пользователем. Пакет вызова, проходя через узлы коммутации, обращается к таблицам маршрутизации, которые сформированы на третьем подуровне. Затем пакет вызова определяет исходящие лс. Таким образом, в каждом транзитном ук, начиная с уи, формируются таблицы коммутации. В таблице коммутации указываются конкретные исходящие лс, участвующие в формировании маршрута между вызывающим и вызываемым пользователями. Сформированные таблицы коммутации передаются на первый подуровень. В данном подуровне в соответствии с таблицами коммутации происходит передача сообщения по маршруту, сформированному на втором подуровне.
Методы формирования плана распределения информации на сети связи (таблиц маршрутизации). Метод рельефов. Суть данного метода состоит в следующем. Пусть i – произвольный ук сети связи. I–рельефом называется процедура присвоения значения числовой функции каждой лс. I–рельеф строится следующим образом. Из i-го ук по всем исходящим лс передается число 1. Все ук, в которые поступило число 1, передают по всем исходящим лс, кроме тех лс, по которым поступила 1, число 2. Далее ук, на которые поступило число 2, передают по лс, кроме тех, по которым поступила 2, число 3 и т.д., до тех пор, пока все лс не будут пронумерованы. Говорят, что лс имеет n высоту, если она обозначена числом n в i–рельефе. Указанным способом формируется рельеф из каждого ук сети связи. В итоге получается, что каждая лс имеет s высот. В результате лс с минимальной высотой является исходящей лс первого выбора. Лс с большими высотами, соответственно, являются исходящими лс второго, третьего и т.д. Выбора. 4. Построим рельеф на сети относительно ук а (рисунок 5.3). Ук а по исходящим лс ав, ас, аd передает число 1 и присваивает им это значение. Узлы b, c и d передают по лс вg, вс, сi, ск, сd и dк в узлы g, i и к число 2. В свою очередь, узлы g, i, н и к передают по лс gl, gi, il, im, ih, hk и ко число 3. Перечисленным лс присваивается число 3. Ук l, м, н, о, в свою очередь, передают по лс lm, мn, нм, но и оn число 4 и им присваивается число 4. Таким образом, на сети строится а-рельеф (рисунок 5.4). Чтобы найти кратчайший маршрут от произвольного ук к узлу а достаточно в каждом ук выбирать исходящую лс с меньшим весом. Например, кратчайший маршрут от ук n до ук а будет следующий: Недостатком данного метода является необходимость передачи информации при формировании рельефов между всеми узлами. Игровой метод формирует при по накопленной ранее статистике установления соединения между заданной парой ук. Перед началом функционирования на сети устанавливается начальный при в виде набора таблиц маршрутизации (5.1). Каждому значению В результате формируется матрица весовых коэффициентов
Где
Определение маршрута и формирование при на сети игровым методом осуществляется следующим образом. Во всех транзитных ук, начиная с уи, при поиске маршрута к i-му уп происходит обращение к i-м строкам матриц маршрутизации (5.4). В i-х строках (5.5) определяется максимальный весовой коэффициент Критерием оптимальности является результат организации маршрутов. 5. Покажем формирование при игровом методом для сети, изображенной на рисунке 5.1. Будем считать, что начальный при задан в виде таблиц маршрутизации примера 5.3. Весовые коэффициенты (5.4) для узлов сети имеют следующий вид:
Допустим, что необходимо определить маршрут между уи №2 и уп №1, при условии, что количество транзитных ук не должно превышать одного. В уи № 2 из таблицы весовых коэффициентов р(2) выбираем вектор-строку Если ситуация поиска маршрута между заданной парой ук повторится, то вектора Матрицы весовых коэффициентов ук № 2 и 4 примут следующий вид:
Если рассматривать весовые коэффициенты Отсутствие необходимости передачи служебной информации при формировании при на сети является несомненным достоинством игрового метода. Однако данный метод обладает инерционностью. Действительно, при выходе элементов сети связи из строя потребуется некоторый период времени для переформирования при на сети. Логический метод состоит в процедуре, выполняемой в каждом транзитном ук, начиная от уи, позволяющей определить исходящую лс, максимально близкой к геометрическому направлению на уп. Сеть связи вкладывается в прямоугольную систему координат. Каждому узлу сети присваивается собственный адрес (x, у) (рисунок 5.5).
В каждом транзитном ук (xi, yj), начиная с уи (xr, yl), производится анализ адреса уп сопоставлением его с собственным. В результате вычисляется геометрическое направление из данного узла на уп. Затем определяется та лс, которая имеет наибольшее совпадение с ранее рассчитанным геометрическим направлением на уп. Если ближайшая по направлению исходящая лс не доступна, то подбирается очередная по предпочтительности исходящая лс.
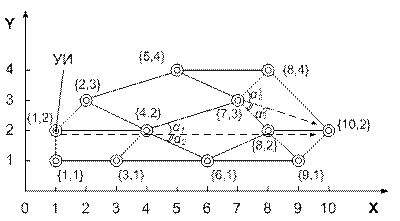
6. На рисунке 5.6 представлена сеть связи, в которой уи и уп, соответственно, имеют координаты {1, 2} и {10, 2}. Из уи определяем геометрическое направление на уп (указано пунктиром). С данным направлением совпадает исходящая лс к узлу с координатами {4, 2}. В ук {4, 2} выбираем исходящую лс к ук с координатами {7, 3}, так как она имеет наименьший угол отклонения от геометрического направления на уп. В ук {7, 3} подобным образом выбираем лс к ук {8, 2}. В ук {8, 2} выбираем лс к ук {10, 2}.
Таким образом: Логически-игровой метод формирования при является обобщением логического и игрового методов. По аналогии с логическим методом сеть связи вкладывается в прямоугольную систему координат, в соответствии с которой каждому узлу сети присваивается собственный адрес (x, у). В каждом ук j имеется матрица Табл.5.1 – Матрица значений весовых коэффициентов
И содержит s0 строк. Учитывая, что возможно увеличение числа ук на сети, то s0 выбирают таким, чтобы s0>s. Количество столбцов матрицы p0(j) для ук под номером j равно: (нj+3), где нj – число исходящих лс из j-го узла; три столбца отводится для номеров уп, представленных в общепризнанной нумерации и прямоугольной системе координат (x, у). На момент ввода узла в эксплуатацию матрица содержит только информацию о смежных номерах ук с данными выраженных в прямоугольной системе координат: (хqj, уqj),..., (xvj, уvj),..., (хhj, уhj). По мере функционирования сети связи матрица р0(j) заполняется и корректируется. Определение исходящих лс осуществляется логическим методом, а заполнение и корректировка матрицы p0(j) осуществляется игровым методом.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.41 (0.013 с.) |

 (5.1)
(5.1) (5.2)
(5.2)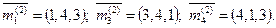 (5.3)
(5.3)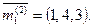 исходящая лс к ук № 1 является более предпочтительной, так как она ведет непосредственно к искомому ук, следовательно, является исходящей лс первого выбора. Соответственно, исходящие лс к ук №4 и 3 являются исходящими лс второго и третьего выбора. Для того, чтобы была возможность определять маршруты между любой парой ук необходимо построить таблицы маршрутизации в каждом узле сети. Совокупность таблиц маршрутизации для всех ук называется планом распределения информации (при) на сети связи.
исходящая лс к ук № 1 является более предпочтительной, так как она ведет непосредственно к искомому ук, следовательно, является исходящей лс первого выбора. Соответственно, исходящие лс к ук №4 и 3 являются исходящими лс второго и третьего выбора. Для того, чтобы была возможность определять маршруты между любой парой ук необходимо построить таблицы маршрутизации в каждом узле сети. Совокупность таблиц маршрутизации для всех ук называется планом распределения информации (при) на сети связи.

 или
или 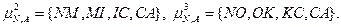
 присваивается некоторый весовой коэффициент
присваивается некоторый весовой коэффициент 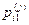 . Причем,
. Причем, 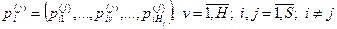 нормируется
нормируется 
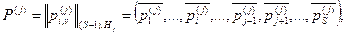 (5.4)
(5.4) (5.5)
(5.5)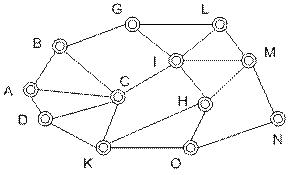
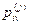 . Тем самым выбирается v-я исходящая лс из j-го ук при организации маршрута к i-му ук. В результате данных действий маршрут между заданной парой ук будет либо определен, либо данной заявке на определение маршрута будет дан отказ. В первом случае все лс, входящие в данный маршрут, поощряются. Весовые коэффициенты
. Тем самым выбирается v-я исходящая лс из j-го ук при организации маршрута к i-му ук. В результате данных действий маршрут между заданной парой ук будет либо определен, либо данной заявке на определение маршрута будет дан отказ. В первом случае все лс, входящие в данный маршрут, поощряются. Весовые коэффициенты 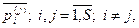 элементы, которых были изменены (поощрены или оштрафованы), нормируется.
элементы, которых были изменены (поощрены или оштрафованы), нормируется.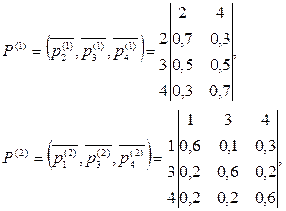
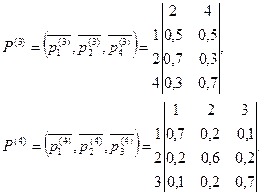
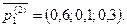 исходящей лс первого выбора является лс к ук № 1. Предположим, что данная лс в настоящий момент времени недоступна. Так как
исходящей лс первого выбора является лс к ук № 1. Предположим, что данная лс в настоящий момент времени недоступна. Так как 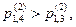 то исходящей лс второго выбора является лс к ук № 4. Допустим, что исходящая лс из ук № 2 к ук № 4 в данный момент времени доступна. Следовательно, данная лс участвует, в организации искомого маршрута. В ук № 4 в соответствии с
то исходящей лс второго выбора является лс к ук № 4. Допустим, что исходящая лс из ук № 2 к ук № 4 в данный момент времени доступна. Следовательно, данная лс участвует, в организации искомого маршрута. В ук № 4 в соответствии с  выбираем исходящую лс к ук № 1. Допустим, она доступна. Следовательно, маршрут между уи и уп
выбираем исходящую лс к ук № 1. Допустим, она доступна. Следовательно, маршрут между уи и уп 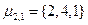 организован. Лс, участвующие в данной процедуре, поощряются. Соответствующие весовые коэффициенты
организован. Лс, участвующие в данной процедуре, поощряются. Соответствующие весовые коэффициенты  увеличиваются (предположим, что на 0,2), а вектора
увеличиваются (предположим, что на 0,2), а вектора  нормируются. В результате получаем новые числовые значения:
нормируются. В результате получаем новые числовые значения: 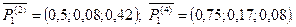
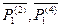 изменятся и примут следующий вид:
изменятся и примут следующий вид: 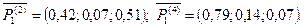 анализируя ситуацию с вектором
анализируя ситуацию с вектором  , видно, что исходящая лс к ук № 4 из ук № 2 при поиске маршрута к ук № 1 приняла значение первого выбора, так как ее весовой коэффициент
, видно, что исходящая лс к ук № 4 из ук № 2 при поиске маршрута к ук № 1 приняла значение первого выбора, так как ее весовой коэффициент 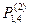 стал максимальным из всех возможных в данном векторе.
стал максимальным из всех возможных в данном векторе.
 как вероятности выбора соответствующих исходящих лс
как вероятности выбора соответствующих исходящих лс 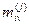 , то можно предположить, что игровой метод решает задачу глобальной оптимизации сети связи по критерию – вероятность установления соединения между парами уи и уп.
, то можно предположить, что игровой метод решает задачу глобальной оптимизации сети связи по критерию – вероятность установления соединения между парами уи и уп.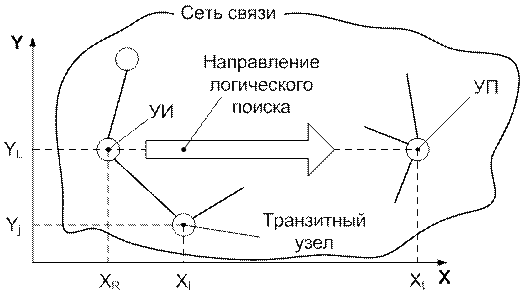
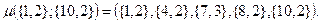 достоинством данного метода является простота и отсутствие необходимости передачи служебной информации по сети. В то же время логический метод не является динамическим и не решает задачу глобальной оптимизации при.
достоинством данного метода является простота и отсутствие необходимости передачи служебной информации по сети. В то же время логический метод не является динамическим и не решает задачу глобальной оптимизации при.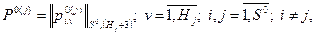 которая имеет следующий вид:
которая имеет следующий вид:


