
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение корректирующих кодов.Содержание книги
Поиск на нашем сайте Каждому символу исходного алфавита сообщений объема na поставим в соответствие n-элементную двоичную последовательность - кодовую комбинацию. Возможное (общее) число последовательностей длины n составляет n0=2n, причем должно соблюдаться условие n0>na. Если n0=na, то все возможные последовательности n-элементного кода используются для передачи или, как говорят, являются разрешенными. Полученный таким образом код называется простым.
1. Для передачи сообщений, число которых равно восьми (na=8), используется трехэлементный код. Число кодовых комбинаций, которое можно при этом получить, n0=23=8. Из таблицы 7.1 видно, что комбинация под номером 0 отличается от комбинации 1 только в одной позиции. Следовательно, если при передаче комбинации 000 произойдет ошибка в третьем элементе, то получим комбинацию 001. Степень различия комбинаций определяется расстоянием хемминга d. Это расстояние для любых двух кодовых комбинаций определяется числом несовпадающих в них разрядов. Например, две ниже написанные друг под другом комбинации не совпадают в двух разрядах:
Поэтому расстояние хемминга d =2. Иначе его определяют как вес суммы по модулю два (
Перебрав все возможные пары кодовых комбинаций, можно найти минимальное хеммингово расстояние, которое принято называть кодовым и обозначать d0. Для примера 6.1 кодовое расстояние d0=1. Рассмотренный в примере код простой. Любая ошибка (даже одиночная!) При использовании такого кода приведет к тому, что переданная разрешённая кодовая комбинация перейдет в другую разрешенную. Таким образом, простой код не способен обнаруживать и тем более исправлять ошибки и имеет d0=1. Для того чтобы код мог обнаруживать ошибки, необходимо, чтобы соблюдалось неравенство na<n0. При этом неиспользуемые n-элементные кодовые комбинации, число которых (n0-na), будем называть запрещенными. Они определяют избыточность кода. Очевидно, что появление ошибки в кодовой комбинации будет обнаружено, если переданная разрешенная комбинация перейдет в одну из запрещенных. В качестве np=na разрешенных кодовых комбинаций надо выбирать такие, которые максимально отличаются друг от друга. 2. Алфавит передаваемых сообщений na=2. Выберем из числа комбинаций, представленных в таблице 6.1, две. Очевидно, что ими должны быть комбинации 000, 111 или 001 и 110 и т.д. Кодовое расстояние d0=3. Ошибки кратности один или два превращают любую разрешенную кодовую комбинацию в запрещенную. Следовательно, максимальная кратность обнаруживаемых таким образом ошибок равна двум (tо.ош=2). Нетрудно догадаться, что минимальное кодовое расстояние d0 и гарантированно обнаруживаемая кратность ошибок связаны соотношением tо.ош=d0-1. Исправление ошибок возможно также только в том случае, если переданная разрешенная кодовая комбинация переходит в запрещенную. Вывод о том, какая кодовая комбинация передавалась, делается на основании сравнения принятой запрещенной комбинации со всеми разрешенными. Принятая комбинация отождествляется с той из разрешенных, на которую она больше всего похожа, т.е. С той, от которой она отличается меньшим числом элементов. Так, если в примере 6.2 при передаче кодовой комбинации 000 получим 001, то вынесем решение, что передавалась кодовая комбинация 000. Связь между d0 и кратностью исправляемых ошибок определяется выражением tи.ош=(d0/2) – 1 для четного d0 и tи.ош =(d0 – 1) / 2 для нечетного d0. Итак, задача получения кода с заданной корректирующей способностью сводится к задаче выбора (путем перебора) из n0=2n кодовых комбинаций na комбинаций с требуемым кодовым расстоянием d0. Если n достаточно мало, то такой перебор не представляет особого труда. При больших n перебор может оказаться непосильным даже для современной эвм, поэтому на практике используют методы построения кодов, не требующие перебора с целью получения кода с заданным d0 и отличающиеся невысокой сложностью реализации.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

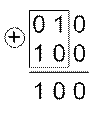
 – условное обозначение суммы) этих кодовых комбинаций. Весом w кодовой комбинации называется число входящих в нее ненулевых элементов.
– условное обозначение суммы) этих кодовых комбинаций. Весом w кодовой комбинации называется число входящих в нее ненулевых элементов.


