
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання мікрокінетики хімічних реакцій.Содержание книги
Поиск на нашем сайте
Пряма й зворотна задача Моделювання мікрокинетіки (у подальшому, для скорочення – кінетики) передбачає розв’язання двох задач: а) пряма задача – побудова кінетичних рівнянь й кривих, виходячи з уявлень про механізм реакції і величин констант швидкості елементарних реакцій; б) зворотна задача – оцінка кінетичних параметрів (констант швидкості, порядків реакцій, енергій активації і предекспонентного множника), виходячи з експериментальних даних. Для побудови кінетичних рівнянь, виходячи з механізму, необхідно використати такий алгоритм: а) підрахувати кількість усіх продуктів – учасників реакції (вхідних, проміжних, вихідних). Їх кількість буде дорівнювати кількості рівнянь кінетики; б) для кожного з продуктів, виходячи зі схеми механізму, виявити шляхи його створення і витрат. Це зручно робити графічно; в) скласти кінетичне рівняння зміни концентрації кожного з реагентів як алгебраїчну суму швидкостей елементарних реакцій створення і витрачення цей речовини за формулою:
г) правила запису рівнянь швидкості елементарної реакції:
1) швидкість накопичення речовини С: - береться зі знаком «плюс»; - дорівнює добутку концентрацій речовин, що створюють С у ступенях, що дорівнюють коефіцієнтам при них; - помножається на коефіцієнт р при продукті С у рівнянні елементарної реакції:
2) швидкість витрати речовини А: - береться зі знаком «мінус»; - дорівнює добутку концентрацій речовин, що створюють С у ступенях, що дорівнюють коефіцієнтам при них; - помножається на коефіцієнт n при продукті A у рівнянні елементарної реакції:
аналогічно укладаються рівняння для інших учасників реакції. г) провести інтегрування системи диференціальних рівнянь, що отримали, користуючись початковими умовами Сі(0) = Сі0, де Сі0 – початкова концентрація і-го учасника реакції, і = 1,…,n (n – загальна кількість учасників реакції). Фізичний сенс цього: початковий склад суміші, що реагує, є відомим. Як правило (але не завжди) початкові концентрації проміжних і кінцевих продуктів дорівнюють нулю. Приклад 14.3 Скласти систему кінетичних рівнянь для схеми перебігу реакцій (14.20) при початкових умовах: СА(0) = 1,1 кмоль/м3; СВ(0) = 1,3 кмоль/м3
Початкові концентрації проміжних і кінцевих продуктів: {СС(0); CD(0); CE(0); CR(0)} = 0
Розв’язання а) Кількість учасників процесів: 6, відповідно, A, B, C, D, E, R. Система повинна містити 6 диференціальних рівнянь; б) укладаємо схему шляхів створення і витрачення кожного з 6 учасників (рис. 14.5); в) у відповідності до схеми (14.12) укладаємо кінетичне рівняння для концентрації речовини А: 1) маршрут створення речовини А: 2C + D = A, швидкість за маршрутом: 2) маршрути витрати речовини А: - на створення С і D: A + B = 2C + D; - на створення Е: 3D+ A = E; - на створення R: 2A = R; Кінетичне рівняння:
Початкові умови: СА(0) = 1,1 кмоль/м3; г) укладаємо кінетичне рівняння для концентрації речовини В: 1) маршрут створення речовини В: 2C + D = В, швидкість за маршрутом: 2) маршрут витрати речовини - на створення С і D: A + B = 2C + D;
Кінетичне рівняння:
Початкова умова: СВ(0) = 1,3; д) укладаємо кінетичне рівняння для концентрації речовини С: 1) маршрут створення речовини С: А + В = 2С + D, швидкість за маршрутом: 2) маршрут витрати речовини С: 2С + D = A + B, швидкість за маршрутом:
е) укладаємо кінетичне рівняння для концентрації речовини D: 1) маршрут створення речовини D: А + В = 2С + D, швидкість за маршрутом: 2) маршрути витрати речовини D: - на перетворення 2С + D = A + B, швидкість за маршрутом: - на перетворення 3D + A = E, швидкість за маршрутом: Кінетичне рівняння:
ж) укладаємо кінетичні рівняння для речовин Е і R. Це – кінцеві продукти, вони тільки створюються, і укладання рівнянь згідно зі схемою (14.20) не викликає проблем:
Метод А.А.Баландіна Для автоматизації і формалізації укладання систем кінетичних рівнянь складних реакцій використовують матричний метод, запропонований видатним радянським фізико-хіміком А.А.Баландіним. Проілюструємо його на прикладі схеми (14.12): а) перепишемо рівняння хімічних реакцій (4.20) у вигляді системи однорідних рівнянь:
Еквівалентна запис – через стехіометричну матрицю:
б) приєднаємо до матриці Х діагональні матриці: 1) зверху – матрицю концентрацій речовин Т 1. На її головної діагоналі розташовані позначення концентрацій усіх речовин, що беруть участь у реакціях, у такому же порядку, що й у стехіометричної матриці, тобто, у нашому випадку:
2) збоку – матрицю констант швидкості Т 2 На її головної діагоналі розташовані константи швидкості усіх реакцій системи, з номерами у відповідності до стехіометричної матриці. У нашому випадку:
б) Як результат отримуємо приєднану матрицю W виду (14.31).
Пусті місця в структурі матриці означають, що там стоять нульові елементиВ неї підматрицю Х можна розглядати, як матрицю орієнтації Т 2 відносно Т 1. Кожній речовині відповідає свій стовпчик у Х, а кожній реакції – свій рядок. У підматриці Х на місцях перетинання стовпця j з підматриці Т 1 і рядку k з підматриці Т 2 можуть знаходитись: - нулі, якщо речовина j не бере участі в реакції k; - стехіометричні коефіцієнти при речовині j в реакції k, якщо вона бере в неї участь; в) можна показати, що для похідних від концентрації по часу є вірним матричне рівняння (14.32):
де К = Х Т× Т 2 – матриця констант швидкості з врахуванням стехіометрії; Мс – матриця-рядок добутків концентрації речовин – вхідних продуктів кожної елементарної реакції, у ступенях, що дорівнюють стехіометричним коефіцієнтам. Її розмір: (1´n), де n – число елементарних реакцій (кількість рядків підматриці Х). Для схеми (4.20) ця матриця має вид:
г) для знаходження і-го елементу матриці Мс можна користуватися такими правилами: 1) в і-тому рядку матриці Х знайти позиції k1,…,kq негативних коефіцієнтів (вони відповідають вхідним речовинам і-тої реакції); 2) на головної діагоналі підматриці Т1 знайти концентрації речовин, що знаходяться у позиціях k1,…,kq. Вони відповідають концентраціям речовин 3) записати вираз для і-го елементу:
де |Xij| - модуль відповідного стехіометричного коефіцієнту – частковий порядок реакції по j-му реагенту. У реальних задачах величини |Xij| складають 1 або 2, а кількість множників – 1 або 2 і дуже рідко 3. Неважко з’ясувати на прикладі схеми (14.20), що метод Баландіна дає такі ж самі результати, як і «прямий» метод, описаний у прикладі 14.3. Але перевага методу Баландіна – в тому, що достатньо лише сформувати, виходячи з механізму реакції, матрицю W, задав числові значення констант швидкості і далі, можна відразу користуватися нею для розв’язування системи диференціальних рівнянь, без попереднього розкриття у символьному виді. Наступний крок у моделювання – це розв’язання системи диференціальних рівнянь кінетики. Як правило, можливим у більшості випадків є тільки числовий розв’язок. При цьому слід розрізняти 2 принципових випадки: коли константи швидкості розрізняються не більше, ніж на 2 порядки, і коли їх розбіжності перевищують 2-3 порядки. У першому випадку маємо нежорстку систему, яку можна успішно розв’язати за допомогою стандартних ефективних явних методів, наприклад, крокових (Рунге-Кути, Булірша-Штоєра) або корекції-прогнозу (Адамса-Башфорта). У другому випадку маємо жорстку систему, для розв’язання якої необхідно використовувати спеціальні так звані неявні методи, наприклад, метод Гіра. Неявні сучасні методи інтегрування жорстких систем диференціальних рівнянь входять до більшості пакетів прикладної математики (MathCAD, MathLab, SciLab), але їх самостійна програмна реалізація, наприклад в разі необхідності укладання програм керування процесами, є складною задачею. Відмітимо, що детальні механізми складних багатостадійних реакцій відомі лише для невеликої кількості процесів. Вивчення механізмів реакцій є дуже складною трудомісткою задачею, що вимагає багато матеріальних ресурсів і тому дуже дорого коштує. Для багатьох практичних задач буває достатньо отримати емпіричну залежність швидкості від концентрації реагентів і температури.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.007 с.) |

 , (14.16)
, (14.16)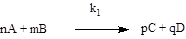 (14.17)
(14.17) (14.18)
(14.18) . (14.19)
. (14.19)
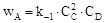 ;
;

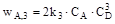
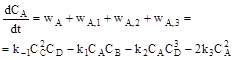 (14.21)
(14.21)

 ; (14.22)
; (14.22) ;
; . Кінетичне рівняння:
. Кінетичне рівняння: ; (14.23)
; (14.23)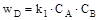


 ; (14.24)
; (14.24) ; (14.25)
; (14.25) . (14.26)
. (14.26)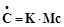 , (14.32)
, (14.32) - вектор-стовпець похідних концентрацій речовин системи;
- вектор-стовпець похідних концентрацій речовин системи;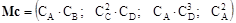 (14.33)
(14.33) , що входять у рівняння швидкості,
, що входять у рівняння швидкості, ; (14.34)
; (14.34)


