
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение уравнения степенной регрессииСодержание книги
Поиск на нашем сайте
Уравнение степенной агрессии имеет вид: где a, b параметры, которые определяются по данным таблицы наблюдений. Таблица наблюдений имеет вид
Прологарифмируем исходное уравнение и в результате получим
Данное уравнение есть не что иное, как уравнение линейной регрессии. Для этого прологарифмируем исходные данные:
Далее необходимо выполнить известные нам вычислительные процедуры по нахождению коэффициентов a и b, используя прологарифмированные исходные данные. В результате получим значения коэффициентов b и a'. Параметр a можно найти по формуле
Двухфакторные и многофакторные уравнения регрессии Линейное двухфакторное уравнение регрессии имеет вид
Оптимизация. Основные понятия. Оптимизация - поиск наилучшего решения с учетом ограничений. Для оптимизации ищется целевая функция. Эта функция конструируется искусственно на основе уравнений, описывающих объект оптимизации. Целевая функция обычно имеет много аргументов: φ=f (х1, х2,..., х n). Чтобы найти оптимальное значение, перебирают значение аргументов хi пошагово до тех пор, пока значение φ станет удовлетворять условиям оптимума. разработаны десятки методов оптимизации: - первый строгий математический метод предложил в 1840г. венгерский математик Коши - метод скорейшего спуска. При формулировании задач оптимизации обычно стараются ее свести к поиску минимума. МСС относится к классу градиентных методов. Градиент - вектор, указывающий на направление максимального возрастания функции. Антиградиент – на убывания функции. Для иллюстрации поиска экстремума в процессе оптимизации функций двух переменных используют линии равного уровня. Если задаться постоянным значением φ и так подбирать значения хi чтобы значение φ было равным заданному значению, то геометрическое место точек φ составит линию равного уровня. МСС - простейший метод оптимизации, пригодный для сложных систем. Работа метода хорошо иллюстрируется с помощью линий равного уровня. Порядок поиска оптимума: - выбирается исходная точка в виде значений параметров целевой функции: φ=f (х1, х2,..., х n). - ищется градиент; - движемся в направлении антиградиента с заданным шагом; - на каждом шаге проверяем выполнение условия движения, текущее значение φ должно быть меньше предыдущего. - если условие движения нарушается, то процесс останавливается, иначе, движение продолжается; - при нарушении условий движения уточняется одномерный минимум и ищется новый градиент; - условие останова: а) значение φ меньше заданного; б) разность значений соседних φ меньше заданной; в) количество шагов превышает допустимое. - если после останова минимума не удовлетворяет требованиям, то либо ищется другая исходная точка и процесс повторяется, либо выбирается другой метод оптимизации.
Одномерный поиск оптимума. метод скорейшего спуска представляет собой многомерный поиск, т.к. минимум ищется на разных направлениях. Когда минимум ищется только в одном направлении для уточнения направления следующего уровня - одномерный поиск. Одномерный поиск Для многомерного поиска разработаны десятки методов, для одного поиска около 1 десятка методов. Рассмотрим одномерное приближение. Метод последовательных приближений (р) P - длина шага оптимизации; φ - значение целевой функции 1. при нарушении условий движения (φi+1 > φi) движение останавливается 2. Возвращается на 1 шаг назад. 3. Делим длину шага на R где R = 3-10 4. Возобновляем движение с новым шагом. 5. При нарушении условий движения все повторяется, и т.д. Условия останова: - Значение j < заданного - Разность между соседними значениями j < заданной - Длина шага < заданной - Кол-во шагов превышает заданное. Любое из этих условий приводит к останову. Метод золотого сечения Если возьмем пропорцию: x1/x = x2/x1 = 0.618-mo (р) Такое соотношение называется золотой пропорцией. 1. При нарушении условий движения последний шаг делим в отношении золотой пропорции слева на право. 2. Этот же отрезок делим в золотой пропорции справа на лево. В результате получим 2 новые точки 3. Сравниваем значения j в новых точках. 4. Выбираем отрезок, которому соответствует меньшее из этих двух j. 5. Полученный отрезок делим в отношении золотой пропорции слева направо, и т.д. Условия останова те же, что и в предыдущем случае. Метод параболической аппроксимации (р) При нарушении условий значения j в последних 3-х точках подставляется в формулу решения системы 3-х уравнений для параболы. Это решение позволяет находить координаты минимума параболы, роходящий через 3 последние точки. Сравнение методов одномерного поиска МПП более прост (движемся, делим), но требует много шагов (м.б. 10 и 100 шагов). МЗС позволяет найти min за 3-4 шага. МПА более сложен, но позволяет найти min за 1 шаг. Но МПА обладает методической погрешностью, поскольку парабола отличается от истинной кривой; обычно эта погрешность невелика. В пакетах программ для расчета оптики обычно используется в качестве метода многомерного поиска демнорированый МСС, а в качестве метода одномерного поиска - МПА.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.105.222 (0.006 с.) |


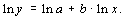 Обозначим lny через y', lna как a', а lnx как x'. В результате подстановки получим
Обозначим lny через y', lna как a', а lnx как x'. В результате подстановки получим 

 где a, b1, b2 параметры; x1, x2 экзогенные переменные; y эндогенная переменная. Степенное двухфакторное уравнение регрессии имеет вид
где a, b1, b2 параметры; x1, x2 экзогенные переменные; y эндогенная переменная. Степенное двухфакторное уравнение регрессии имеет вид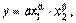 Для нахождения параметров этого уравнения его необходимо прологарифмировать. В результате получим
Для нахождения параметров этого уравнения его необходимо прологарифмировать. В результате получим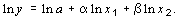 Следует помнить, что мы получим не параметр a, а его логарифм, который следует преобразовать в натуральное число. Линейное многофакторное уравнения регрессии имеет вид
Следует помнить, что мы получим не параметр a, а его логарифм, который следует преобразовать в натуральное число. Линейное многофакторное уравнения регрессии имеет вид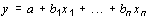 , где a, b1, bn параметры; x1, xn экзогенные переменные; y эндогенная переменная.
, где a, b1, bn параметры; x1, xn экзогенные переменные; y эндогенная переменная.


