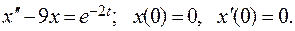Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неопределённый и определённыё интегралыСодержание книги
Поиск на нашем сайте
281-290. Найти неопределенные интегралы. В двух примерах (пункты а и б) проверить результаты дифференцированием. 281. а) в) 282. а) в) 283. а) в) 284. а) в) 285. а) в) 286. а) в) 287. а) в) 288. а) в) 289. а) в) 290. а) в)
301-310. Вычислить несобственный интеграл или доказать его расходимость. 30 1. 30 3. 30 5. 30 7. 30 9.
Дифференциальные уравнения 321-330. Найти общее решение дифференциального уравнения. 321. 323. 325. 327. 329.
341-350. Найти частное решение дифференциального уравнения 341. 342. 343. 344. 345. 346. 347. 348. 349. 350.
Двойные и криволинейные интегралы 351-360. Вычислить двойные интегралы по области D. 351. 352. 353. 354. 355. 356. 357. 358. 359. 360.
361 – 370. Перейдя к полярным координатам, вычислить площадь фигуры, ограниченной областью D. 361. Область D ограниченна линиями: 362. Область D ограниченна линиями: 363. Область D ограниченна линиями: 364. Область D ограниченна линиями: 365. Область D ограниченна лемнискатой: 366. Область D ограниченна линиями: 367. Область D ограниченна линиями: 368. Область D ограниченна линиями: 369. Область D ограниченна линиями: 370. Область D ограниченна лемнискатой:
371 – 380. Вычислить криволинейные интегралы 371. 372. А(2;4). 373.
374. 375. 376.
377. 378. 379. 380. РЯДЫ
421-430. Исследовать сходимость числового ряда. 421. 423. 425. 427. 429. 431-440. Найти область сходимости степенного ряда. 431. 433.
435. 437. 439. 441-450. Вычислить определенный интеграл 441. 443. 445. 447. 449.
451 – 460. Найти три первых отличных от нуля члена разложения в степенной ряд решения 451. 452. 453. 454. 455. 456. 457. 458. 459. 460. 461 – 470. Разложить данную функцию 461. 462. 463. 464. 465. 466.
467.
468.
469. 470. 481 – 490. Представить заданную функцию 481. 482. 483. 484. 485. 486. 487. 488. 489. 490.
Операционное исчисление 501-510. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. 501. 502. 503. 504. 505. 506. 507. 508. 509. 510.
511-520. Методом операционного исчисления найти частное решение системы дифференциального уравнения, удовлетворяющее начальным условиям. 511. 512. 513. 514.
515. 516. 517. 518. 519. 520.
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.83.45 (0.009 с.) |

 ; б)
; б) 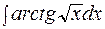 ;
; ; г)
; г) 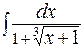 .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г) 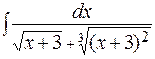 .
. ; б)
; б)  ;
; ; г)
; г) 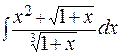 .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
.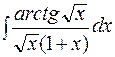 ; б)
; б)  ;
; ; г)
; г) 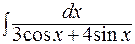 .
. ; б)
; б)  ;
; ; г)
; г)  .
.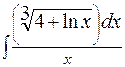 ; б)
; б)  ;
; ; г)
; г)  .
. . 30 2.
. 30 2.  .
. . 30 4.
. 30 4.  .
.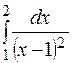 . 306.
. 306. 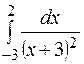 .
.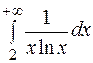 .
.  30 8.
30 8.  .
. . 310.
. 310. 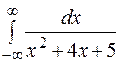 .
. . 322.
. 322.  .
.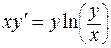 . 324.
. 324.  .
. . 326.
. 326.  .
. . 328.
. 328.  .
. . 330.
. 330.  .
. , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
,  .
. ;
;  ,
,  .
. ;
;  ,
,  .
. ;
;  ;
;  ,
,  ;
;  .
. ;
; 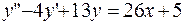 ;
;  ;
;  ,
,  ;
; 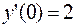 .
. ;
;  ,
, 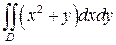 , где D – область, ограниченная линиям
, где D – область, ограниченная линиям 
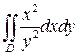 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
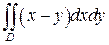 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
 где D – область, ограниченная линиями
где D – область, ограниченная линиями 
 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 
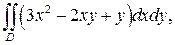 где D – область, ограниченная линиями
где D – область, ограниченная линиями 
 где D – область, ограниченная линиями
где D – область, ограниченная линиями 

 где D – область, ограниченная линиями
где D – область, ограниченная линиями .
. (І четв.)
(І четв.) .(І четв.)
.(І четв.) . (І четв.)
. (І четв.)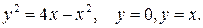
 (І четв.)
(І четв.)




 где L – контур треугольника, образованного осями координат и прямой
где L – контур треугольника, образованного осями координат и прямой  в положительном направлении, т.е. против движения часовой стрелки.
в положительном направлении, т.е. против движения часовой стрелки. где L – дуга параболы
где L – дуга параболы 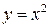 от точки О (0;0) до точки
от точки О (0;0) до точки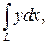 где L – контур прямоугольника, образованного прямыми
где L – контур прямоугольника, образованного прямыми в положительном направлении (против часовой стрелки).
в положительном направлении (против часовой стрелки).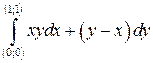 вдоль кривой
вдоль кривой  .
. вдоль кривой
вдоль кривой  вдоль
вдоль  отточки О (0;0) до точки А(1;1).
отточки О (0;0) до точки А(1;1). , где L – четверть окружности
, где L – четверть окружности  0
0  , против часовой стрелки.
, против часовой стрелки. , где L – первая арка циклоиды
, где L – первая арка циклоиды  0
0  .
. вдоль линии
вдоль линии  от точки О (0;0) до точки А(1;1).
от точки О (0;0) до точки А(1;1).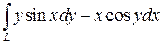 вдоль отрезка ОА, О (0;0),
вдоль отрезка ОА, О (0;0),  .
. . 422.
. 422.  .
. . 424.
. 424.  .
. . 426.
. 426.  .
. . 428.
. 428.  .
. . 430.
. 430.  .
. . 432.
. 432.  .
. . 434.
. 434.  .
. . 436.
. 436.  .
. . 438.
. 438.  .
. . 440.
. 440.  .
. с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.
с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно. . 442.
. 442.  .
.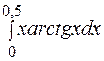 . 444.
. 444.  .
. . 446.
. 446.  .
. . 448.
. 448.  .
. . 450.
. 450.  .
. дифференциального уравнения
дифференциального уравнения  , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  .
.









 в ряд Фурье в интервале
в ряд Фурье в интервале  .
. в интервале
в интервале 
 в интервале
в интервале 
 в интервале
в интервале  в интервале
в интервале 
 в интервале
в интервале  в интервале
в интервале  в интервале
в интервале  в интервале
в интервале  в интервале
в интервале 
 , где
, где  в виде
в виде  проверить, является ли она аналитической. Если да, то найти значение её производной в заданной точке
проверить, является ли она аналитической. Если да, то найти значение её производной в заданной точке  .
.