Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многокритериальные задачи оптимизации в экономике. Формирование целевой функции, стратегии оптимизации.Содержание книги
Поиск на нашем сайте
В многокритериальных задачах критерии векторны. Оценка результатов поиска по изменению множества критериев неоднозначна и противоречива, поэтому непосредственно использовать критерии в алгоритме оптимизации невозможно. Для решения многокритериальной задачи необходимо построить целевую функцию, которая обеспечит обобщенную оценку качества объекта, отображаемую векторным критерием. Процесс построения скалярной функции при многокритериальной оптимизации называется сверткой векторных критериев. Различают следующие виды стратегии: 1 Стратегия частного критерия – в качестве целевой функции принимают один из критериев оптимальности, характеризующий главное его качество. Для остальных критериев используется другая оценка и их используют для назначения ограничений. Формулировка:
где yk – один из выходных параметров, принятый в качестве частного критерия, n – количество внутренних параметров, m – количество выходных параметров 2 Аддитивная стратегия – разделим все выходные параметры на 3 группы: значение которых нужно увеличить (yj+), уменьшить (yk-) или оставить на некотором уровне (yl = Tl+-Δy). Введем вектор весовых коэффициентов С={С1,С2,…,Сm}, характеризующих значимость выходных параметров и вектор нормирующих коэффициентов Y0={y01,…,у0m} и сформируем целевую функцию (ЦФ -> min)
Недостаток стратегии в том, что улучшение целевой функции возможно при ухудшении одного из конфликтных критериев и одновременном улучшении других критериев 3 Мультипликативная стратегия - Мультипликативная стратегия может применяться в тех случаях, когда отсутствуют условия типа равенства и выходные параметры не могут принимать нулевые значения. Целевая функция подлежит максимизации:
Мультипликативная целевая функция имеет тот же недостаток, что и аддитивная, т.е. улучшение одних критериев оптимальности достигается за счёт ухудшение других, коэффициенты Cj могут применяться в качестве степеней. Целевая функция более чувствительная, чем аддитивная. 4 Максиминная стратегия – нацелена на максимальное удовлетворение требований, предъявляемых к объекту. В ее основе лежит идея равномерности, суть которой состоит в выравнивании всех нормируемых критериев оптимальности. Введем количественные оценки степени выполнения требований:
где Tj – значение требования к соответствующему параметру,
Эту функцию называют функцией минимума, а т.к. требуется ее максимизировать, то стратегию называют максиминной max min Sj(x). Для учета значимости вводят коэффициенты штрафа bj. Максиминная стратегия решения многокритериальных задач лишена недостатков ранее рассмотренных моделей. При ее использовании влияние на целевую функцию оказывает лишь тот критерий, который в данной точке пространства управляемых параметров является наихудшим с позиции выполнения требований к объекту. В результате происходит выравнивание оценок степени выполнения по всем критериям Планирование вычислительного эксперимента. Полный факторный эксперимент. При построении экспериментальной факторной модели объект моделирования представляется «черным» ящиком, на вход подаются переменные X,Z, а на выходе регистрируются переменные Y. X- внутренние параметры, Z – внешние параметры, Y – выходные параметры. В вычислительных экспериментах объектом исследования является теоретическая или имитационная модель, на основе которой необходимо установить факторную модель. Эксперимент – система операций, воздействий и наблюдений, направленных на получение информации об объекте при исследовании. Активным называется эксперимент, в котором значения факторов задаются и поддерживаются неизменными в течение опыта в соответствии с планом эксперимента. Основные принципы планирования эксперимента: 1 цель планирования эксперимента – получение максимума информации о свойствах исследуемого объекта при минимуме опыта. Это обусловлено высокой стоимостью экспериментов и вместе с тем – построением адекватной модели 2 в вычислительном эксперименте, в отличие от физического, нет ограничений на выбор управляемых параметров и пределов их изменения. При планировании активных экспериментов применяются принципы 1 отказ от полного перебора всех возможных состояний объект 2 постепенное усложнение структуры матмодели 3 сопоставление результатов эксперимента с величиной случайных помех 4 рандомизация опытов 5 оптимальное планирование эксперимента.
При проведении активного эксперимента задается определенный план варьирования факторов. План эксперимента – совокупность данных, определяющих число, условие и порядок реализации опытов. Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям. Точка плана – совокупность численных значений факторов, соответствующих условиям проведения опыта, т.е. точка факторного пространства, в которой эксперимент, т.е. Xi={X1,X2,…,Xn}. Общая совокупность таких векторов образует план эксперимента. Совокупность различных векторов, число которых n, образуют спектр плана. Матрица плана представляет прямоугольную таблицу, содержащую информацию о количестве и условиях проведения опытов. Строки соответствуют опытам, столбцы – факторам. Матрица спектра плана – матрица, в которую входят только различающиеся между собой строки. План называют насыщенным, если общее число точек плана равно числу неизвестных параметров регрессионной модели. Такой план позволяет получить экспериментальную факторную модель при минимальных затратах. План полного факторного эксперимента. Спектр плана содержит все возможные комбинации значений факторов на всех уровнях изменений. Число точек спектра плана N=Un, где U- число уровней, n – количество факторов. Для составления матрицы спектра плана используется правило: в 1-й строке все факторы = -1, и в 1-м столбце знаки единиц меняются поочередно, во 2-м чередуются через 2, в 3-м – через 4, в 4-м – через 8 и т.д. по степеням двойки.
X=
Т.к. при использовании всех возможных сочетании факторов в уравнении регрессии число определенных коэффициентов Nв = числу точек спектра плана, то такой план – насыщенный. 15. Дробный факторный эксперимент (ДФЭ). Проверка пригодности спектра плана для проведения эксперемента. Наряду с положительными качествами полного факторного эксперимента, он имеет недостаток. Увеличение количества факторов приводит к быстрому росту числа опытов и, что обусловлено степенной зависимостью (2n). Кроме того, необходимо дублирование опытов. Структура регрессионной модели выбирается на основе априорной информации о физических свойствах объекта. Сложно представить влияние на характеристики объекта сочетания факторов выше 2 или 3 порядка. Поэтому часто ограничиваются сочетаниями факторов 2-го порядка и отдельными сочетаниями 3-го порядка. В этом случае полный факторный эксперимент оказывается избыточным. Но тогда должно соблюдаться условие возможности оценки коэффициентов регрессии по результатам опытов, которые выражаются N≥Nв (N-число экспериментов, Nв – число переменных). Во многих случаях описания модели сложной системы в связи с отсутствием необходимой информации о влиянии фактора на выходные параметры строят линейную модель. Так для 3-х факторов Nв=4, а при Nв=3, спектр плана должен иметь 8 точек => 4 опыта оказываются избыточными и их можно сократить на основе принятых условностей. При построении матмодели использующих упрощенное представление регрессии применяют дробные факторные эксперименты. Наибольшее распространение получили планы дробного факторного эксперимента типа 2n-p, p – степень дробности, n – число факторов. Планы ДФЭ принято называть репликами с указанием степени дробности. ДФЭ 2n-1 – полуреплика, ДФЭ 2n-2 – четвертьреплика. Число точек спектра этого плана N=2n-p. При соблюдении такого плана должно соблюдаться условие отсутствия в матрице базисных функций совпадающих или полностью противоположных столбцов. Процедура построения спектра плана ДФЭ:
1 выбор структуры уравнения регрессии и определение степени дробности. Исходят из условия N>Nв 2 выбор ведущих факторов и построение для них матрицы спектра плана. Число ведущих факторов К принимают равным разности между количеством опытов и степенью дробности. Для выбранных К факторов строят план полного факторного эксперимента, используя правило чередования знаков 3 построение матрицы спектра плана ДФЭ. Для этого используется матрица, полученная на 2-м шаге в качестве 1-й части, во 2-ю часть должны войти столбцы матрицы для остальных факторов, число которых равно p. Столбцы матрицы, соответствующие эти факторам определяют путем умножения соответствующих столбцов ведущих факторов. Для этого используют т.н. генерирующее соотношение – алгебраическое выражение, устанавливающее связь между одним из факторов и произведением какой-либо комбинации ведущих факторов. Чтобы полученные столбцы были ортогональными, для каждого из них задается отдельное генерирующее соотношение. Выбор их произволен, но нельзя использовать те произведения ведущих факторов, которые входят в состав существующих переменных, т.к. в этом случае в матрице базисных функций окажутся совпадающие столбцы. Количество ведущих факторов, входящих в генерирующее соотношение может быть произвольным 4 проверка пригодности полученного спектра плана. Для этого необходимо построить матрицу базисных функций и проверить, нет ли совпадающих или противоположных столбцов. Если их нет, то спектр плана пригоден для решения поставленной задачи.
Иначе последовательно выполняется следующая процедура: 1 выбираются иные генерирующие соотношения 2 изменяется набор ведущих факторов 3 уменьшается степень дробности плана р. При ограниченных возможностях проведения опытов, р сохраняю, но изменяют структуру регрессионной модели.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.195 (0.01 с.) |


 ;
; 
 .
.
 - интервал изменения j-го критерия. При таком подходе условия работоспособности должны быть приведены к условию
- интервал изменения j-го критерия. При таком подходе условия работоспособности должны быть приведены к условию 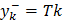 . Значение Sj в этом случае подлежит максимизации, причем в первую очередь те, которые оказываются наименьшими. Целевая функция:
. Значение Sj в этом случае подлежит максимизации, причем в первую очередь те, которые оказываются наименьшими. Целевая функция: