
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие двойственности в задачах линейного программирования (ЗЛП). Правила построения двойственных задач (симметричных и несимметричных).Содержание книги
Поиск на нашем сайте С каждой ЗЛП тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется прямой или исходной. Многие ЗЛП первоначально ставятся в виде исходных или двойственных задач, поэтому говорят о паре взаимно двойственных ЗЛП. Пара симметричных двойственных ЗЛП имеет следующий вид:
Рассмотренная пара взаимно двойственных задач может быть экономически интерпретирована, например, так. Прямая задача: сколько и какой продукции хj (j=1,n) надо произвести, чтобы при заданных стоимостях единицы продукции cj (j=1,n), объемах имеющихся ресурсов bi (i=1,m) и нормах расходов aij максимизировать выпуск продукции в стоимостном выражении? Двойственная задача: какова должна быть оценка единицы каждого из ресурсов yi (i=1,m), чтобы при заданных bi, cj и aij минимизировать общую оценку затрат на все ресурсы. Правила построения симметричных двойственных задач: 1) Если прямая на max, то двойственная к ней на min и наоборот. 2) Коэф-ты целевой ф-ии прямой задачи явл. свободными членами двойственной. 3) Свободные члены bi ограничения прямой задачи явл. коэф-ми целевой функции двойственной задачи. 4) Матрицы коэффициентов прямой и двойственной задач явл. транспонированными друг к другу. 5) Если прямая задача на max то ее сист. ограничений представляется в виде неравенств со знаком <=. Двойственная задача решаемая на min и её сист. ограничений имеет вид неравенств со знаком >=. 6) Число ограничений прямой задачи = числу переменных двойственной, а число ограничений двойственной = числу переменных прямой. 7) Все переменные в задачах неотрицательны. Если среди ограничений прямой задачи имеется равенство или на некоторые переменные не накладывается условие не отрицательности, то построив двойственную линейную задачу, получим пару несимметричных задач. Правила построения несимметричных двойственных задач: 1) Если на переменную xj прямой задачи накладывается условие неотрицательности, то j-ое условие системы ограничений двойственной задачи явл. неравенство. 2) Если на xj прям. задачи не накладывается условие неотрицательности, то j-ое ограничение системы двойственной задачи записывается в виде строгого равенства. 3) Если в прямой задаче имеются ограничения равенства то на соотв. переменные двойственной задачи не накладываются условие неотрицательности. 4. Применение аппарата производственных функций. Свойства и основные характеристики производственных функций. Основными производственными ресурсами являются труд (L) и капитал (K). Математически существующие технологии выражаются через производственную функцию. Если обозначить объем выпускаемой продукции через Y, то ПФ можно записать Y = f (K, L). Это выражение означает, что объем выпуска является функцией количества капитала и количества труда. Производственная функция описывает множество существующих в данный момент технологий. Если изобретается лучшая технология, то при тех же затратах труда и капитала объем выпуска увеличивается. Основным исходным понятием в описании экономического объекта становится технологический способ, который представляется обычно как вектор v затратвыпуска, включающий в себя перечисление объемов затрачиваемых ресурсов (вектор x) и сведения о результатах их преобразования в конечные продукты или другие характеристики (прибыль, рентабельность и т.п.) (вектор y): v = (x; y). Совокупность векторов технологических способов, которые могут служить описанием (с допустимой точки зрения исследователя точностью) производственного процесса, реально осуществимого на некотором объекте, называется технологическим множеством V данного объекта. Для определенности мы будем полагать, что размерность вектора затрат x равна N, а вектора выпуска y соответственно M. Таким образом, технологический способ v является вектором размерности (M + N), а технологическое множество Скажем, что вектор и при этом имеет место по крайней мере одно из двух: а) существует такой номер i 0 , что б) существует такой номер j 0 , что Эффективными считаются те способы, которые не могут быть улучшены ни по одной затратной компоненте, ни по одной позиции выпускаемой продукции, без того чтобы не перестать быть допустимыми. С помощью понятия эффективного технологического множества ПФ можно определить как отображение y = f (x), где Указанное отображение, вообще говоря, является многозначным, т.е. множество f (x) содержит более чем одну точку. В наиболее простом случае ПФ есть скалярная функция N аргументов: Приведенное соотношение описывает границу технологического множества V,поскольку при данном векторе затрат (x 1 ,..., x N ) производить продукции, в количестве большем, чем y, невозможно, а производство продукции в количестве меньшем, чем указанное, соответствует неэффективному технологическому способу. Среди типов производственных функций наиболее часто применяются линейные функции вида Дифференциал
Предельным продуктом переменного ресурса называют прирост общего продукта в связи с увеличением применения данного переменного ресурса на единицу. Предельный продукт труда можно записать как разность MPL = F (K, L + 1) - F (K, L), где MPL предельный продукт труда. Предельный продукт капитала можно также записать как разность MPK = F (K + 1, L) - F (K, L), где MPK предельный продукт капитала. Характеристикой производственного объекта является также величина средней ресурсоотдачи (продуктивности производственного фактора) Частное от деления дифференциальной продуктивности на среднюю Если E j > 1, то величина приростной (дифференциальной) продуктивности превосходит среднюю продуктивность. Таким образом, дополнительная единица ресурса увеличивает не только объем выпускаемой продукции, но и среднюю характеристику ресурсоотдачи
Балансовый метод решения экономических задач. Схема межотраслевого баланса (МОБ). Однопродуктовая модель производства и распределения общественного продукта на уровне всего народного хозяйства (НХ) позволяет увязать основные макроэкономические показатели, такие как валовый продукт, конечный продукт, капвложения, трудовые ресурсы, потребление и другие. Но для эффективного управления экономикой необходимо установить пропорции не только на НХ уровне, но и отраслевом. Это позволяет сделать метод МОБ. Он служит базой определения сбалансированной системы основных показателей. Он представляет кругооборот общественного продукта в целом по НХ и на межотраслевом уровне. Идея МОБ: каждый производимый в НХ продукт должен быть рассмотрен по элементам стоимости как суммы затрат различных продуктов, расходуемых на его изготовление, амортизацию основных фондов, величину зарплаты работников, величину чистого дохода. МОБ может разрабатываться в стоимостном, натуральном и натурально-стоимостном выражении. Наряду с НХ, разрабатывают региональные МОБ по экономическим регионам. Принцип МОБ используется в для построения внутриотраслевых продуктовых балансов, характеризующих связи МОБ с видами производства внутри крупных отраслей. Эти же принципы можно положить в основу баланса предприятия. В МОБ понятие отрасли отличается от общепринятого. В МОБ выделяют «чистые» отрасли – совокупность производств, выпускающих однородную продукцию. Под номенклатурой понимается перечень отраслей, которые вводятся в таблицу МОБ. Схема МОБ производства и распределения совокупного общественного продукта в стоимостном выражении:
В основу этой схемы положено разделение совокупного общественного труда на промежуточный и конечный продукт. 1 квадрант – шахматная таблица межотраслевых связей 2 квадрант – конечная продукция всех отраслей материального производства 3 квадрант – характеризует национальный доход, но со стороны его стоимостного состава как сумма чистой продукции и амортизации 4 квадрант – находится на пересечении 2 и 3 квадрантов, он отражает конечное потребление и использование национального дохода. Метод МОБ применяется для анализа важнейших показателей как труд, фонды, цены и др. В число важнейших входит определение прямых и полных затрат труда на единицу продукции. Обозначим затраты живого труда в производстве j-го продукта как Lj, а объем производства Xj. Тогда прямые затраты труда на единицу Xj:
Полные затраты труда можно представить как сумма прямых затрат и затрат овеществленного труда. Если обозначить полные затраты на единицу j-й продукции через Tj, то произведение aij*tj отражает затраты овеществленного труда, перенесенные на единицу j-го продукта через i-е средство производства. Тогда Тj на единицу (коэффициент полной трудоемкости):
Просуммировав затраты труда по отраслям
Это соотношение – основное балансовое равенство в теории МОБ труда. Сопоставляя потребительский эффект взаимозаменяемой продукции с полными затратами труда на их выпуск можно судить о сравнительной эффективности их производства. Для проверки выполнимости плана по труду на основе отчетного баланса: 1 – t0j (отчетный год) 2 - 3 – L<LП => план не выполним и его следует корректировать. Развитие основной модели МОБ может быть осуществлено путем включения в нее фондоемкости продукции. В этом случае модель дополняется отдельной строкой, в которой указывается в стоимостном выражении объем производственных фондов, занятых в каждой отрасли, где Фj – объемы производственных фондов j-й отрасли, f – коэффициент прямой фондоемкости (он показывает величину производственных фондов непосредственно занятых в производстве данной отрасли в расчете на единицу продукции. Коэффициент полной фондоемкости Fj отражает объем производственных фондов, необходимых во всех отраслях для выпуска j-й продукции.
Можно проверить план: 1- 2 -
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

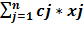
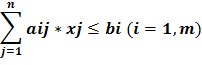
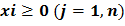
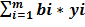
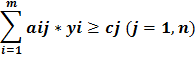
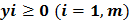
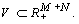
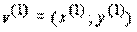 предпочтительнее, чем вектор
предпочтительнее, чем вектор 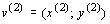 с обозначением
с обозначением 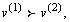 если выполняются следующие условия: 1)
если выполняются следующие условия: 1) 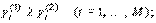 2)
2) 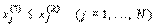
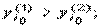
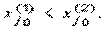
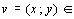 V*.
V*.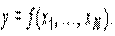
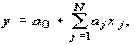 поскольку для них легко решается задача оценивания коэффициентов по статистическим данным, а также степенные функции
поскольку для них легко решается задача оценивания коэффициентов по статистическим данным, а также степенные функции 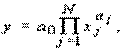 для которых задача нахождения параметров сводится к оцениванию линейной формы путем перехода к логарифмам.
для которых задача нахождения параметров сводится к оцениванию линейной формы путем перехода к логарифмам.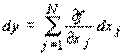 представляет собой изменение стоимости выпускаемой продукции при переходе от затрат набора ресурсов x = (x 1 ,..., x N ) к набору x + dx = (x 1 + dx 1 ,..., x N + dx N ) при условии сохранения свойства эффективности соответствующих технологических способов. Тогда величину частной производной
представляет собой изменение стоимости выпускаемой продукции при переходе от затрат набора ресурсов x = (x 1 ,..., x N ) к набору x + dx = (x 1 + dx 1 ,..., x N + dx N ) при условии сохранения свойства эффективности соответствующих технологических способов. Тогда величину частной производной  можно трактовать как предельную (дифференциальную) ресурсоотдачу или, иными словами, коэффициент предельной продуктивности, который показывает, на сколько увеличится выпуск продукции в связи с увеличением затрат ресурса с номером j на малую единицу. Ожидаемый прирост продукции составит
можно трактовать как предельную (дифференциальную) ресурсоотдачу или, иными словами, коэффициент предельной продуктивности, который показывает, на сколько увеличится выпуск продукции в связи с увеличением затрат ресурса с номером j на малую единицу. Ожидаемый прирост продукции составит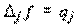 и, следовательно, соотношение
и, следовательно, соотношение 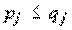 позволит получить дополнительную прибыль.
позволит получить дополнительную прибыль.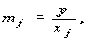 имеющего ясный экономический смысл количества выпускаемой продукции в расчете на единицу используемого ресурса (производственного фактора). Величина, обратная к ресурсоотдаче
имеющего ясный экономический смысл количества выпускаемой продукции в расчете на единицу используемого ресурса (производственного фактора). Величина, обратная к ресурсоотдаче 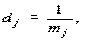 обычно называется ресурсоемкостью, поскольку она выражает количество ресурса j, необходимое для производства одной единицы продукции в стоимостном выражении.
обычно называется ресурсоемкостью, поскольку она выражает количество ресурса j, необходимое для производства одной единицы продукции в стоимостном выражении.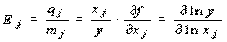 называется коэффициентом эластичности продукции по производственному фактору j и дает выражение относительного прироста продукции (в процентах) при относительном приросте затрат фактора на 1%.
называется коэффициентом эластичности продукции по производственному фактору j и дает выражение относительного прироста продукции (в процентах) при относительном приросте затрат фактора на 1%.
 Конечный продукт
Конечный продукт
 1
1
 Амортизация
Амортизация

 M1
M1





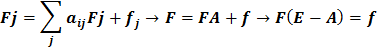

 , если F<Fп => план не выполним.
, если F<Fп => план не выполним.


