Метод исключения в задачах оценивания площади плоских фигур.

По методу монте-карло, у нас есть прямоугольник, в нем есть фигура(кольцо), есть точки которые находятся в этом прямоугольнике, считаем сколько точек попало в круг, и далее по формуле: S(кольца)=(кол-во точек которые попали в кольцо/ общее кол-во)*S(прямоуг)

38. Бутстреп-метод и задача моделирования съема данных с объекта.

39. Генераторы непрерывных одномерных распределений.

40. Этапы компьютерного моделирования (КМ).

41. Проблемы КМ бизнес-процессов.

42. Роль информации в КМ.

Компьютерное моделирование — основа представления знаний в ЭВМ. Компьютерное моделирование для рождения новой информации использует любую информацию, которую можно актуализировать с помощью ЭВМ. Прогресс моделирования связан с разработкой систем компьютерного моделирования, а прогресс в информационной технологии — с актуализацией опыта моделирования на компьютере, с созданием банков моделей, методов и программных систем, позволяющих собирать новые модели из моделей банка.

43. Моделирование бизнес-процессов.

Бизнес-моделирование (деловое моделирование) — деятельность по формированию моделей организаций, включающая описание деловых объектов (подразделений, должностей, ресурсов, ролей, процессов, операций, информационных систем, носителей информации и т. д.) и указание связей между ними. Требования к формируемым моделям и их соответствующее содержание определяются целями моделирования.

Моделирование бизнес-процессов играет огромную роль в управлении бизнес-процессами. Необходимо отметить, что в английском переводе оба вида деятельности имеют одинаковую аббревиатуру BPM (Business Process Modeling и Business Process Management, соответственно), что часто приводит к путанице. Данный факт необходимо учитывать, так как большинство литературы по данному предмету издано на английском языке. Графическое описание бизнес-процессов и их имитация это методы анализа бизнес-процессов, эффективность которых доказана многолетней практикой использования и многочисленными исследованиями. Для графического представления бизнес-процессов используются различные языки, но наиболее популярными и подходящими считаются UML и Business Process Modeling Notation. Моделирование и имитация бизнес процессов являются ключевыми методами для реинжиниринга бизнес-процессов (Business Process Reengineering) и использования методологий непрерывного улучшения бизнес-процессов, например, такими как Six-Sigma.

Информация с ru.wikipedia.org

44. Классификация методов КМ на ЭВМ.

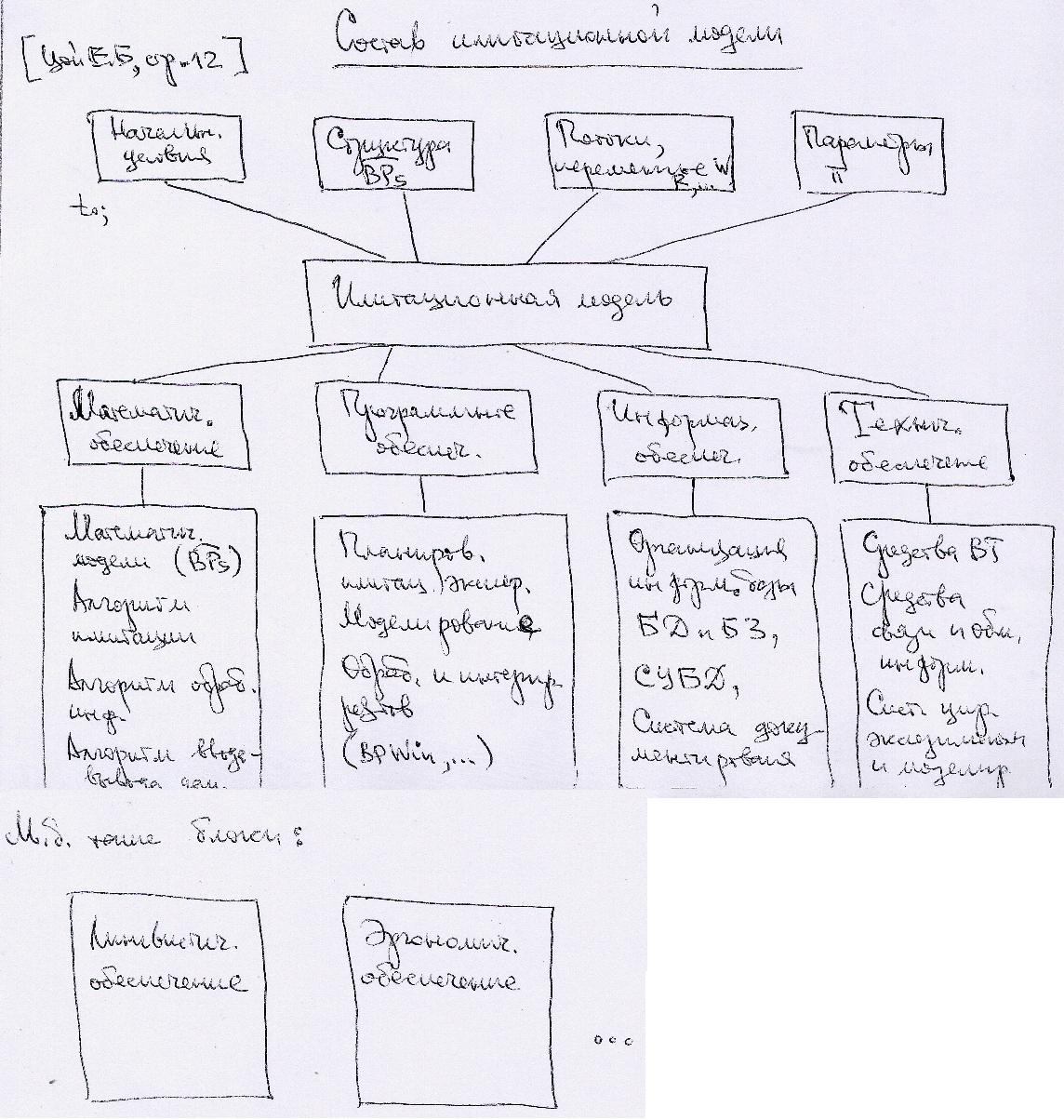
45. Состав имитационной модели.

46. Эффективность КМ и бутстреп-метода.

47. Классификация систем.

48. Датчики псевдослучайных чисел (ДПСЧ) (физические, программные,…).

49. Оценивание качества ДПСЧ.

50. Моделирование дискретных случайных величин.

51. Моделирование непрерывных случайных величин.

Во многих программных средах имеются генераторы случайных (псевдослучайных) чисел, которые обеспечивают формирование случайных чисел, равномерно распределенных в интервале . На основе этого распределения могут быть сформированы выборки случайных чисел с каким-либо другим законом распределения случайной величины. В некоторых случаях этого можно добиться на основе метода инверсии, или метода обратной функции. Суть метода обратной функции заключается в следующем.

Метод обратной функции нельзя применять напрямую к непрерывным распределениям, для которых функция распределения не может быть выражена в квадратурах от соответствующей функции плотности. Типичными примерами такого рода являются нормальное распределение, гамма-распределение, логарифмически-нормальное распределение, а также дискретное распределение Пуассона. В таких случаях для получения выборок случайных чисел можно воспользоваться одним из следующих методов:

1. аппроксимацией непрерывной функции дискретной функцией распределения;

2. получением с помощью статистических соотношений необходимой информации на основе других распределений, имеющих простую аналитическую форму.

Например, в случае второго метода, случайная величина, подчиняющаяся распределению Эрланга -го порядка (или гамма-распределению с целочисленным параметром), представляет собой сумму экспоненциально распределенных случайных величин, а время между наступлениями событий в пуассоновском процессе также распределено экспоненциально.

52. Совместное использование КМ и бутстреп-метода.

53. Прикладные аспекты КМ (вычисление интегралов, объемов, координат центров тяжести плоских фигур и др.).

54. Применение метода исключения в задачах КМ.

55. Блок-схема алгоритма бутстреп-метода.

56. Блок-схема алгоритма вычисления интеграла методом исключения.

57. Блок-схема алгоритма работы датчика непрерывного равномерного распределения.

58. Блок-схема алгоритма работы датчика равномерного дискретного распределения.

 

 

Для начала рассмотрим случай, когда все исходы дискретного распределения имеют одну и ту же вероятность. Если число исходов равно n, то эта вероятность равна, очевидно, 1 / n.

Разделим отрезок [0, 1] на n равных частей, перенумерованных от 0 до n − 1: I ₀, I ₁,..., I_{n − 1}. Далее рассматривается равномерно распределенная случайная величина ξ и функция от нее η = h (ξ) = floor(ξ × n), паскалевская процедура floor(x)вычисляет наибольшее целое число, не превосходящее x.

Легко видеть, что случайная величина η принимает значения от 0 до n − 1 и вероятность наступления каждого исхода одна и та же.

Вот график, показывающий результаты 100 наблюдений этой случайной величины с датчиком случайных чисел системы Excel. Мы видим, что наблюдаемые частоты (голубые столбики, снизу написаны соответствующие им частоты и значения случайной величины) довольно сильно отличаются от теоретически ожидаемых значений (лиловые столбики).

При увеличении числа экспериментов точность, вообще говоря, повысится. Посмотрим, что получилось, когда мы довели число наблюдений до 400.

 

Как видите, у одного из значений получилось такое же значительное относительное (т. е. долевое) отклонение, а, значит, в абсолютных величинах оно увеличилось в четыре раза.

59. Блок-схема алгоритма проверки качества датчика непрерывного равномерного распределения.

60. Блок-схема алгоритма работы датчика двумерного равномерного непрерывного распределения на круге.

начало

r, N, x0,y0

a=x0-r b=y0+r c=y0-r d=y0+r

i=1

x=rand*(b-a)+a y=rand*(d-c)+c

l=

l≤r

+

xi=x yi=y

i=i+1

i≤N

+

61. Блок-схема алгоритма работы датчика одномерного равномерного дискретного распределения на множестве студентов группы (для составления графика дежурств).

N=20; A[N]=…; i=1

R=A[i]

I =I + 1

I < N

Вывод R

62. Блок-схема алгоритма работы датчика двумерного равномерного дискретного распределения на множестве студентов 2-х группы (для выбора пар дежурных).

N=20; M=23; A[N]=…; B[M]=…; i=1; j=1

R1=A[i]

I =I + 1

I < N

R2=B[j]

J < M

j =j + 1

Rez = (R1; R2)

63. Блок-схема алгоритма работы датчика двумерного равномерного непрерывного распределения на квадрате.

64. Блок-схема алгоритма работы датчика дискретного распределения.

 

M = α; i=1

M=M-p(i)

M>=0

ξ=x(i)

i=i+1

65. Блок-схема алгоритма работы датчика одномерного непрерывного распределения с использованием обратного преобразования.

66. Блок-схема алгоритма работы датчика одномерного непрерывного распределения с использованием кусочно-постоянной аппроксимации.

67. Блок-схема алгоритма работы датчика одномерного непрерывного распределения с использованием кусочно-линейной аппроксимации.

68. Блок-схема алгоритма работы датчика одномерного непрерывного распределения с использованием метода исключения.

69. Блок-схема алгоритма работы датчика равномерного распределения,

.

x

x(1)=0; a=2; c=0,1; m=20; i=1

X(i+1) = a * x(1) + c

X(i+1) > m

i=i+1

end

70. Блок-схема алгоритма работы датчика двумерного равномерного непрерывного распределения на круге.

71. Блок-схема алгоритма работы датчика двумерного равномерного дискретного распределения на кольце.

ВЕРА

АРТЕМ

ГРЕГ

ТАНЯ