Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Р е ш е н и е. Здесь нужно решать смешанную задачуСодержание книги
Поиск на нашем сайте
методом разделения переменных, полагая u (x, t)= X (x) T (t). Тогда
Собственные значения и собственные функции определяются из задачи
поэтому на этот раз смешанная задача решается рядом с неопределенны-
ми коэффициентами:
Подставляя этот ряд в начальное условие, будем иметь
и следовательно окончательный ответ будет иметь вид
194. Дан однородный шар радиуса b, центр которого расположен в начале координат. Внешняя поверхность шара поддерживается при нулевой температуре, а начальная температура лите температуру u (r,t) внутри шара при t >0. Р е ш е н и е. Поставленная задача равносильна смешанной задаче
Следуя схеме метода Фурье, полагаем u (r,t) =R (r) T (t)и после подстанов-ки в уравнение получим
Из граничных условий будем иметь
Следовательно, нужно решать задачу Штурма
При решении уравнения
и тогда пишем ряд с неопределенными коэффициентами
В силу начального условия будем иметь
и стало быть ответ в задаче имеет вид
195. Найдите распределение температуры в однородном шаре радиуса b, внутри которого при t ³0 действует источник тепла с постоянной плот- ностью q, а его поверхность поддерживается при нулевой температуре. Начальная температура во внутренних точках шара равна нулю. Р е ш е н и е. Здесь нужно иметь дело со смешанной задачей:
Функция
относительно новой функции v (r,t) придем к смешанной задаче
которая несущественно отличается от задачи 194. В итоге окончательно получим ответ:
196. Найдите решение смешанной задачи
Р е ш е н и е. Непосредственно проверяется, что функция w=t (x+ 1) удовлетворяет уравнению и граничным условиям
поэтому после замены u (x,t) =v (x,t) + t (x+ 1) относительно новой функции v (x,t) получим смешанную задачу
решение которой находится в виде ряда по собственным функциям зада- чи Штурма
Подставляя ряд
К полученным дифференциальным уравнениям для функций нужно присоединить условие
откуда находим
где 197. Сфера радиуса b содержит растворенное вещество с начальной концентрацией u 0. Концентрация на поверхности сферы поддерживается постоянной, равной u 1 >u 0. Найдите количество абсорбированного вещества в момент времени t >0. 198. Решите задачу об остывании однородного стержня длиной l с тепло- изолированной боковой поверхностью, если его начальная температура u (x, 0) =l-x, концевая точка x= 0 теплоизолирована, а x=l поддерживается при постоянной температуре. 199. Дан тонкий однородный стержень длиной l, начальная температура которого равна нулю. На конце x=l поддерживается нулевая темпера- тура, а на конце x= 0 температура растет линейно со временем, так что u (0 ,t) =At, где A – константа. Найдите распределение температуры u (x,t) при t >0. Решите следующие смешанные задачи
201. 202. 203. 204. 205. 206.
224. 225.
§ 7. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ И РЕШЕНИЕ СМЕШАННЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО И ПАРАБОЛИЧЕСКОГО ТИПОВ Дифференциальное уравнение 2-го порядка
принято называть уравнением Бесселя порядка v или уравнением цилин- дрических функций. Здесь Если
где
Если v=n, n= 0,1,2,…, то функция Jn (x) и J-n (x) линейно зависимы, что можно установить посредством соотношений (67),(68). В этих обстоят- ельствах для представления общего решения употребляются цилиндриче- ские функции Вебера-Неймана:
Функция Nn (x) линейно независима от Jn (x), для нее имеется представ- ление в виде ряда
из которого видно, что функция Вебера-Неймана не ограничена в окрест- ности точки х= 0. Вместо соотношения (66) при v=n общее решение урав- нения (65) берется в виде
Цилиндрические функции Бесселя с соседними индексами и их произ- водные связаны между собой рекуррентными соотношениями
Отметим важный частный случай второй из формул (71) при v= 0
Третье из соотношений (72) может быть записано в интегральной форме
Наиболее часто употребляются цилиндрические функции с целыми индексами J 0(x), J 1(x), …, Jn (x), …, а также положительные нули этих функций. Всякое уравнение Jn (x)=0 имеет счетное множество положи- тельных корней:
или, что то же самое, функция Jn (x)имеет счетное множество положи- тельных нулей. Приведём вычисленные с точностью до четырех десятич- ных знаков значения первых шести нулей функции J 0(x):
Вспомним, что если коэффициент k (х) обращается в нуль при х =0, то появляется так называемый особый случай постановки задачи Штурма
Уравнение (65) может быть записано в эквивалентной форме:
и естественно, что оно соответствует особому случаю постановки крае-вых задач, когда k (x) =x, k (0)=0. Простейшая краевая задача для уравнения Бесселя возникает при изу- чении собственных колебаний круглой мембраны:
Здесь k (r) =r и весовая функция p (r) =r. Чтобы ее решить, полагаем x=λr, где x новая независимая переменная. Тогда
и уравнение (76) приводится к уравнению Бесселя
Общее решение этого уравнения представим формулой (70), а после возвращения к переменной r получим общее решение уравнения (76) в виде
Из (77) и (79) ясно, что Jn (0)=0, Nn (0)=∞, поэтому выполнимость первого из граничных условий (77)
означает, что С 2=0.Тогда полагаем С 1=1, и со второго граничного усло- вия находим собственные значения
Соответственно из (78) найдем собственные функции
Найденные собственные функции образуют ортогональную систему с весом r на отрезке [0, l ], т.е. выполнено условие ортогональности
и можно рассматривать ряды Фурье по системе (79):
Квадрат нормы собственной функции вычисляется точно и имеет значение
Отметим также частный случай (см. (42))
Довольно часто встречается и вторая краевая задача для уравнения Бесселя
И на этот раз общее решение уравнения (82) может быть записано в ви- де (78), снова получим С 2=0 и С 1=1, а собственные значения будут определяться из условия
где через
они образуют ортогональную систему с весом r на [0, l ], а квадрат нормы
229. Решите задачу о свободных колебаниях однородной круглой мемб- раны радиуса l, закрепленной по краю, если начальная скорость равна ну- лю, а начальное отклонение
Р е ш е н и е. Здесь нужно решать смешанную задачу
по методу Фурье, полагая После подстановки в дифференциальное уравнение и разделения переменных придем к равенству
Из условия
Вводя новую переменную
и его общее решение (см.(35))
Возвращаясь к переменной r, получим общий вид радиальной функции:
Из условия
тогда полагаем
Для временной функции T (t) имеем дифференциальное уравнение с постоянными коэффициентами
и его решение есть линейная комбинация
Умножая ее на собственную функцию и суммируя по всем k, получим ряд
Из второго начального условия получим
Первое начальное условие приводит к равенству
откуда с учетом (81) найдем (см.также (73))
где 230 Решите задачу о свободных колебаниях круглой мембраны радиуса l, закрепленной по краю и колеблющейся в среде, сопротивление которой пропорционально скорости, если Р е ш е н и е. Здесь нужно решать смешанную задачу
методом Фурье, полагая u (r,t) =R (r) T (t). Тогда после разделения перемен- ных в дифференциальном уравнении
С учетом граничных условий придем к задаче Штурма радиальной функции
и ее собственные значения и собственные функции, как и в предыдущей задаче, соответственно равны
Дифференциальное уравнение для временной функции при малом h
имеет решение
Составляем ряд
и подставляя его в начальное условие
Из второго граничного условия вытекает, что
В итоге придем к ответу
231. Уравнение малых продольных колебаний нити, подвешенной в кон- цевой точке x=l и колеблющейся под действием силы тяжести, имеет вид
Найдите u (x,t) при t >0если
Р е ш е н и е. Здесь возникает смешанная задача
Полагая u (x,t) =X (x) T (t) придем к соотношению
С учетом граничных условий, придем к задаче Штурма
ее собственные функции ортогональны с единичным весом на [0, l ]. Вве- дя новую переменную
соответственно преобразуется и задача Штурма
а ее собственные значения и собственные функции соответственно бу- дут
Дифференциальное уравнение для временной функции
поэтому составляем ряд
Подставляя его в первое начальное условие, найдем
причем для интеграла, стоящего в знаменателе, верно равенство
следовательно, окончательно имеем
Из второго начального условия вытекает, что Bk= 0, поэтому в ответе получим
232.Круглая однородная мембрана радиуса l закреплена по краю, нахо- дится в состоянии равновесия при натяжении Т 0. Найдите отклонение мембраны u (r,t) от положения равновесия, если к ней прилагается равно- мерно распределенная нагрузка Р е ш е н и е. Текстовая задача равносильна смешанной задаче
Найдем решение имеющегося дифференциального уравнения в виде
Относительно v (r) будем иметь обыкновенное дифференциальное урав- нение
частным решением которого будет, что нетрудно проверить, функция
и это частное решение удовлетворяет граничным условиям
|
|||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.45.223 (0.013 с.) |


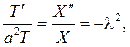 и из граничных условий найдем
и из граничных условий найдем




 Опреде-
Опреде-


 Лиувилля
Лиувилля
 найдем
найдем




 есть решение дифференциального урав- нения, удовлетворяющее граничным условиям, поэтому после замены
есть решение дифференциального урав- нения, удовлетворяющее граничным условиям, поэтому после замены






 в уравнение, будем иметь
в уравнение, будем иметь

 .Получим семейство задач Коши:
.Получим семейство задач Коши:
 Для четных k= 2 m все
Для четных k= 2 m все  будут равными нулю, и, следовательно, придем к отве- ту:
будут равными нулю, и, следовательно, придем к отве- ту:




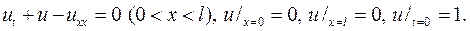








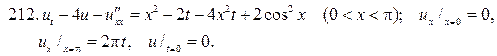






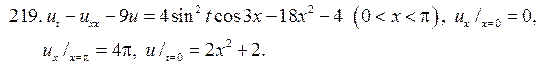









 (65)
(65) есть произвольное действительное или ком-плексное число,
есть произвольное действительное или ком-плексное число, 
 , то общее решение уравнения (65) есть линейная комбина- ция
, то общее решение уравнения (65) есть линейная комбина- ция (66)
(66) и
и  называются соответственно цилиндрическими функ- цииями Бесселя первого и второго рода, для которых имеются представ- ления в виде рядов
называются соответственно цилиндрическими функ- цииями Бесселя первого и второго рода, для которых имеются представ- ления в виде рядов
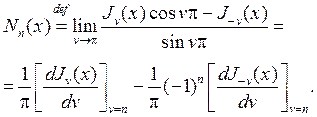


 (70)
(70)
 (72)
(72) (73)
(73)

 (74)
(74)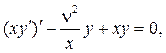 (75)
(75)


 (78)
(78)

 (79)
(79)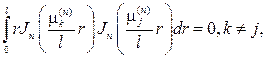

 (80)
(80) (81)
(81)

 обозначены положительные нули производной
обозначены положительные нули производной  Собственные функции задачи (82
Собственные функции задачи (82 





 найдем R (l)=0, а второе условие как в особом случае
найдем R (l)=0, а второе условие как в особом случае  поэтому придем к задаче Штурма
поэтому придем к задаче Штурма 
 будем иметь
будем иметь


 найдем
найдем
 откуда
откуда








 Подставляя найденные коэффициенты в ряд, придем к ответу
Подставляя найденные коэффициенты в ряд, придем к ответу
 положительные корни уравнения J 0(x)=0.
положительные корни уравнения J 0(x)=0.







 придем к равенству
придем к равенству








 , найдем
, найдем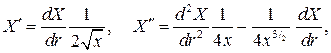


 имеет решение
имеет решение