
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специальности 1-31 04 01 «Физика»Стр 1 из 8Следующая ⇒
ЗАДАЧИ ПО МАТЕМАТИЧЕСКОЙ ФИЗИКЕ И ИХ РЕШЕНИЕ Пособие для студентов физического факультета Специальности 1-31 04 01 «Физика» МИНСК А в т о р ы – с о с т а в и т е л и: В. Н. Русак, Н. К. Филиппова
Рекомендовано Ученым советом физического факультета 28 июня 2005 г.протокол №11
Р е ц е н з е н т ы: доктор физико-математических наук, профессор В.Т. Ерофеенко; доктор физико-математических наук, профессор А. А. Пекарский.
Задачи по математической физике и их решения: пособие для студентов физ. спец. 1=310401 «Физика»/ авт.=сост. В.Н. Русак, Н.К. Филиппова. -Мн.: БГУ, 2006 г.-93 с.
Для студентов 1-2 курсов физического факультета и факультета радиофизики и электроники БГУ.
Предисловие Преподавание математических дисциплин на физических факультетах Белорусского государственного университета складывалось на основе опубликованного В.И. Смирновым пятитомного «Курса высшей матема- тики» В 1998 г. В.Н. Русак издал краткий курс математической физики рассчитанный на 90 лекционных часов. При написании настоящего посо- бия авторы, в доходчивой форме изложили круг основных идей и мето- дов применяемых при решении задач математической физики в рамках действующей программы. В нем по каждой теме приведены необходимые теоретические сведения, подробно разобраны решения типовых упражне- ний и предложены примеры для самостоятельной работы. Основной ак -цент делается на метод разделения переменных и применение цилиндри -ческих функций. Пособие адресовано студентам физикоматематических специаль- ностей которые изучают дифференциальные уравнения в частных произ- водных и их приложения.
РЯДЫ И ПРЕОБРАЗОВАНИЯ ФУРЬЕ Если f (x) 2 l – периодическая кусочно-гладкая функция на R, то она раскладывается в ряд Фурье
Бывает так, что функция f (x) задана и является кусочно-гладкой на отрезке [- l, l ]и ее также можно разложить в ряд Фурье вида (1-2), и сумма этого ряда будет 2l – периодическим продолжением функции f (x). Добавим к сказанному, что в формулах (2) в силу 2 l –периодичности можно вести интегрирование по любому отрезку длиной 2 l.
Если f (x) четная 2 l – периодическая кусочно-гладкая функция, то коэффициенты bk =0, и соответственно
Если f (x) нечетная 2 l – периодическая кусочно-гладкая функция, то коэффициенты ak =0, и соответственно
Если f (x) кусочно-гладкая функция на отрезке [0, l ], то ее можно разложить в ряд Фурье (3), (4), так и в ряд Фурье (5), (6), осуществляя соответствующее продолжение функции f (x). Если f (x) непрерывная 2 l – периодическая функция и существует кусочно-непрерывная производная f (x), то ряд Фурье функции f (x) сходится к ней равномерно. Для всякой кусочно-непрерывной на [- l, l ] функции выполняется ра- венство Ляпунова-Стеклова
Если f (x) кусочно-непрерывная функция на отрезке [- l, l ], то ее ряд Фурье можно интегрировать почленно. Предполагаем теперь, что f (x)определена на R, абсолютно интегриру- ема и является кусочно-гладкой на каждом конечном отрезке. Тогда спра- ведлива интегральная формула Фурье
Разумеется, что в точках непрерывности правая часть соотношения (8) может быть заменена на f (x). Интегральная формула Фурье равносильна выполнению двух пре- образований: прямого преобразования Фурье
и обратного преобразования Фурье
где х точка непрерывности и интеграл в (10) понимается в смысле главно- го значения по Коши. 1. Разложить в ряд Фурье функцию
Р е ш е н и е. Учитывая четность f (x), применяем формулу (4) и получим при k ³1
Если же k =0, то
Cледовательно, на интервале
2. Разложить в ряд Фурье функцию f (x) = arсsin(sin x), xÎ R. Р е ш е н и е. Поскольку:
то f (x) нечетная функция на R, а период функции равен 2p. В качестве основного отрезка можно брать отрезок [-p,p] и применять формулу (6). Предварительно нужно учесть, что
Если же f (x)=arcsin (sin(p- x))=p -x. Следовательно для коэффициентов Фурье будем иметь по формулам (6)
Следовательно для всех x Î R имеет разложение в ряд
3. Проверьте, что при 0< x <p выполнено равенство
Р е ш е н и е. Продолжим функцию
нечетным образом на (-p,0) и разложим в ряд Фурье (5),(6). Будем иметь
Итак, мы проверили, что 4. Разложите в ряд Фурье функцию
Р е ш е н и е. Поскольку f (x) определена на R, нечетная, имеет период 2pи является гладкой, то она разлагается в ряд (5),(6), однако коэффици- енты будем находить не по формулам (6). Воспользуемся известным сте- пенным рядом
Левую часть равенства в числителе и знаменателе домножим на
и если в этом соотношении отделить слева и справа мнимые части, то получим
5. Найдите преобразование Фурье для функции Р е ш е н и е. Пользуясь формулой (9) и леммой Жордана будем иметь при a>0
Если же a<0, то интеграл считается через вычет в точке ai и получим
Объединяя обе формулы, найдем Разложите в ряды Фурье в указанных интервалах: 6. f (x)= x в интервале(-l, l). 7. f (x)=sign x в интервале (-l, l). 8. f (x) = cos4 x, x Î(-¥,¥). 9. f (x) =|x|, x Î(-l, l). 10. f (x) =l 2 -x 2 в интервале (-l, l). 11. f (x) =x 2 в интервале (-p,p).
13. f (x)= | sin x|, x Î(-¥,¥). 14. f (x)= | cos x|, x Î(-¥,¥). 15. f (x) = sign(cos x), x Î(-¥,¥). 16. f (x) = arcsin(cos x), x Î(-¥,¥). 17. f (x) =x -[ x ], xÎ (-¥,¥). 18. Функцию f (x) =x 2 разложить в ряд Фурье а) по косинусам б) по синусам в) в интервале (0,2 l).
Используя эти разложения, найти суммы числовых рядов
19. Отправляясь от разложения
найти интегрированием разложения в ряд Фурье на интервале 20. Напишите равенство Ляпунова для функции
21. Вычислить с помощью равенства Ляпунова интеграл
Найдите разложения в ряды Фурье с помощью степенных рядов для следующих 2p-периодических функций:
Докажите равенства:
27. 28. Как нужно продолжить функцию f (x) с интервала 29. Как нужно продолжить функцию f (x) с интервала (-p,p), чтобы выполнялась равенство Найдите преобразования Фурье от следующих функций:
36. 37. 38. Найдите четное и нечетное преобразование Фурье для функции
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ Комплекснозначная функция действительной переменной f (t) называ- ется оригиналом по Лапласу, если 1) f (t)=0 при t <0, 2) на любом конечном отрезке [0, t ] f (t) и ее производные 3) f (t) растет не быстрее показательной функции, а именно Преобразованием Лапласа называется функция комплексной переменной
Для всякого оригинала f (t) преобразование Лапласа F (p) существует и является аналитической функцией в полуплоскости Re p>S 0. Наряду с термином преобразование Лапласа употребляют термин из-ображение, т. е. говорят, что всякому оригиналу f (t) по формуле (11) ста- вится в соответствие изображение F (p). Кроме того, употребительна за- пись f (t) ≓ F (p) или F (p) ≓ f (t), означающая, что f (t) по изображению равна F (p), или точнее: F (p)есть изображение для оригинала f (t). Имея дело с конкретными оригиналами, будем задавать их только при t ³ 0, помня о том, что при t <0 оригиналы равны нулю. Перечислим основные свойства оригиналов и изображений 1. Линейность. Изображение линейной комбинации равно линейной комбинации изображений
2. Дифференцирование оригинала. Если f (t) и ее производные
и при любом n
3. Интегрирование оригинала. Если f (t) ≓ F (p), то
4. Дифференцирование изображения. Если f (t) ≓ F (p), то при любом n
5. Интегрирование изображения. Если f (t)≓ F (p), и существует интег- рал
6. Теорема запаздывания. Если f (t) ≓ F (p), и τ>0, то
7. Теорема смещения. Если f (t) ≓ F (p), то при любом комплексном p 0
8. Теорема о свертке. Если f (t) ≓ F (p), g (t) ≓ G (p), то
9. Теорема разложения. Если f (t) ≓ F (p), изображение F (p) аналитично всюду, за исключением конечного числа особых точек в конечной части плоскости, и F (p)→0 равномерно относительно аргумента при р → ¥, то
где сумма вычетов берется по всем особым точкам функции F (p). Свойства дифференцирования и интегрирования оригиналов позволя- ют сводить названные операции соответственно к умножению и делению на р. На этих свойствах основано применение операционного исчисления к решению дифференциальных, интегральных и интегродифференциаль- ных уравнений и их систем, которые встречаются в радиотехнике. 39. Найдите изображения по заданным оригиналам а) г) ж) к) Р е ш е н и е. а) По формуле (11) имеем
б) По формуле (11)
в) Опираясь на формулы Эйлера, свойство линейности и предыдущий пример, будем иметь
г) Изображение функции cos wt может быть найдено аналогично как и для sin wt, или можно воспользоваться дифференцированием оригинала, т. е. формулой (12) sin wt ≓ д) Применяя свойство дифференцирования изображения, имеем 1 ≓ е) Отправляясь от изображения функции sin t и применяя формулу (16), будем иметь sin t ≓
ж) Применяя формулу (14), получим
з) С учетом теоремы смещения
и) Применяя теорему смещения, будем иметь
к) Пользуясь определением и выполняя замену переменной интегрирования, найдём
40. Найдите оригиналы по заданным изображениям а) в) Р е ш е н и е. а) После выделения полного квадрата имеем
Здесь применена теорема смещения, поскольку б) Поскольку sin3 t ≓
в) Раскладываем F (p) на простые дроби и пользуемся свойствами линейности
г) По теореме разложения имеем
41. Решите задачу Коши
Решение. Полагая x (t) ≓ X (p), найдем с учетом (13)
Учитывая еще, что cos t ≓
откуда следует, что
или после разложения на простые дроби, будем иметь
≓ 42. Решите интегральное уравнение
Р е ш е н и е. Полагая j(х) ≓F(р), учитывая, что cos t ≓
Откуда найдем с учетом теоремы смещения
≓ 43. Найдите частное решение интегро-дифференциального уравнения
Р е ш е н и е. Пользуясь теоремой о свертке и свойством дифференцирования оригинала, найдем
Отсюда получим
≓
44. Докажите равенство
где в левой части находится интеграл вероятности
Р е ш е н и е. Введем вспомогательную функцию
и убедимся, что она удовлетворяет дифференциальному уравнению
Действительно, имеем
С учетом того, что f (0)=0и
Итак, мы нашли, что
Вспоминая теорему смещения, окончательно находим
45. Пользуясь формулой
найдите операционным способом решение краевой задачи
Р е ш е н и е. Применяем преобразование Лапласа по переменной t
и приходим к краевой задаче для обыкновенного дифференциального уравнения второго порядка
причем нам нужно искать ограниченное в окрестности точки
Пользуясь определением и свойствами оригиналов и изображений, найдите изображения следующих оригиналов 46. 49. 52. 55. 58. 61. 64. 67. 70. 73. 76. 78. 80. 82. Пользуясь свойствами оригиналов и изображений, разложением изображения на простые дроби или теоремой разложения, найдите оригиналы по заданным изображениям: 83. 85. 87. 89. 91.
Найдите решения дифференциальных и интегральных уравнений, удовлетворяющих заданным условиям 95. 96. 97. 98. 99. 100. 101. 102. 103. 104. 105. 106. 107. 108. 109. 110. 111. 112. 113. 114. 116. 118. 120.
КЛАССИФИКАЦИЯ И ПРИВЕДЕНИЕ ПРОСТЕЙШИЙ ВАРИАНТ МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ Рассмотрим смешанную задачу для однородного уравнения колебаний струны:
Будем искать решение в форме u (x,t) = X (x) T (t). (34) Подставляя (34) в (31) и разделяя переменные, получим соответст- венно
Поскольку это должно быть тождеством, то на самом деле его левая часть не зависит от t, а правая часть не зависит от x, их следует приравнять к некоторой константе так, что имеем
С другой стороны, подставляя (34) в (32), найдем
Если T (t) = 0,то из (34) вытекает u (x,t) = 0, а нам нужно искать нетриви- альные решения уравнения (31). Стало быть, T (t)¹0 и из (36) имеем гра -ничные условия для функции Х (х) в виде Х (0) =Х
Подлежат нахождению функция Х (х) и параметр Определение. Те значения параметра
С учетом названного определения говорят, что решить задачу Штур- ма Общее решение уравнения (37) как линейного уравнения с постоянны- ми коэффициентами запишется в виде
Добиваясь выполнения граничных условий (38), имеем С 1 × 1 + С 2 × 0 = 0 Þ С 1=0. Если С 2=0, то придем к тривиальному решению Х (х)º0, поэтому С 2¹0 и пусть для определенности С 2=1. Из второго граничного условия выте -кает, что sin l
Теперь возвращаемся к равенству (35) и берем дифференциальное уравнение для функции Т (t) при
Его общее решение будет иметь вид
где Согласно (34) произведения собственных функций (39) на соответству- ющие решения
будут решать задачу (31 Более того, ряд
если только он допускает двойное почленное дифференцирование по пе- ременным – x и t, также будет решением задачи (31 Подставляя (40) в (33), будем иметь
откуда по формулам для коэффициентов Фурье получим
Из второго граничного условия найдем, что
и, стало быть,
Мы получили, что сумма ряда (40) будет решением исходной задачи (31) ние (см. [1]), и его сумма будет классическим решением задачи (31) Изложенная схема решения смешанной задачи принципиально не ме-няется и при других однородных граничных условий. Считается целесо-образным запоминать метод решения, а не его детали, поэтому при реше- нии примеров с конкретными граничными функциями полняются те же самые действия (или аналогичные при измененных граничных условиях (32)) и в той же последовательности, что и при об- щих начальных условиях (33). Заметим, что такая традиция соблюдается в целом при решении дифференциальных уравнений. 144.Однородная струна, жестко закрепленная в концевых точках x =0 и
Определить смещение u (x,t) точек струны от прямолинейного положе- ния равновесия, предполагая, что начальные скорости отсутствуют. РЕШЕНИЕ СМЕШАННОЙ ЗАДАЧИ ИЛИ В ГРАНИЧНЫХ УСЛОВИЯХ Будем рассматривать смешанную задачу
и будем искать ее решение в виде суммы двух функций u (x,t) =v (x,t) +w (x,t), которые находятся из решения более простых задач. Функция v (x,t) у довлетворяет неоднородному уравнению с нулевыми граничными и начальными условиями
Соответственно функция w (x,t) есть решение смешанной задачи
Нам нужно решать только штрихованную задачу (43¢)
Функцию v (x,t) следует разыскивать в виде ряда по собственным функ-
циям задачи (7-8) Штурма
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.175.182 (0.269 с.) |
 и серии учебных пособий
и серии учебных пособий  , отражающих опыт преподава- ния в московских вузах. Что касается непосредственно математической физики, то на русском языке также имеется ряд учебных пособий и сбор- ников задач
, отражающих опыт преподава- ния в московских вузах. Что касается непосредственно математической физики, то на русском языке также имеется ряд учебных пособий и сбор- ников задач  .
. (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9)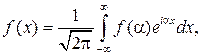 (10)
(10)



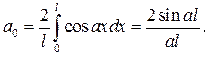
 выполнено равенство
выполнено равенство


 то sin x =sin (p- x) и тогда
то sin x =sin (p- x) и тогда








 и тем самым устано- вили нужное равенство.
и тем самым устано- вили нужное равенство.


 , тогда будем иметь
, тогда будем иметь

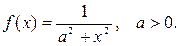
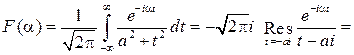

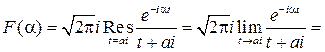
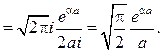

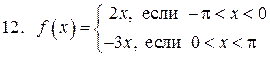




 ,
, функций х 2, х 3, х 4.
функций х 2, х 3, х 4.






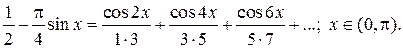
 на интервале (-p,p), чтобы выполнялось равенство
на интервале (-p,p), чтобы выполнялось равенство 
 на интервал
на интервал






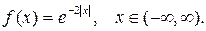

 продолжая ее четным или нечетным способом.
продолжая ее четным или нечетным способом.

 суть кусочно-непрерывные функции,
суть кусочно-непрерывные функции,
 - показатель роста оригинала.
- показатель роста оригинала. (11)
(11) ≓
≓ 
 суть оригиналы, то справедливы формулы
суть оригиналы, то справедливы формулы ≓
≓  (12)
(12) ≓
≓  (13)
(13) ≓
≓  (14)
(14) ≓
≓ 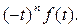 (15)
(15) то
то ≓
≓  (16)
(16) ≓
≓  (17)
(17) ≓
≓  (18)
(18) ≓
≓  (19)
(19) (20)
(20)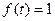 б)
б) 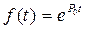 в)
в) 
 д)
д)  е)
е) 
 з)
з)  и)
и) 
 .
. ≓
≓ 
 ≓
≓  .
.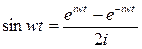 ≓
≓ 
 ≓
≓  .
. ≓
≓  ≓
≓  .
. ≓
≓  ≓
≓ 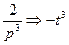 ≓
≓ 
 ≓
≓  ≓
≓ 
 ≓
≓ 
 ≓ arcctg p.
≓ arcctg p. ≓
≓  ≓
≓  .
. ≓
≓  ≓
≓  .
.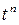 ≓
≓  ≓
≓  .
. ≓
≓ 


 ≓
≓ 
 , б)
, б)  ,
, , г)
, г)  .
. ≓
≓  .
. ≓
≓  .
. , то по формуле (15)
, то по формуле (15) ≓
≓  ≓
≓ 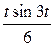 .
. ≓
≓ 










 ≓
≓ 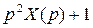 ,
,  ≓
≓ 
 , придем к операторному уравнению
, придем к операторному уравнению

 ≓
≓  ≓
≓
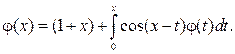
 и формулу (19), придем к операторному уравнению
и формулу (19), придем к операторному уравнению


 ≓
≓


 ≓
≓
 ≓
≓ 

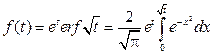


 ≓
≓  перейдем к операторному урав- нению
перейдем к операторному урав- нению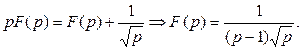
 ≓
≓ 
 ≓
≓  ≓
≓ 
 ≓
≓ 

 ≓
≓  ≓
≓ 
 ≓
≓ 
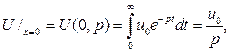

 решение. Таковым решением будет, очевидно, функция
решение. Таковым решением будет, очевидно, функция ≓
≓ 
 . 47.
. 47.  48.
48. 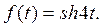
 50.
50.  51.
51. 
 53.
53.  54.
54. 
 56.
56.  57.
57. 
 59.
59.  60.
60. 
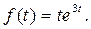 62.
62.  63.
63. 
 65.
65. 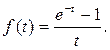 66.
66. 
 68.
68.  69.
69. 
 71.
71.  72.
72. 
 74.
74. 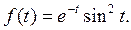 75.
75. 
 77.
77. 
 79.
79. 
 81.
81.  .
.
 84.
84. 
 86.
86. 
 88.
88. 


 92.
92. 









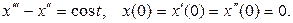











 115.
115. 
 117.
117. 
 119.
119. 
 121.
121. 

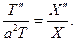
 (35)
(35) (36)
(36)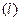 = 0. Присоединяя эти граничные условия к дифференциальному уравнению для функции Х (х), из соотношения (35) получим так называемую задачу Штурма
= 0. Присоединяя эти граничные условия к дифференциальному уравнению для функции Х (х), из соотношения (35) получим так называемую задачу Штурма  Лиувил- ля
Лиувил- ля
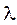 . Очевидно, что при любых
. Очевидно, что при любых  имеет тривиальное решение Х (х)º0, но есть еще и нетривиальные решения по крайней мере при некоторых
имеет тривиальное решение Х (х)º0, но есть еще и нетривиальные решения по крайней мере при некоторых  Лиувилля
Лиувилля 
 =0 и, следовательно
=0 и, следовательно 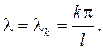 Соответствующие собст -венные функции примут вид
Соответствующие собст -венные функции примут вид (39)
(39) :
:

 и
и  – произвольные постоянные.
– произвольные постоянные.
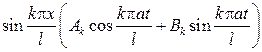
 32) при любых
32) при любых  и
и  (40)
(40)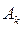 и
и 
 (41)
(41)
 (42)
(42) (33), если коэффициенты
(33), если коэффициенты  и
и  и
и  ряд (40) будет допускать двойное почленное дифференцирова-
ряд (40) будет допускать двойное почленное дифференцирова- вы-
вы- , имеет в начальный момент времени t =0 форму
, имеет в начальный момент времени t =0 форму



 (33), и следовательно (см.(40)
(33), и следовательно (см.(40) 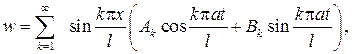
 (46)
(46) (47)
(47)


