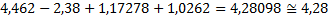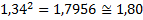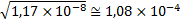Правила приближённых вычислений

Числовые значения технических величин являются большей частью приближенными. Точность рассчитываемых технических величин определяется точностью исходных (часто эмпирических) данных.

Рассмотрим такой пример. Пусть требуется определить сопротивление R некоторого проводника. При измерении вольтметром с точностью до 0,01В определили напряжение на концах этого проводника В. Затем, амперметром с точностью до 0,01А измерили протекающий по этому проводнику ток А.

Без критического подхода к вычислениям можно получить такой результат:

Но так как числа 9,38 и 3,46 приближенные, то последние цифры в этих числах сомнительные. При измерении с указанной выше точностью могла быть допущена ошибка на 0,01 как в сторону увеличения напряжения, так и в сторону его уменьшения; то же самое в отношении тока.

Таким образом, сопротивление проводника, если его вычислять с точностью до пятого десятичного знака, как это сделано выше, могло оказаться

Сравнение всех трех результатов показывает, что они отличаются уже вторыми десятичными знаками и что достоверным (надежным) является лишь первый десятичный знак, а второй десятичный знак – сомнительным (не вполне надежным). Цифры, выражающие остальные десятичные знаки, – совершенно случайные.

Во избежание накапливания вычислительной ошибки принято определять, кроме достоверных знаков, ещё только один сомнительный. В рассмотренном примере необходимо было проводить вычисление до второго десятичного знака:

 

Правила выполнения приближённых вычислений

1. При сложении (вычитании) приближённых чисел окончательный результат округляют так, чтобы он не имел значащих цифр[1] в тех разрядах, которые отсутствуют хотя бы в одном из слагаемых.

2. При умножении (делении) следует округлять сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом таких цифр.

В окончательном результате необходимо оставлять такое же число значащих, цифр, какое имеется в сомножителях, после их округления. В промежуточных результатах следует сохранять на одну значащую цифру больше.

3. При возведении в степень в основании степени.

4. При извлечении корня следует в полученном результате брать столько значащих цифр, сколько их имеется в подкоренном выражении.

5. При вычислении сложных выражений следует применять указанные выше правила в соответствии с видом производимых действий.

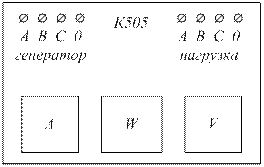
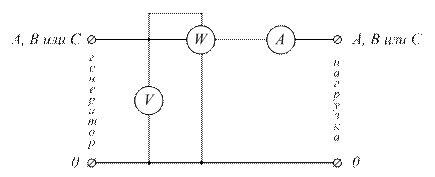
Сомножитель 5,1 имеет наименьшее число значащих цифр – две, поэтому конечный результат округляется до двух значащих цифр, а результаты всех промежуточных вычислений должны округляться до трёх значащих цифр.

Приложение 2

Измерительный комплект К505

Измерительный комплект К505 содержит амперметр A, ваттметр W, вольтметр V.

Рис. П.1. Принципиальная схема измерительного комплекта К505:
А, В, С – точки подключения соответствующих фаз цепи;
0 – точка подключения нулевого провода.

Рис. П.2. Принципиальная схема соединения приборов при однофазных измерениях

Каждый прибор измерительного комплекта К505 имеет изменяемую цену деления.

Приложение 3

Образец титульного листа

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»

Институт кибернетики, информатики и связи
Кафедра «Электроэнергетика»

 

 

ОТЧЁТ
по лабораторной работе № ___

_____________________________________________________

(тема лабораторной работы)

 

 

Выполнил: ст. гр. ГРУППА-ХХ
Фамилия Имя

Проверил: ассистент каф. ЭЭ
Ф.И.О.

 

Тюмень 2012

[1]Значащими цифрами называются все цифры, кроме нуля, а также и нуль в двух случаях:

1) когда нуль стоит между значащими цифрами;

2) когда нуль стоит в конце числа и когда известно, что единиц соответствующего разряда в данном числе не имеется.