
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное решение систем нелинейных уравненийСодержание книги
Поиск на нашем сайте
Постановка задачи. Требуется решить систему нелинейных уравнений Убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение в случае системы двух уравнений с двумя неизвестными можно, построив графики функций в удобных координатах. В случае сложных функций можно посмотреть поведение аппроксимирующих их полиномов. Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет. Метод Ньютона. Обозначим
Это можно интерпретировать как первые два члена разложения функции в ряд Тейлора вблизи
Мы получили систему линейных уравнений, неизвестными в которой выступают величины
где в данном случае
Критерием окончания итерационного процесса является условие Блок-схема метода Ньютона для решения систем нелинейных уравнений.
Так как метод Ньютона отличается высокой скоростью сходимости при выполнении условий сходимости, на практике критерием работоспособности метода является число итераций: если оно оказывается большим (для большинства задач >100), то начальное приближение выбрано плохо.
Частным случаем решения (4) методом Ньютона системы из двух нелинейных уравнений
являются следующие легко программируемые формулы итерационного процесса:
Метод простых итераций. Метод простых итераций для решения (1) аналогичен методу, рассмотренному при решении нелинейных уравнений с одним неизвестным. Прежде всего, выбирается начальное приближение
и по ней осуществляется итерационный цикл. Если итерации сходятся, то они сходятся к решению уравнения (1). Обозначим Например, для исходной системы уравнений
где множители
Метод спуска. Рассмотрим функцию Поиск минимума функций. Задачи поиска максимума эквивалентны задачам поиска минимума, так как требуется лишь поменять знак перед функцией. Для поиска минимума необходимо определить интервал, на котором функция могла бы иметь минимум. Для этого можно использовать (1) графическое представление функции, (2) аналитический анализ аппроксимирующей функции и (3) сведения о математической модели исследуемого процесса (т.е. законы поведения данной функции).
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.36 (0.005 с.) |

 (1). В координатном виде эту задачу можно записать так:
(1). В координатном виде эту задачу можно записать так:  , где 1 ≤ k ≤ n.
, где 1 ≤ k ≤ n. некоторое приближение к корню системы уравнений
некоторое приближение к корню системы уравнений  . Пусть малое
. Пусть малое  . Вблизи
. Вблизи  , 1 ≤ k ≤ n. (2)
, 1 ≤ k ≤ n. (2) . В соответствии с (1), приравнивая (2) к нулю, получим:
. В соответствии с (1), приравнивая (2) к нулю, получим: , 1 ≤ k ≤ n. (3)
, 1 ≤ k ≤ n. (3) . Решив ее, например, методом Гаусса, мы получим некое новое приближение к
. Решив ее, например, методом Гаусса, мы получим некое новое приближение к  . Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона, рассмотренного в предыдущей главе:
. Выражение (3) можно представить как обобщение на систему уравнений итерационного метода Ньютона, рассмотренного в предыдущей главе: , (4)
, (4) – матрица Якоби, которая считается для каждого (s) приближения.
– матрица Якоби, которая считается для каждого (s) приближения. (Можем принять под
(Можем принять под  как норму
как норму  , так и
, так и 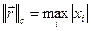 ). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если
). Достоинством метода является высокая скорость сходимости. Сходимость метода зависит от выбора начального приближения: если  , то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.
, то итерации сходятся к корню. Недостатком метода является вычислительная сложность: на каждой итерации требуется находить матрицу частных производных и решать систему линейных уравнений. Кроме того, если аналитический вид частных производных неизвестен, их надо считать численными методами.

 , где
, где  ,
, ,
, 
 , а исходная система уравнений преобразуется к эквивалентной системе вида
, а исходная система уравнений преобразуется к эквивалентной системе вида , (5)
, (5) . Достаточным условием сходимости является
. Достаточным условием сходимости является  . Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций
. Скорость сходимости метода сильно зависит от вида конкретно подбираемых функций  , которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса.
, которые должны одновременно удовлетворять условиям эквивалентности (5) и (1), и обеспечивать сходимость итерационного процесса. эквивалентная итерационная система (5) может быть представлена в следующем виде:
эквивалентная итерационная система (5) может быть представлена в следующем виде: ,
, = –0.15и
= –0.15и  = –0.1 подбираются из анализа условий сходимости.
= –0.1 подбираются из анализа условий сходимости. . Она неотрицательна и обращается в нуль в том и только в том случае, если
. Она неотрицательна и обращается в нуль в том и только в том случае, если  , то полученные значения
, то полученные значения  как раз и будут решениями уравнения (1). Подробнее о решении таких задач см. следующую главу.
как раз и будут решениями уравнения (1). Подробнее о решении таких задач см. следующую главу.


