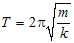Колебательное движение и его характеристики

Рис. 1

Механические колебания – это повторяющееся движение, при котором тело многократно проходит одно и то же положение в пространстве. Различают периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени.

Примерами механических колебаний могут служить движение шара на пружине, на нити, движение ножек звучащего камертона или молекул воздуха вблизи него (рис. 1). В физике рассматривают и другие колебания – процессы, обладающие той или иной степенью повторяемости во времени (например, электромагнитные колебания.)

Колебания можно классифицировать по условиям возникновения (свободные, вынужденные, автоколебания) и по характеру изменения во времени кинематических характеристик (пилообразные, гармонические, затухающие).

Если колебания совершаются в системе за счет первоначально сообщенной энергии, то они называются свободными. Примером таких систем являются модели колеблющихся тел: математический маятник и пружинный.

Математический маятник – колеблющаяся материальная точка, подвешенная на невесомой и нерастяжимой нити. К этой модели ближе всего массивное тело (шар), размер (диаметр) которого много меньше длины нити. Если его отклонить от положения равновесия, увеличив при этом потенциальную энергию системы «шар–нить», то будут наблюдаться колебательные движения этой системы. Колебательное движение системы «шар–нить» будет наблюдаться и в том случае, если шару сообщить кинетическую энергию, т.е. заставить его двигаться.

Рассмотрев малые колебания математического маятника (рис. 4), при которых отклонение его от положения равновесия х (t) << L, можно получить выражение для периода его колебаний. Как мы знаем, в любой момент времени для этой системы выполняется закон сохранения механической энергии:

Выразив высоту h через координату x по оси 0 Х (рис. 4, а) и учитывая, что при малых значениях х угол между нитью и вертикалью тоже мал, используем что для такого угла отклонения соотношение sin a» a» tg a.

Поэтому можно утверждать что малые колебания математического маятника происходят по гармоническому закону

x = A sin (w t + j₀),

где

,

т.е. с периодом

По гармоническому закону y = A sin (w t + ĵ₀) колеблется и пружинный маятник, состоящий из груза массой m и пружины жесткостью k (рис. 5).

Рис. 5

При этом период его колебания равен

Если горизонтальный пружинный маятник колеблется относительно положения равновесия, где пружина не растянута, то вертикальный пружинный маятник колеблется относительно положения равновесия, где ky ₀ = mg.

Период и частота свободных гармонических колебаний в обоих случаях определяются только собственными параметрами системы: длиной нити математического маятника или жесткостью пружины и массой груза пружинного маятника, поэтому свободные колебания часто называют собственными колебаниями, а частоту, с которой они происходят, собственной частотой колебаний системы.