Расскажите о принципе получения геометрических атрибутов – наклонов и азимутов падения сейсмических границ.(стр.221)

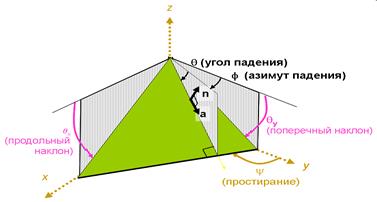
Геометрические атрибуты применяются для решения структурных задач. Основой для определения геометрических атрибутов служат 2D и 3D сейсмические изображения и выделяемые по ним сейсмические поверхности. Некоторые из методов анализа изображений заимствованы из других отраслей, решающих подобные задачи (анализ аэрокосмических изображений, криминалистика и пр.). В принципе всю интересующую структурную информацию можно разделить на две части. Регулярную (когерентную) часть, связанную с отражающими границами, и нерегулярную (некогерентную) часть, связанную с перерывами регулярности отражений в местах разрывных нарушений, наличием неоднородностей небольших по сравнению с длиной волны размеров (каналы, русла и пр.). В свою очередь, когерентная информация может потребовать более подробной дифференциации, отображающей характер отражающих границ, изменения их наклонов и азимутов падения, кривизны и пр. В некоторых случаях сведения о разрывных нарушениях малой амплитуды можно получить, только детально изучая особенности поведения отражающих границ.

К определению атрибутов угла и азимута падения отражающей границы:

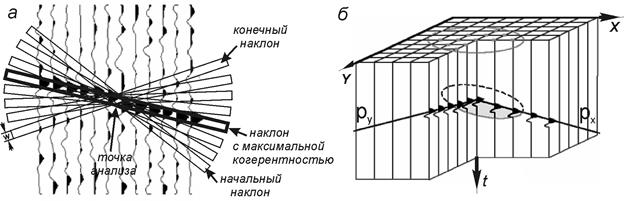
Принцип разделения информации на когерентную и некогерентную часть положен в основу различных способов анализа сейсмических изображений. Простейший способ анализа 2D сейсмических изображений можно представить в виде их сканирования небольшими, включающими несколько трасс, прямоугольными временными окнами шириной W, рассчитанными на то, что локальные участки отражающих границ можно считать плоскими. В заданной точке анализа (x, t) окно поворачивается относительно своего центра с некоторым шагом в пределах выбранных начальных и конечных наклонов (см. следующий слайд а). При каждом наклоне производится расчет когерентности информации, находящейся в пределах окна. Точке анализа присваивается значение наклона, соответствующее наклону окна с максимальной когерентностью, поскольку окна с наибольшей когерентностью, совпадают с осями синфазности отражений. Подобный анализ для всех точек матрицы разреза позволяет получить атрибут наклонов отражающих границ.

 

Принципы получения геометрических атрибутов:

а - 2D случай,

б - 3D случай.

Подобный подход дает больший эффект при анализе объемных изображений, поскольку возникает возможность классифицировать отражения не только по наклону, но и по азимуту падения. Для этого можно использовать окно анализа в виде круга, центрированного относительно точек анализа и пересекающего определенное количество трасс (рис. 2.1,б). Время t в центре окна и кажущиеся наклоны p_x и p_y в направлениях x и y определяют локальную плоскую ось синфазности, максимальное истинное падение которой будет определяться как

p_max = (p_x² + p_y²)^1/2 (2.2)

Сканирование таким окном 3D изображения при неизменном положении центра окна и различных значениях p_x и p_y позволяет выделить угол падения и азимут падения плоскости наибольшей когерентности и получить истинный наклон и азимут отражений для заданного положения центра (следующий слайд). Подобный анализ с центрами во всех точках объемной матрицы дает возможность получить объемные атрибуты наклонов и азимутов границ. Для определения 3D когерентности используются также комплексные трассы и анализ проводится во временном окне W. Формула определения когерентности имеет тот же смысл, как и выражение (2.1), но она усложнена из-за объемного варианта анализа.