
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отделение изолированных корней уравнения с помощью компьютерной программыСодержание книги
Поиск на нашем сайте Пример №1 Отделить изолированные корни следующего уравнения с помощью компьютерной программы:
Найдем ООФ: подкоренное выражение должно быть строго больше нуля 0.
Отсюда ООФ: любые числа строго большие -1.75. Примем интервал [-1.75;150]; подставим значения в программу:
Рис. 1. Скриншот решения примера №1
Ответ: на интервале [-1.75;150] содержится 2 корней, на интервалах:
Пример №2 Отделить изолированные корни следующего уравнения с помощью компьютерной программы на интервале [-10;10]: Подставим имеющиеся данные в программу:
Рис. 3. Скриншот решения примера №2
Ответ: на интервале [-10;10] содержится 8 корней, на интервалах:
Уточнение корней с заданной точностью методом дихотомии Пример №1 Решить следующее уравнение методом дихотомии:
Рис. 1. Графики функций -0,5x и х2-3 Исходя из графиков, интервалы будут: [-2;0] и [0;2]. Подставим данные в программу:
Рис. 2. Скриншоты решения примера №1 Ответ: уравнение имеет 2 корня на интервалах:
Пример №2 Решить следующее уравнение методом дихотомии:
Рис. 3 Графики функций x2 и 1/2x Интервалы с корнями будут: [-3;-1] и [0;2]. Подставим полученные данные в программу:
Рис. 4. Скриншот решения примера №2 Ответ: уравнение имеет 2 корня на интервалах:
Уточнение корней с заданной точностью методом хорд Пример №1 Для уравнения Производная равна: Решим квадратное уравнение:
Корни уравнения: x1=0; x2= -0.5; x3= 0.5;
Сузим интервалы:
Интервалы будут следующими: [-2;-0,5] и [0,5;2]. Подставим данные в программу:
Рис. 1. Скриншоты решения примера №1 Ответ: на полученных интевалах для уравнения содержится 2 корня:
Пример №2 Для уравнения Производная равна: Решим квадратное уравнение:
Корни этого квадратного уравнения: x1=0; x2= -4; x3= 1.
Сузим интервалы:
Интервалы будут следующими: [-6;-4] и [1,4]. Подставим данные в программу:
Рис. 2. Скриншоты решения примера №2 Ответ: на полученных интевалах для уравнения содержится 2 корня:
Уточнение корней с заданной точностью объединенным методом Пример №1 Решить уравнение объединенным методом
Рис. 1. Графики функций 0.5x-3 = (х+2)2 Интервал для нахождения корней: [-2;1]. Подставим полученные значения в программу:
Рис. 2. Скриншот решения примера №1 Ответ: на интервале [-2;1] уравнение имеет корень х1 = -1.644 Пример №2 Решить уравнение объединенным методом
Рис. 3 Графики функций x2– 3 и -0.5x Выделим 2 интервала, содержащих корни: [-2;0] и [0;2]. Подставим полученные значения в программу:
Рис. 4. Скриншот решения примера №2 Ответ: на интервале [-2;0] уравнение имеет корень х1 = -0.999; интервале [0;2] уравнение имеет корень х2 = 1.637
Уточнение значения изолированного корня методом касательных Пример №1 Для уравнения Производная равна: Решим квадратное уравнение:
Корни этого квадратного уравнения: x1=0; x2= -4; x3= 1.
Сузим интервалы:
Интервалы будут следующими: [-6;-4] и [1,4]. Подставим данные в программу:
Рис. 1. Скриншоты решения примера №1 Ответ: на полученных интевалах для уравнения содержится 2 корня:
Пример №2 Для уравнения Производная равна: Решим квадратное уравнение:
Корни уравнения: x1=0; x2= -0.5; x3= 0.5;
Сузим интервалы:
Интервалы будут следующими: [-2;-0,5] и [0,5;2]. Подставим данные в программу:
Рис. 2. Скриншоты решения примера №2 Ответ: на полученных интевалах для уравнения содержится 2 корня:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.164.21 (0.008 с.) |





















 уточнить значение корня методом хорд.
уточнить значение корня методом хорд.




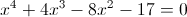 уточнить значение корня методом хорд.
уточнить значение корня методом хорд.


















