
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод екстраполяції економічної динаміки на основі кривих зростання.
2. Поліноміальні, експоненційні і Основна мета побудови трендових моделей економічної динаміки – на їх основі зробити прогноз про розвиток досліджуваного процесу на майбутнє. Прогнозування на основі часового ряду економічних показників належить до одномірним методів прогнозування, що базуються на екстраполяції, тобто на продовженні тенденції, що спостерігалася в минулому. При такому підході передбачається, що прогнозований показник формується під впливом великої кількості факторів, виділити які або неможливо, або по які відсутня інформація. У цьому випадку хід зміни даного показника пов’язують не з чинниками, а з плином часу, що проявляється в утворенні одновимірних часових рядів. Використання методу екстраполяції на основі кривих зростання для прогнозування базується на двох припущеннях: – часовий ряд економічного показника дійсно має тренд, тобто переважну тенденцію; – загальні умови, що визначали розвиток показника в минулому, залишаться без істотних змін протягом періоду випередження. Існує декілька типів кривих зростання, які можна використовувати для моделювання економічних процесів. Щоб правильно підібрати найкращу криву зростання для моделювання і прогнозування економічного явища, необхідно знати їх особливості. Найчастіше в економіці використовуються поліноміальні, експоненційні і
Параметр Для полінома першого степеня характерний постійний закон зростання. Якщо розрахувати перші прирости за формулою Якщо перші прирости розрахувати для полінома другого степеня, то вони будуть мати лінійну залежність від часу і ряд з перших приростів Для полінома третього степеня перші прирости будуть поліномами другого степеня, другі прирости будуть лінійною функцією часу, а треті прирости, що розраховуються за формулою
Поліноміальні криві зростання мають наступні властивості: - від полінома високого порядку можна шляхом розрахунку послідовних різниць (приростів) перейти до полінома нижчого порядку; - значення приростів для поліномів будь-якого порядку не залежать від значень самої функції. Таким чином, поліноміальні криві росту можна використовувати для апроксимації (наближення) та прогнозування економічних процесів, в яких подальший розвиток не залежить від досягнутого рівня. Використання експоненційних кривих росту припускає, що подальший розвиток залежить від досягнутого рівня, наприклад, приріст залежить від значення функції. В економіці найчастіше застосовуються два різновиди експоненційних (показових) кривих: проста експонента і модифікована експонента. Проста експонента представляється у вигляді функції
де Ордината даної функції змінюється з постійним темпом приросту. Якщо взяти відношення приросту до самої ординати, воно буде постійною величиною:
Прологарифмуємо вираз для даної функції з будь-якої основою, наприклад
Звідси випливає, що логарифми ординат простої експоненти лінійно залежать від часу. Експоненційна функція може набирати різних чисельних еквівалентних форм:
Усі ці форми використовуються на практиці для опису різних економічних процесів. Наприклад, форму (3) найчастіше використовують у фінансах. В цьому разі Модифікована експонента має вигляд
де постійні величини:
Якщо прологарифмувати перші прирости даної функції, то вийде функція, лінійно залежна від часу, а якщо взяти відношення двох послідовних приростів, воно буде постійною величиною:
Модифікована експонента використовується для опису економічних процесів, які обмежені знизу (рис. 17.1.). Наприклад, таку модель використовують в дослідженнях ринку.
Рис. 17.1. Модифікована експонента При При Наявність параметра В економіці досить поширені процеси, які спочатку зростають повільно, потім прискорюються, а потім знову сповільнюють свій ріст, прямуючи до певної межі. Як приклад можна привести процес введення деякого об’єкта в промислову експлуатацію, процес зміни попиту на товари, що мають здатність досягати певного рівня насичення, і ін. Для моделювання таких процесів використовуються так звані Крива Гомперця має аналітичний вираз:
де
Рис.17.2. Крива Гомперця У кривої Гомперця виділяються чотири ділянки: на першій - приріст функції незначний, на другій - приріст збільшується, на третій ділянці приріст приблизно постійний, на четвертій - відбувається уповільнення темпів приросту і функція необмежено наближається до значення Логарифм даної функції є експоненційною кривою; логарифм відношення першого приросту до самої ординати функції - лінійна функція часу. На підставі кривої Гомперца описується, наприклад, динаміка показників рівня життя; модифікації цієї кривої використовуються в демографії для моделювання показників смертності і т. д. Логістична крива, або крива Перла-Ріда – зростаюча функція, найбільш часто виражається у вигляді:
інші види цієї кривої:
У цих виразах Якщо взяти похідну даної функції, то можна побачити, що швидкість зростання логістичної кривої в кожен момент часу пропорційна досягнутому рівню функції і різниці між граничним значенням і досягнутим рівнем. Логарифм відношення першого приросту функції до квадрату її значення (ординати) є лінійною функцією від часу. Конфігурація графіка логістичної кривої близька до графіку кривої Гомперця, але на відміну від останньої, логістична крива має точку симетрії, що збігається з точкою перегину.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.154.41 (0.013 с.) |
 -подібні криві зростання.
-подібні криві зростання. (поліном першого ступеня)
(поліном першого ступеня)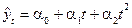 (поліном другого ступеня)
(поліном другого ступеня) (поліном третього ступеня) і т.д.
(поліном третього ступеня) і т.д. називають лінійним приростом, параметр
називають лінійним приростом, параметр  – прискоренням зростання, параметр
– прискоренням зростання, параметр  – зміною прискорення зростання.
– зміною прискорення зростання. , вони будуть постійними рівними величинами.
, вони будуть постійними рівними величинами. на графіку буде представлений прямою лінією. Другі прирости
на графіку буде представлений прямою лінією. Другі прирости  i для полінома другого степеня будуть постійні.
i для полінома другого степеня будуть постійні. , будуть постійними величинами.
, будуть постійними величинами. (17.1)
(17.1)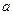 і
і  – позитивні числа, при цьому якщо
– позитивні числа, при цьому якщо  (17.2)
(17.2) :
: (17.3)
(17.3) , основна форма
, основна форма 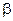 >0; (1)
>0; (1) ,
,  , де
, де 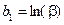 ; (2)
; (2)
 , де
, де  ; (3)
; (3) замінюємо на
замінюємо на  та
та  і
і  ; (4)
; (4)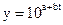 ,
,  замінюємо на
замінюємо на  і
і  , де
, де  ,
,  . (5)
. (5) інтерпретується як норма річного відсотка.
інтерпретується як норма річного відсотка. (17.4)
(17.4) називається асимптотою цієї функції, тобто значення функції необмежено наближаються (знизу) до величини
називається асимптотою цієї функції, тобто значення функції необмежено наближаються (знизу) до величини  (17.5)
(17.5)
 модифікована експонента спочатку повільно, а потім швидко зростає і обмежена знизу прямою
модифікована експонента спочатку повільно, а потім швидко зростає і обмежена знизу прямою  .
. модифікована експонента спадає і також обмежена знизу значенням
модифікована експонента спадає і також обмежена знизу значенням  .
. . Для обчислення невідомих параметрів, в даному випадку, необхідно застосовувати методи нелінійного оцінювання.
. Для обчислення невідомих параметрів, в даному випадку, необхідно застосовувати методи нелінійного оцінювання. , (17.6)
, (17.6)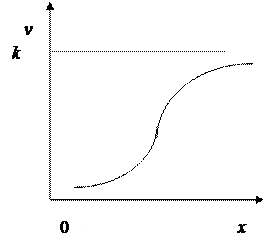
 (17.7)
(17.7) ,
,  (17.8)
(17.8)


