
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оцінка адекватності і точності трендових моделей.
Незалежно від виду і способу побудови економіко-математичної моделі питання про можливість її застосування з метою аналізу та прогнозування економічного явища може бути вирішене тільки після встановлення адекватності, тобто відповідності моделі досліджуваному процесу або об’єкту. Так як повної відповідності моделі реальному процесу або об’єкту бути не може, адекватність - певною мірою умовне поняття. При моделюванні мається на увазі адекватність не взагалі, а за тими властивостями моделі, які вважаються суттєвими для дослідження. Трендова модель Перевірка випадковості коливань рівнів залишкової послідовності означає перевірку гіпотези про правильність вибору виду тренду. Для дослідження випадковості відхилень від тренда розглядають різниці:
Характер цих відхилень вивчається за допомогою ряду непараметричних критеріїв. Одним з таких критеріїв є критерій серій, заснований на медіані вибірки. Ряд з величин Позначимо число знаків найдовшої серії через
де Якщо хоча б одна з цих умов не виконується, то гіпотеза про випадковий характер відхилень рівнів часового ряду від тренду відхиляється і трендова модель визнається неадекватною.
Іншим критерієм для даної умови може служити критерій піків (поворотних точок). Рівень послідовності В випадковій вибірці математичне сподівання числа точок повороту
Критерієм випадковості з 5%-вим рівнем значимості, тобто з довірчою ймовірністю 95%, є виконання умови:
де Якщо умова не виконується, трендова модель вважається неадекватною. Перевірка відповідності розподілу випадкової компоненти нормальному закону розподілу може бути проведена лише приблизно за допомогою дослідження показників асиметрії
У цих формулах Якщо одночасно виконуються наступні умови:
то гіпотеза про нормальний характер розподілу випадкової компоненти приймається. Якщо виконується хоча б одна з умов:
то гіпотеза про нормальний характер розподілу відхиляється, трендова модель визнається неадекватною. Інші випадки потребують додаткової перевірки за допомогою більш складних критеріїв. Крім розглянутого методу відомий ряд інших методів перевірки нормальності закону розподілу випадкової величини: метод Вестергарда, У нашому випадку
Для ілюстрації наведемо кілька пар значень критичних меж Перевірка рівності математичного сподівання випадкової компоненти нулю, якщо вона розподілена за нормальним законом, здійснюється на основі
де Якщо розрахункове значення Перевірка незалежності значень рівнів випадкової компоненти, тобто перевірка відсутності істотної автокореляції в залишковій послідовності може здійснюватися за рядом критеріїв, найбільш поширеним з яких є Зауважимо, що розрахункове значення критерію Дарбіна-Уотсона в інтервалі від 2 до 4 свідчить про обернений зв’язок; в цьому випадку його треба перетворити за формулою Якщо розрахункове значення критерію Висновок про адекватність трендової моделі робиться, коли всі вказані вище чотири перевірки властивостей залишкової послідовності дають позитивний результат. Для адекватних моделей має сенс ставити задачу оцінки їх точності. Точність моделі характеризується величиною відхилення виходу моделі від реального значення модельованої змінної (економічного показника). Для показника, представленого тимчасовим рядом, точність визначається як різниця між значенням фактичного рівня часового ряду і його оцінкою, отриманою розрахунковим шляхом з використанням моделі, при цьому в якості статистичних показників точності застосовуються наступні: – середнє квадратичне відхилення – середня відносна помилка апроксимації – коефіцієнт збіжності – коефіцієнт детермінації в наведених формулах На підставі зазначених показників можна зробити вибір з декількох адекватних трендових моделей економічної динаміки найбільш точну, хоча може зустрітися випадок, коли за деяким показником більш точна одна модель, а за іншим – інша.
Дані показники точності моделей розраховуються на основі всіх рівнів часового ряду і тому відбивають лише точність апроксимації. Для оцінки прогнозних властивостей моделі доцільно використовувати так званий ретроспективний прогноз – підхід, заснований на виділенні ділянки з ряду останніх рівнів вихідного часового ряду в кількості, наприклад,
де Оцінювання прогнозних властивостей моделі на ретроспективній ділянці дуже корисно, особливо при зіставленні різних моделей прогнозування з числа адекватних. Однак треба пам’ятати, що оцінки ретропрогнозу – лише наближена міра точності прогнозу і моделі в цілому, так як прогноз на період випередження виконується за моделлю, побудованою за всіма рівнями ряду.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.168 (0.012 с.) |
 конкретного часового ряду
конкретного часового ряду  вважається адекватною, якщо правильно відображає систематичні компоненти тимчасового ряду. Ця вимога еквівалентна вимозі, щоб залишкова компонента
вважається адекватною, якщо правильно відображає систематичні компоненти тимчасового ряду. Ця вимога еквівалентна вимозі, щоб залишкова компонента  задовольняла властивостям випадкової компоненти часового ряду, розглянутим в п. 12.1.
задовольняла властивостям випадкової компоненти часового ряду, розглянутим в п. 12.1. ранжують за зростанням їх значень і знаходять медіану
ранжують за зростанням їх значень і знаходять медіану  отриманого варіаційного ряду. Повертаючись до вихідної послідовності
отриманого варіаційного ряду. Повертаючись до вихідної послідовності  . Послідовність послідовних плюсів чи мінусів називається серією. Для того щоб послідовність
. Послідовність послідовних плюсів чи мінусів називається серією. Для того щоб послідовність  , а загальне число серій - через
, а загальне число серій - через  . Вибірка визнається випадковою, якщо виконуються наступні умови для 5%-вого рівня значимості:
. Вибірка визнається випадковою, якщо виконуються наступні умови для 5%-вого рівня значимості: (17.12)
(17.12)
 – ціла частина числа.
– ціла частина числа. , і мінімумом, якщо він менше обох сусідніх рівнів, т. т.
, і мінімумом, якщо він менше обох сусідніх рівнів, т. т.  . В обох випадках
. В обох випадках 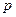 .
. і дисперсія
і дисперсія  виражаються формулами:
виражаються формулами: ;
; 
 (17.13)
(17.13) та ексцесу
та ексцесу  , так як часові ряди, як правило, не дуже великі. При нормальному розподілі показники асиметрії та ексцесу деякої генеральної сукупності дорівнюють нулю. Ми припускаємо, що відхилення від тренду являють собою вибірку з генеральної сукупності, тому можна визначити тільки вибіркові характеристики асиметрії та ексцесу і їхні помилки:
, так як часові ряди, як правило, не дуже великі. При нормальному розподілі показники асиметрії та ексцесу деякої генеральної сукупності дорівнюють нулю. Ми припускаємо, що відхилення від тренду являють собою вибірку з генеральної сукупності, тому можна визначити тільки вибіркові характеристики асиметрії та ексцесу і їхні помилки: ;
;  ;
;  ;
;  (17.14)
(17.14) – вибіркова характеристика асиметрії;
– вибіркова характеристика асиметрії;  – вибіркова характеристика ексцесу;
– вибіркова характеристика ексцесу;  та
та  - відповідні середньоквадратичні помилки.
- відповідні середньоквадратичні помилки. ;
; 
 ;
; 
 -критерій і т. д. Розглянемо найбільш простий з них, заснований на
-критерій і т. д. Розглянемо найбільш простий з них, заснований на  до стандартного відхилення
до стандартного відхилення  .
. , a
, a  . Обчислення значення
. Обчислення значення  : при
: при 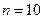 нижня межа дорівнює 2,67, а верхня дорівнює 3,685; при
нижня межа дорівнює 2,67, а верхня дорівнює 3,685; при  ці числа становлять відповідно 3,18 і 4,49; при
ці числа становлять відповідно 3,18 і 4,49; при  вони рівні 3,47 і 4,89.
вони рівні 3,47 і 4,89. -критерію Стьюдента. Розрахункове значення цього критерію задається формулою:
-критерію Стьюдента. Розрахункове значення цього критерію задається формулою: (17.15)
(17.15) – середнє арифметичне значення рівнів залишкової послідовності
– середнє арифметичне значення рівнів залишкової послідовності  – стандартне (середньоквадратичне) відхилення для цієї послідовності.
– стандартне (середньоквадратичне) відхилення для цієї послідовності. статистики Стьюдента з заданим рівнем значимості
статистики Стьюдента з заданим рівнем значимості  і числом ступенів свободи
і числом ступенів свободи  , то гіпотеза про рівність нулю математичного сподівання випадкової послідовності приймається; в іншому випадку ця гіпотеза відхиляється і модель вважається неадекватною.
, то гіпотеза про рівність нулю математичного сподівання випадкової послідовності приймається; в іншому випадку ця гіпотеза відхиляється і модель вважається неадекватною. -критерій Дарбіна-Уотсона (див. п. 7.3.).
-критерій Дарбіна-Уотсона (див. п. 7.3.). і надалі використовувати значення
і надалі використовувати значення  .
.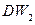 , то гіпотеза про незалежність рівнів залишкової послідовності, тобто про відсутність у ній автокореляції, приймається. Якщо значення
, то гіпотеза про незалежність рівнів залишкової послідовності, тобто про відсутність у ній автокореляції, приймається. Якщо значення 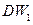 ,то ця гіпотеза відхиляється і модель неадекватна. Якщо значення
,то ця гіпотеза відхиляється і модель неадекватна. Якщо значення  (17.16)
(17.16) (17.17)
(17.17) (17.18)
(17.18) (5.16)
(5.16) – кількість рівнів ряду,
– кількість рівнів ряду,  – число параметрів, моделі;
– число параметрів, моделі;  – середнє арифметичне значення рівнів ряду.
– середнє арифметичне значення рівнів ряду. рівнів в якості перевірочних, а саму трендову модель в цьому випадку слід будувати за першими точками, кількість яких дорівнюватиме
рівнів в якості перевірочних, а саму трендову модель в цьому випадку слід будувати за першими точками, кількість яких дорівнюватиме  . Тоді для розрахунку показників точності моделі за ретроспективним прогнозом застосовуються ті ж формули, але підсумовування в них буде вестися не за всіма спостереженнями, а лише за останніми
. Тоді для розрахунку показників точності моделі за ретроспективним прогнозом застосовуються ті ж формули, але підсумовування в них буде вестися не за всіма спостереженнями, а лише за останніми 
 рівнів.
рівнів.


