
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблема ототожнення в симультативних моделях
Як уже зазначалося, в симультативній моделі є змінні двох типів: ендогенні та попередньо визначені. Ендогенні змінні вважаються стохастичними, тоді як попередньо визначені змінні трактуються як не стохастичні. Попередньо визначені змінні поділяються на дві категорії: поточні та лагові. Так, наприклад, якщо Зауважимо, що не всі змінні обов’язково мають з’являтись у кожному рівнянні. З симультативної (структурної) моделі, як ми вже розглядали вище, можна отримати скорочену форму, в якій ендогенні змінні залежать тільки від попередньо визначених змінних та випадкових величин. Під проблемою оцінювання параметрів симультативних моделей розуміють знаходження оцінок параметрів на основі оцінених коефіцієнтів скороченої форми. Якщо це можна зробити, то ми маємо право стверджувати, що модель ототожнена. І навпаки. Ототожнена модель може бути як точно ототожненою, так і переототожненою. Точно ототожнену модель ми маємо в тому разі, коли можна отримати однозначну оцінку її параметрів. Переототожнену модель ми маємо у разі, коли для деяких параметрів структурної моделі є можливість отримати більше ніж одне кількісне значення. Крім того, модель може бути і неототожненою. Розрахунок параметрів системи економетричних рівнянь попиту та пропозиції непрямим методом найменших квадратів. Основні правила ототожнення Розглянемо основні правила ототожнення симультативних моделей. Введемо таку систему позначень:
З врахуванням введеної системи позначень сформулюємо обов’язкову (але не достатню) умову ототожнення, яка має назву «умова порядку» і може бути визначена двома різними, але еквівалентними способами.
Визначення 1. Для ототожнення рівняння в ньому має бути опущено щонайменше Визначення 2. Для ототожнення рівняння число попередньо визначених змінних, опущених в ньому, має бути не меншим за число включених в нього ендогенних змінних мінус одиниця, тобто Якщо Щоб проілюструвати умову порядку, звернемось до попередніх прикладів. Приклад 1 Функція попиту: Функція пропозиції:
Приклад 2 Функція попиту: Функція пропозиції: У даній моделі Застосовуючи умову порядку, бачимо, що функція попиту неототожнена. З іншого боку, функція пропозиції ототожнена, бо в ній опущено рівно одну змінну Приклад 3 Функція попиту: Функція пропозиції: У даній моделі Приклад 4 Функція попиту: Функція пропозиції: У даній моделі Як показують попередні приклади, ототожнення рівнянь симультативних моделей можливе тоді, коли в окремих рівняннях опущено одну чи більше змінних, які є ще де-небудь у моделі. Рангова умова ототожнення Умова порядку, яка обговорювалась раніше, є обов’язковою, але не достатньою умовою ототожнення. Тобто може статися так, що навіть якщо умова порядку
Рангова умова ототожнення: в симультативній моделі, яка містить Алгоритм перевірки рівняння за ранговою умовою: 1. Записати систему симультативних рівнянь у табличній формі. 2. Викреслити коефіцієнти рядка, в якому з’являється рівняння, що розглядається. 3. Викреслити стовпці, відповідні ненульовим коефіцієнтам, рівняння, що розглядається. 4. Отримаємо необхідну матрицю. Якщо ранг матриці точно дорівнює На базі умов порядку та рангу можна сформулювати загальні принципи ототожнення структурного рівняння в моделі, яка складається з 1. Якщо 2. Якщо 3. Якщо 4. Якщо Тема 15. ННК. 2МНК. Рекурсивні системи одночасних рівнянь 1. Двокроковий метод найменших квадратів оцінки параметрів надідентифікованої системи одночасних рівнянь, узагальнений алгоритм методу. 2. Двокроковий метод найменших квадратів і головних компонентів. 3. Сфера застосування їх в економетричних дослідженнях. 4. Рекурсивні системи одночасних рівнянь, їх характеристика, можливість застосування МНК-оцінки для розрахунку параметрів рекурсивних систем. 5. Приклади макромоделей. 6. Прогнози.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.01 с.) |
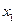 є поточною екзогенною змінною, то
є поточною екзогенною змінною, то 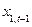 вважається лаговою екзогенною змінною з одиничним лагом. Якщо
вважається лаговою екзогенною змінною з одиничним лагом. Якщо 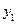 є ендогенною змінною, то
є ендогенною змінною, то  – лагова змінна, значення якої відоме в поточний період часу
– лагова змінна, значення якої відоме в поточний період часу  , отже це значення вважається не стохастичним, а
, отже це значення вважається не стохастичним, а  є також попередньо визначеною змінною. Право визначати, які змінні ендогенні, а які попередньо визначені, належить досліднику, котрий розробляє модель.
є також попередньо визначеною змінною. Право визначати, які змінні ендогенні, а які попередньо визначені, належить досліднику, котрий розробляє модель.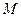 - кількість ендогенних змінних у симультативній моделі;
- кількість ендогенних змінних у симультативній моделі; - кількість ендогенних змінних у окремому рівнянні;
- кількість ендогенних змінних у окремому рівнянні;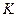 - кількість попередньо визначених змінних у моделі;
- кількість попередньо визначених змінних у моделі; - кількість попередньо визначених змінних у окремому рівнянні.
- кількість попередньо визначених змінних у окремому рівнянні.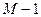 змінних, які з’являються в цілому в моделі. Якщо опущено рівно
змінних, які з’являються в цілому в моделі. Якщо опущено рівно 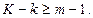
 , рівняння точно ототожнене, але якщо
, рівняння точно ототожнене, але якщо 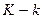 >
> 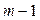 , воно переототожнене.
, воно переототожнене.

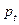 – ціна. Ця модель має дві ендогенні змінні
– ціна. Ця модель має дві ендогенні змінні  і жодної попередньо визначеної. Для ототожнення в кожному рівнянні має бути опущена щонайменше змінна. В даному разі жодне з рівнянь не буде ототожненим.
і жодної попередньо визначеної. Для ототожнення в кожному рівнянні має бути опущена щонайменше змінна. В даному разі жодне з рівнянь не буде ототожненим.

 – екзогенна.
– екзогенна.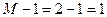 ).
).
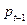 – екзогенні змінні. У першому рівнянні опущено рівно одну змінну
– екзогенні змінні. У першому рівнянні опущено рівно одну змінну 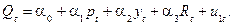

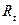 – екзогенні змінні. У функції попиту опущено рівно одну змінну
– екзогенні змінні. У функції попиту опущено рівно одну змінну  .
. виконана, рівняння може бути неототожненим, тому що попередньо визначені змінні, які опущено в ньому, але є в моделі, можуть бути залежними. Через це відповідність між структурними коефіцієнтами (
виконана, рівняння може бути неототожненим, тому що попередньо визначені змінні, які опущено в ньому, але є в моделі, можуть бути залежними. Через це відповідність між структурними коефіцієнтами (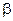 ) і коефіцієнтами скороченої форми (
) і коефіцієнтами скороченої форми ( ) не зберігається. Тобто ми не можемо оцінити структурні параметри за коефіцієнтами скороченої форми. Тому потрібно мати як достатню, так і необхідну умову ототожнення. Такою умовою є рангова умова ототожнення, яка формулюється таким чином.
) не зберігається. Тобто ми не можемо оцінити структурні параметри за коефіцієнтами скороченої форми. Тому потрібно мати як достатню, так і необхідну умову ототожнення. Такою умовою є рангова умова ототожнення, яка формулюється таким чином.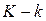 >
> 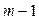 і ранг матриці буде дорівнювати
і ранг матриці буде дорівнювати 


