
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила и формулы интегрированияСодержание книги
Поиск на нашем сайте
РГР № 3 Вариант № 1 1.Найдите неопределенные интегралы.
a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной параболой 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по кривой c) по окружности
РГР № 3 Вариант № 2
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите длину дуги кривой 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по окружности
РГР № 3 Вариант № 3
1.Найдите неопределенные интегралы.
a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по эллипсу
РГР № 3 Вариант № 4
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной линией 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по окружности
РГР № 3 Вариант № 5 1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите длину дуги арки циклоиды 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по параболе
РГР № 3 Вариант № 6
1.Найдите неопределенные интегралы. a) b) c) d) e)
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболой 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по параболе
РГР № 3 Вариант № 7
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите длину дуги кривой 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по эллипсу
РГР № 3 Вариант № 8
1.Найдите неопределенные интегралы.
a) b) c) d) e)
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной линиями 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по гиперболе c) по прямой
РГР № 3 Вариант № 9
1.Найдите неопределенные интегралы. a) b) c) d) e)
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите длину дуги полукубической параболы 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по эллипсу
РГР № 3 Вариант № 10
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной линией 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по параболе c) по эллипсу
РГР № 3 Вариант № 11
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линией 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по параболе
РГР № 3 Вариант № 12
1.Найдите неопределенные интегралы. a) b) c) d) e)
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите длину дуги полукубической параболы 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по параболе c) по прямой
РГР № 3 Вариант № 13
1.Найдите неопределенные интегралы.
РГР № 3 Вариант № 14
1.Найдите неопределенные интегралы.
РГР № 3 Вариант № 15
1.Найдите неопределенные интегралы. a) b) c) d) e)
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной одной аркой циклоиды
5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по кривой c) по прямой x = t−3; y=t
РГР № 3 Вариант № 16
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривыми 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по окружности
РГР № 3 Вариант № 17
1.Найдите неопределенные интегралы.
РГР № 3 Вариант № 18
1.Найдите неопределенные интегралы. a) b) c) d) e)
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболами 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по кривой c) по прямой
РГР № 3 Вариант № 19
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной параболой 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по параболе
РГР № 3 Вариант № 20
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите длину астроиды 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по параболе c) по прямой
РГР № 3 Вариант № 21
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной четырехлепестковой розой 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по гиперболе c) по прямой
РГР № 3 Вариант № 22
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите длину дуги кривой 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по окружности
РГР № 3 Вариант № 23
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите площадь фигуры, ограниченной линиями 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по полукубической параболе
РГР № 3 Вариант № 24
1.Найдите неопределенные интегралы. a) b) c) d) e) 2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
3. Вычислите несобственные интегралы или докажите их расходимость.
4. Произвести вычисления. Вычислите объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной кривыми 5. В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
6. Вычислите криволинейный интеграл
a) по прямой c) по параболе
РГР № 3 Вариант № 25
1.Найдите неопределенные интегралы. a) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 ;
; ;
; ;
; ;
; .
. ;
;
 и прямой
и прямой  .
. ;
;
 .
.
 , где L — путь, соединяющий точки О (0, 0) и А (1, 1)
, где L — путь, соединяющий точки О (0, 0) и А (1, 1) ; b) по ломаной линии ОВА, где В (0, 1);
; b) по ломаной линии ОВА, где В (0, 1); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (1, 0) и В (0, 1)
, где L — путь, соединяющий точки А (1, 0) и В (0, 1) ; b) по ломаной линии АСВ, где С (1, 1);
; b) по ломаной линии АСВ, где С (1, 1); .
. ;
; ;
; ;
; ;
; .
.

 ,x=1.
,x=1. ;
;
 .
.
 , где L — путь, соединяющий точки О (0, 0) и А (–4, 2)
, где L — путь, соединяющий точки О (0, 0) и А (–4, 2) ; b) по ломаной линии ОCА, где C (0, 2);
; b) по ломаной линии ОCА, где C (0, 2); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (–2, 0) и В (0, 2)
, где L — путь, соединяющий точки А (–2, 0) и В (0, 2) ; b) по ломаной линии АСВ, где С (–2, 2);
; b) по ломаной линии АСВ, где С (–2, 2); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (0, –3) и В (3, 0)
, где L — путь, соединяющий точки А (0, –3) и В (3, 0) ; b) по ломаной линии АСВ, где С (3, –3);
; b) по ломаной линии АСВ, где С (3, –3); .
. ;
; ;
; ;
; ;
; .
.

 и прямой
и прямой  .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (–1, 0) и В (0, –1)
, где L — путь, соединяющий точки А (–1, 0) и В (0, –1) ; b) по ломаной линии АСВ, где С (–1,–1);
; b) по ломаной линии АСВ, где С (–1,–1); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (2, 0) и В (0, 4)
, где L — путь, соединяющий точки А (2, 0) и В (0, 4) ; b) по ломаной линии АСВ, где С (2, 4);
; b) по ломаной линии АСВ, где С (2, 4); .
. ;
; ;
; ;
; ;
; .
.


 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А
, где L — путь, соединяющий точки А  и В
и В 
 ; b) по ломаной линии АСВ, где С (2, 2);
; b) по ломаной линии АСВ, где С (2, 2); .
. ;
; ;
; ;
; ;
; .
.
 от точки
от точки  до точки
до точки  .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (–1, 0) и В (0, 2)
, где L — путь, соединяющий точки А (–1, 0) и В (0, 2) ; b) по ломаной линии АСВ, где С (–1, 2);
; b) по ломаной линии АСВ, где С (–1, 2); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (4, 0) и В (0, 2)
, где L — путь, соединяющий точки А (4, 0) и В (0, 2) ; b) по ломаной линии АСВ, где С (4, 2);
; b) по ломаной линии АСВ, где С (4, 2); .
. ;
; ;
; ;
; ;
; .
.
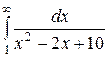
 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (1, 2) и В (2, 1)
, где L — путь, соединяющий точки А (1, 2) и В (2, 1) .
. ;
; ;
; ;
; ;
; .
.
 от точки
от точки  до точки
до точки  .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (9, 0) и В (0, 3)
, где L — путь, соединяющий точки А (9, 0) и В (0, 3) ; b) по ломаной линии АСВ, где С (9, 3);
; b) по ломаной линии АСВ, где С (9, 3); .
. ;
b)
;
b) 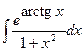 ;
c)
;
c)  ;
d)
;
d)  ;
e)
;
e)  .
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
.
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
 3. Вычислите несобственные интегралы или докажите их расходимость.
3. Вычислите несобственные интегралы или докажите их расходимость.
 4.Произвести вычисления.
Вычислите площадь фигуры, ограниченной кардиоидой
4.Произвести вычисления.
Вычислите площадь фигуры, ограниченной кардиоидой  .
5.В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
.
5.В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
 ;
;
 .
.
 , где L — путь, соединяющий точки А (–1, 0) и В (0, –1)
, где L — путь, соединяющий точки А (–1, 0) и В (0, –1) .
. ;
b)
;
b)  ;
c)
;
c)  ;
d)
;
d)  e)
e)  .
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
.
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
 3. Вычислите несобственные интегралы или докажите их расходимость.
3. Вычислите несобственные интегралы или докажите их расходимость.
 4.Произвести вычисления.
Вычислите площадь фигуры, ограниченной линиями
4.Произвести вычисления.
Вычислите площадь фигуры, ограниченной линиями  и
и  .
5.В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
.
5.В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
 ;
;
 .
.
 , где L — путь, соединяющий точки А (–1, 0) и В (0, 2)
, где L — путь, соединяющий точки А (–1, 0) и В (0, 2) ;
; ;
; ;
; ;
; .
.

 и осью Ох.
и осью Ох. ;
;
 .
.
 , где L — путь, соединяющий точки А (0, 3) и В (1, 4)
, где L — путь, соединяющий точки А (0, 3) и В (1, 4) ; b) по ломаной линии АСВ, где С (0, 4);
; b) по ломаной линии АСВ, где С (0, 4); ;
;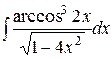 ;
; ;
;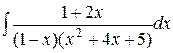 ;
; .
.

 и осью Оу
и осью Оу 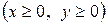 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (3,0) и В (0, 3)
, где L — путь, соединяющий точки А (3,0) и В (0, 3) .
. ;
b)
;
b)  ;
c)
;
c)  ;
d)
;
d)  ;
e)
;
e)  .
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
.
2. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
 3. Вычислите несобственные интегралы или докажите их расходимость.
3. Вычислите несобственные интегралы или докажите их расходимость.
 4.Произвести вычисления.
Вычислите длину дуги кардиоиды
4.Произвести вычисления.
Вычислите длину дуги кардиоиды  .
5.В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
.
5.В двойном интеграле расставьте пределы интегрирования двумя способами (меняя порядок интегрирования) и вычислите интеграл.
 ;
;
 .
.
 , где L — путь, соединяющий точки А (2, 0) и В (3, 1)
, где L — путь, соединяющий точки А (2, 0) и В (3, 1) ; b) по ломаной линии АСВ, где С (2, 1);
; b) по ломаной линии АСВ, где С (2, 1); .
.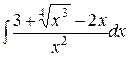 ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А
, где L — путь, соединяющий точки А  и В
и В 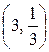
 ;
; .
. ;
; ;
; ;
; ;
; .
.

 и прямой
и прямой  .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (0, 2) и В (1, 3)
, где L — путь, соединяющий точки А (0, 2) и В (1, 3) ; b) по ломаной линии АСВ, где С (0, 3);
; b) по ломаной линии АСВ, где С (0, 3); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (–4, 0) и В (0, –2)
, где L — путь, соединяющий точки А (–4, 0) и В (0, –2) ; b) по ломаной линии АСВ, где С (–4, –2);
; b) по ломаной линии АСВ, где С (–4, –2);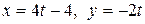 .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А
, где L — путь, соединяющий точки А  и В
и В 
 ;
; .
. ;
; ;
;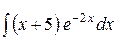 ;
; ;
; .
.

 , ограниченной прямыми
, ограниченной прямыми  .
. ;
;
 .
.
 , где L — путь, соединяющий точки O (0, 0) и В (2, 2)
, где L — путь, соединяющий точки O (0, 0) и В (2, 2) ; b) по ломаной линии OСВ, где С (0, 2);
; b) по ломаной линии OСВ, где С (0, 2); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки О (0, 0) и А
, где L — путь, соединяющий точки О (0, 0) и А 
 ; b) по ломаной линии ОВА, где В (–1, 0);
; b) по ломаной линии ОВА, где В (–1, 0); .
. ;
; ;
; ;
; ;
; .
.

 .
. ;
;
 .
.
 , где L — путь, соединяющий точки А (–2, 5) и В (0, 1)
, где L — путь, соединяющий точки А (–2, 5) и В (0, 1) ; b) по ломаной линии АСВ, где С (0, 5);
; b) по ломаной линии АСВ, где С (0, 5); .
.


