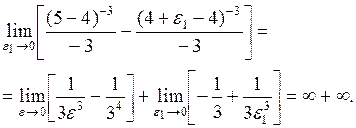Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непосредственное интегрирование ⇐ ПредыдущаяСтр 2 из 2
Пример 1. Найти интеграл Решение. Преобразуем подынтегральное выражение и воспользуемся формулами 1, 2, 4. Получим
Здесь мы применили известные формулы
Проверим найденный результат дифференцированием. Найдем
что совпадает с подынтегральным выражением, и, следовательно, интегрирование проведено правильно.
МЕТОД ПОДСТАНОВКИ ИЛИ ЗАМЕНЫ ПЕРЕМЕННОЙ Пример 2. Вычислить интеграл Решение. Сделаем подстановку
Из подстановки Таким образом, мы получили табличный интеграл
Пример 3. Вычислить интеграл Решение. Сделаем подстановку
Возвращаясь к переменной Сделаем проверку Аналогичным образом вычислим еще несколько интегралов, не делая подробных объяснений.
Пример 4.
Пример 5. Пример 6.
Пример 8.
МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ Пример 9. Вычислить интеграл Решение. Обозначим
Пример 10. Вычислить интеграл Решение.
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ Пример 11. Вычислить интеграл Решение. Представим подынтегральную дробь в виде суммы простейших дробей. Так как квадратный трехчлен
Отсюда получаем
или или Приравнивая коэффициенты при одинаковых степенях
Таким образом,
ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ Пример 12. Вычислить интеграл Решение. Так как Разделив
Следовательно,
ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Пример 13. Вычислить интеграл Решение.
Пример 14. Вычислить интеграл Решение.
Пример 15. Вычислить интеграл Решение. Применим универсальную подстановку
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Пример 16. Вычислить определенный интеграл
Решение.
При вычислении этого интеграла были применены формулы
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ Несобственные интегралы по бесконечному промежутку
Пример 17. Вычислить несобственный интеграл Решение.
Таким образом, несобственный интеграл равен
Несобственные интегралы второго рода Пример 18. Вычислить интеграл
Решение.
Так как оба предела стремятся к бесконечности, то они не существуют и поэтому, несобственный интеграл расходится (рис. 1).
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.70.9 (0.011 с.) |

 .
. и
и  . Следовательно,
. Следовательно,
 .
.
 ,
,
 , тогда
, тогда  и
и  . Поэтому интеграл преобразуется к виду
. Поэтому интеграл преобразуется к виду .
. и
и 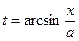 . Тогда
. Тогда  .
. .
.
 . Тогда
. Тогда 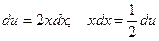 . Переходя под интегралом к переменной
. Переходя под интегралом к переменной 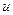 , получим
, получим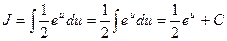 .
. , найдем окончательно
, найдем окончательно  .
. , что совпадает с подынтегральным выражением.
, что совпадает с подынтегральным выражением.

 .
. .
.


 . Тогда
. Тогда 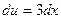 , а
, а 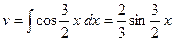 (см. пример 7, формулу (3)) Получим
(см. пример 7, формулу (3)) Получим
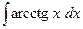

 (см. пример 4).
(см. пример 4).
 имеет отрицательный дискриминант
имеет отрицательный дискриминант 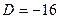 , то
, то
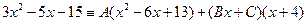 ,
, ,
,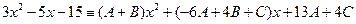 .
.


 .
.
 , сделаем подстановку
, сделаем подстановку  . Тогда
. Тогда  и
и  .
. на
на  , получим
, получим , где
, где  .
.




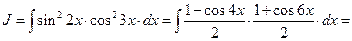


 .
.






 или доказать его расходимость
или доказать его расходимость
 , т. е. он сходится.
, т. е. он сходится. или доказать его расходимость.
или доказать его расходимость.