
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамічна механічна та електромеханічна характеристика двигуна з незалежним збудженнямСодержание книги
Поиск на нашем сайте
Динамічна механічна та електромеханічна характеристика – це залежності w=f(M) таw=f(I) для всіх режимів роботи двигуна, як для статичного, так і для динамічного. Рівняння динамічних характеристик отримуються аналогічно до статичних характеристик, але не основі статичного рівняння (2.3), а на базі диференціального рівняння (2.36) кола якоря
Після підстановки у (2.49) відомого виразу для ЕРС двигуна E = cФw
знаходиться рівняння динамічної електромеханічної характеристики
w= – –. (2.50)
Якщо до (2.50) підставити значення струму якоря з виразу для моменту I=, то отримується рівняння динамічної механічної характеристики
w = – M – (2.51) або w = w0 +
де w0= – швидкість ідеального холостого ходу; b= – статична жорсткість механічної характеристики.
Динамічна механічна характеристика (2.52) характеризується динамічною жорсткістю, яка являє собою передаточну функцію ЕМП за збуренням bдин(р) = = –, (2.53)
та зсувом фаз між моментом та швидкістю
Dy(р) = yМ – yw, (2.54)
що, отримуються на основі структурної схеми на рис. 2.47. У статичному режимі, тобто при р=0, модуль динамічної жорсткості дорівнює статичній жорсткості характеристики, взятої з протилежним знаком, |bдин(р)| = –b = –,
а зсув фаз дорівнює Dy(р) = –p. Випадок усталеного динамічного режиму роботи двигуна розглядається при дії статичного моменту з періодичною складовою
Mс = M = Mсер + DМmaxsinWt. (2.55)
Після підстановки моменту (2.55) у рівняння динамічної механічної характеристики (2.52) отримується закон зміни швидкості двигуна при дії періодичного статичного моменту
w= – sinWt – cosWt = = wсер –
де y =-p-arctg(WТя) – фаза; Мкз=bw0 – момент короткого замикання.
Згідно (2.56) динамічна характеристика представляє собою замкнену криву у вигляді еліпса, що видно з рис. 2.53.
Рис. 2.53.
Величина коливань швидкості Dw збільшується при збільшенні Тя, W, DМmax та зменшенні жорсткості b. Зсув фаз змінюється від –1800 при Тя=0 чи W=0 і до –2700 при збільшенні Тя та при W®¥. Динамічна механічна характеристика зливається зі статичною при Тя=0 чи W=0. Як видно з рис. 2.53, динамічна характеристика суттєво відрізняється від статичної, тому при періодичній зміні статичного моменту чи зміні його стрибком потрібно використовувати динамічну механічну характеристику або проводити моделювання електромеханічної системи. Статичні механічні характеристики можна використовувати при постійному значенні статичного моменту або при його повільній зміні відносно електромагнітної сталої часу Тя.
Література: [1, с. 98, 104-105], [2, с. 99-101, 128-131].
СРС: Типові структурні схеми двигуна з незалежним збудженням. Література: [1, с. 98], [5, с. 202-208].
Контрольні запитання: 1. Чим визначається електромагнітна стала часу кола якоря. 2. Чим визначається електромагнітна стала часу кола збудження. 3. Чим визначається електромеханічна стала часу двигуна. 4. Якою типовою ланкою описується коло якоря. 5. Якою типовою ланкою описується коло збудження. 6. Який взаємнозв'язок між колом збудження та якоря. 7. Що таке внутрішній електромеханічний зв'язок двигуна. 8. Який вигляд мають механічні характеристики двигуна при живленні від джерела струму. 9. Чим відрізняється рівняння динамічної механічної характеристики від статичної. 10. У яких випадках слід користуватися статичною чи динамічною механічною характеристикою.
ЛЕКЦІЯ 12
2.1.2. Електромеханічні властивості двигуна постійного струму з послідовним збудженням
У ДПС з послідовним збудженням струм збудження є одночасно струмом якоря (Рис. 2.54), тому магнітний потік залежить від навантаження.
Рис. 2.54.
Перевантажувальна здатність двигуна з послідовним збудженням вища, ніж у двигуна з незалежним збудженням, бо із збільшенням навантаження зростає магнітний потік і відповідно момент двигуна. Так перевантаженню за струмом lІ=2¸3 відповідає перевантаження за моментом lМ = 2,5¸3,5. В загальному випадку рівняння електромеханічної характеристики двигуна з послідовним збудженням співпадає з аналогічним рівнянням двигуна постійного струму з незалежним збудженням (2.6), але магнітний потік є функцією струму якоря Ф=f(I)
w= – І. (2.57)
Для полегшення аналізу реальна крива намагнічування двигуна замінюється двома прямими (Рис. 2.55).
Рис. 2.55.
Для цього в початку координат проводиться дотична до перетинання з прямою, яка проходить на рівні потоку насичення Фнас паралельно осі абсцис. Точка перетину визначає струм межі Ім, який розділяє криву намагнічування на дві ділянки І та ІІ. На першій ділянці при струмі двигуна менше струму межі І£Ім магнітний потік пропорційний струму якоря
Ф=КзІ, (2.58)
де Кз=tga - коефіцієнт кола збудження;
а на другій ділянці, коли І>Ім, магнітний потік незмінний і дорівнює потоку насичення Ф=Фнас=const (2.59)
1) Після підстановки у (2.57) виразу для потоку (2.58) отримується рівняння електромеханічної характеристики при роботі зі струмом якоря меншим за струм межі І£ Ім
w= – І=– =
де a=
Як видно з (2.60), рівняння електромеханічної характеристики представляє собою гіперболу з асимптотами: вісь ординат, тобто І=0, та пряма w = –b (Рис. 2.56). Жорсткість характеристики зростає із збільшенням навантаження, а при незначних навантаженнях вона мала.
Рис. 2.56.
Характерно, що електромеханічна характеристика не перетинає вісь ординат. Із зменшенням струму стрімко збільшується швидкість до недопустимих меж, тому двигун із послідовним збудженням запускається в роботу з обов’язковим навантаженням. Момент двигуна на першій ділянці після підстановки (2.58) в (2.5) дорівнює M = cФ(І)І = сКзІ2, (2.61)
тобто він пропорційний квадрату струму якоря. Механічна характеристика двигуна отримується з електромеханічної (2.60) з урахуванням виразу для струму, знайденого з (2.61) І =
w= –. (2.62)
Механічна характеристика (2.62) також представляє собою гіперболу. 2) На другій ділянці магнітний потік дорівнює Фнас=const, тому електромеханічна та механічна характеристики, отримані з (2.57) та (2.61), мають вигляд як і для двигуна з незалежним збудженням, тобто представляють собою прямі.
w= – І (2.63)
Природна механічна та електромеханічна характеристики двигуна з послідовним збудженням відповідають увімкненню на номінальну напругу U=Uн при відсутності у колі додаткового електричного опору Rд. Отримані залежності механічних та електромеханічних характеристик дають загальні уявлення про електромеханічні властивості двигуна з послідовним збудженням. Для інженерних розрахунків вони не використовуються внаслідок значних похибок апроксимації кривої намагнічування.
2.1.2.1. Штучні механічні характеристики та способи керування швидкістю двигуна з послідовним збудженням
Згідно до рівняння механічної характеристики двигуна (2.62)
w= – =
де a=
є два способи керування швидкістю: 1) Зміна напруги живлення двигуна U; 2) Збільшення електричного опору кола RяS за рахунок увімкнення додаткового резистора Rд. 1) При зміні напруги живлення коефіцієнт b характеристики залишається постійним, тому асимптоти механічних характеристик залишаються незмінними. Момент короткого замикання при зменшенні напруги також зменшується
Мкз = сКзІ2кз = сКз(U/RяS)2 (2.65)
Відповідні штучні механічні характеристики представлені на рис. 2.57. Робочі точки на характеристиках, як відомо, визначаються перетином із характеристикою статичного моменту.
Рис. 2.57.
2) При увімкненні додаткового резистора Rд збільшується сумарний електричний опір кола двигуна RяS=Rя+Rоз+Rд і відповідно збільшується коефіцієнт характеристика b. При цьому момент короткого замикання (2.65) зменшується. Додатковий резистор Rд за умовами комутації змінюється ступенями шляхом закорочення відповідних секцій реостата контактами силових контакторів. Сімейство штучних механічних характеристик представлено на рис. 2.58.
Використовується також спосіб керування швидкістю за рахунок шунтування обмотки збудження додатковим резистором. Штучні механічні характеристики при цьому розташовуються вище природної.
Рис. 2.58.
2.1.2.2. Зміна напрямку руху (реверс) та пуск двигуна з послідовним збудженням
Для зміни напрямку руху двигуна є два способи: потрібно змінити напрямок струму в обмотці якоря чи обмотці збудження (Рис. 2.59). Одночасна зміна напрямків струмів за рахунок зміни полярності напруги живлення двигуна не призводить до реверсу. Механічні характеристики для прямого та зворотного напрямків руху симетричні відносно початку координат і представлені на рис. 2.60. Пуск двигуна з послідовним збудженням здійснюється аналогічно як і двигуна з незалежним збудженням, тобто за допомогою пускового реостата чи задатчика інтенсивності для керованих за напругою електроприводів (дивись пункт 2.1.1.4).
Рис. 2.59.
Рис. 2.60. 2.1.2.3. Режими гальмування двигуна з послідовним збудженням
Двигун із послідовним збудженням не підтримує режим рекуперативного гальмування, бо його механічна характеристика не перетинає вісь ординат. Двигун дозволяє реалізувати наступні режими гальмування: 1) Гальмування противмиканням; 2) Динамічне гальмування із самозбудженням; 3) Динамічне гальмування з незалежним збудженням. 1) Реалізація режиму гальмування противмиканням в статичному режимі можлива, якщо механізм створює активний статичний момент. Для цього в коло двигуна вводиться додатковий резистор Rд із таким опором, щоб робоча точка перейшла з І-го рушійного квадранта у ІV-й гальмівний (Рис. 2.61). При цьому змінюється напрямок швидкості двигуна, величина якої задається значенням Rд.
Рис. 2.61. До початку гальмування двигун працює в рушійному режимі в робочій точці 1 із швидкістю w1. При увімкненні додаткового резистора Rд двигун із робочої точки 1 перейде в точку 2 на новій механічній характеристиці, бо швидкість миттєво змінитися не може. На ділянці характеристики 2-3 двигун сповільнюється в рушійному режимі до зупинки, а на ділянці 3-4 розганяється в протилежному напрямку в режимі гальмування противмиканням. Точка 4 є новою робочою точкою двигуна, в якій він гальмує механізм, наприклад, лебідку при опусканні вантажу, забезпечуючи усталену швидкість w4. Збільшення цієї швидкості здійснюється збільшенням величини додаткового опору.
Режим гальмування противмиканням при реактивному статичному моменті реалізується тільки в перехідному процесі. Для гальмування механізму здійснюється реверс працюючого двигуна з обмеженням максимального гальмівного моменту за допомогою увімкнення в коло двигуна додаткового резистора Rд (Рис. 2.62). При перемиканні двигун переходить із статичної точки 1, в якій він працював, у точку 2 чи 3 на нових механічних характеристиках у залежності від величини додаткового опору Rд. На ділянках 2-4 чи 3-5 двигун сповільнюється в режимі гальмування противмиканням до зупинки. В точці зупинки 4 двигун з опором Rд1 буде продовжувати стояти під струмом, бо його момент менше статичного Мкз4<Мс. З точки 5 двигун з опором Rд2 почне розганятися у рушійному режимі у зворотному напрямку, бо момент короткого замикання Мкз5>Мс, прямуючи до нової статичної точки 6. В обох випадках при зупинці двигуна його потрібно відключити від живлення. Перевагою гальмування противмиканням є можливість керування моментом гальмування в значному проміжку, особливо при низьких швидкостях. Недоліком є низька енергетична ефективність, бо вся енергія від мережі та механізму втрачається у двигуні та резисторі, перетворюючись у тепло.
Рис. 2.62.
2) Динамічне гальмування із самозбудженням найчастіше застосовується в електроприводах транспортних та вантажопідйомних машинах, а також як аварійне, бо не потребує джерела живлення. Для реалізації гальмування працюючий двигун відключається від мережі й закорочується на додатковий резистор Rд. Поштовхом для виникнення гальмівного моменту є залишковий магнітний потік Ф0 у магнітопроводі двигуна при виконанні двох умов: · Напрямок струму в обмотці збудження у гальмівному режимі повинен співпадати за напрямком струму, який був до початку гальмування в рушійному режимі. Це необхідно для того, щоб новостворений струмом двигуна магнітний потік за напрямком співпадав із Ф0, інакше магнітопровід повністю розмагнітиться; · Сумарний електричний опір кола двигуна RяS=Rя+Rоз+Rд повинен бути менше критичного, величина якого визначається швидкістю двигуна
RяS < Rкр== ≈ = cKзw. (2.66)
Чим більший опір кола, тим при більшій швидкості починається збудження двигуна та відповідно режим гальмування. Механічні характеристики мають нелінійний характер, як показано на рис. 2.63. При невеликих навантаженнях гальмівний момент незначний, але він стрімко зростає після збудження двигуна, забезпечуючи прямолінійні характеристики при збільшенні моменту.
Рис. 2.63.
На рис. 2.63 представлено гальмування при реактивному статичному моменті Мс. Зі статичної точки 1 при швидкості w1 двигун із рушійного режиму переходить у режим гальмування в точку 2 чи 3 у залежності від значення додаткового опору Rд, створюючи гальмівний момент М2 чи М3. На ділянці характеристики 2-0 чи 3-0 двигун сповільнюється до зупинки. Якби статичний момент був активним, то після зупинки двигун почав би розганятися у зворотному напрямку в режимі гальмування до нової робочої точки, яка визначається перетином із механічною характеристикою механізму.
3) Для організації динамічного гальмування з незалежним збудженням тільки обмотка якоря відключається від джерела живлення і закорочується на додатковий резистор Rд. Обмотка збудження залишається підключеною до джерела живлення через струмообмежуючий резистор Rсо, за допомогою якого задається необхідний (номінальний) струм збудження. В цьому режимі гальмування двигун має механічні характеристики як і двигун з незалежним збудженням, тобто характеристики представляють собою прямі, які проходять через початок координат (Рис. 2.64). Величина гальмівного моменту М2 чи М3 задається величиною додаткового опору Rд. При реактивному статичному моменті Мс двигун зупиняється в початку координат, а при активному моменті розганяється до статичної швидкості у ІV-му квадранті. В режимі динамічного гальмування механічна енергія, яка поступає від механізму, перетворюється у двигуні та додатковому резисторі в тепло. Перевагою цього режиму є достатньо висока ефективність та простота реалізації, а недоліком – незначний гальмівний момент на низьких швидкостях.
Рис. 2.64.
2.1.2.4. Побудова природної та штучних характеристик двигуна з послідовним збудженням
Механічна та електромеханічна характеристика двигуна мають нелінійний вигляд. При невеликих навантаженнях, коли магнітне коло двигуна ненасичене, це гіперболи, які із збільшенням навантаження та насичення магнітного кола переходять у прямі. За паспортними даними природну характеристику побудувати неможливо. Для цього використовуються універсальні характеристики, які приводяться у довідниках для однієї серії двигунів, і представляють собою залежності у відносних одиницях швидкості та моменту двигуна від струму (Рис. 2.65). Побудова природних механічної та електромеханічної характеристики здійснюється у наступній послідовності: 1) На осі абсцис задається ряд струмів Іi*; 2) За універсальними характеристиками знаходяться відповідні швидкості wі * та моменти Мі*; 3) На основі паспортних даних обчислюються швидкості, моменти та струми в абсолютних одиницях Мі = Мі*·Мн , wі = wі*·wн , Іі = Іі*·Ін ; 4) За результатами попереднього пункту будується природна механічна та електромеханічна характеристика w = f(M) та w = f(I).
Рис. 2.65.
На основі природної характеристики за допомогою різних методів будуються штучні характеристики. Аналітичний метод ґрунтується на відношенні швидкостей на природній та штучній характеристиках. Для природної характеристики швидкість будь-якої точки дорівнює
wПі=,
де Rдв = Rя + Rоз – електричний опір двигуна, який приблизно можна знайти за паспортними даними
Відповідно для штучної характеристики
wШі=.
Тоді відношення швидкостей на характеристиках визначається виразом
wШі = wПі. (2.67)
За допомогою формули (2.67) будується штучна характеристика. При наявності додаткового опору Rд у колі двигуна в чисельник підставляється номінальна напруга Uн. Для розрахунку штучної характеристики при зміні напруги живлення U у чисельник підставляється Rд=0. Штучна характеристика будується в наступній послідовності: 1) За допомогою універсальної характеристики будується природна електромеханічна характеристика згідно до вищенаведеного; 2) Задається ряд струмів Іі, за якими на природній характеристиці знаходяться відповідні швидкості wПі; 3) За формулою (2.67), наприклад, при наявності додаткового опору в Rд, для відповідного струму Іі та wПі знаходяться швидкості для штучної характеристики wШі; 4) За результатами попереднього пункту наносяться точки швидкостей wШі на перетині з відповідними струмами Іі й отримується штучна електромеханічна характеристика w = f(I) (Рис. 2.66); 5) За допомогою універсальної характеристики М* = f(I*) знаходяться моменти Мi та будується штучна механічна характеристика w = f(M).
Рис. 2.66.
2.1.2.5. Динамічні властивості електромеханічного перетворювача двигуна з послідовним збудженням
Потужність кола якоря на порядок більша за потужність кола збудження, що обумовлює форсовану зміну потоку двигуна та необхідність врахування у динамічній моделі двигуна впливу вихрових струмів в полюсах та станині. Найчастіше цей вплив враховується за допомогою фіктивної короткозамкненої обмотки з числом витків Wвс та електричним опором Rвс, по якій протікає струм Івс. Після цього процес перетворення енергії у двигуні з послідовним збудженням описується наступною системою рівнянь
де Wз – число витків послідовної обмотки збудження.
Для практичного застосування рівнянь (2.68) з них виключається вихровий струм, шляхом ділення першого рівняння на
де
Коефіцієнт кола збудження kф при збільшенні струму до номінального Ін залишається практично незмінним, а потім починає стрімко зменшуватися при збільшенні насичення магнітного кола двигуна. В області перевантажень властивості двигуна з послідовним збудженням наближаються до властивостей двигуна з незалежним збудженням, бо магнітний потік стає практично сталим та рівним потоку насичення Фнас, проте при цьому не тільки повністю компенсується реакція якоря, а й збільшується результуючий магнітний потік на 10-20 %. Це обумовлює більшу в порівнянні з двигуном з незалежним збудженням перевантажувальну здатність двигуна. На основі рівнянь (2.69) будується відповідна структурна схема двигуна з послідовним збудженням (Рис. 2.67).
Рис. 2.67.
Наявність нелінійностей у вигляді перемноження змінних при створенні моменту та ЕРС двигуна, а також коефіцієнта кола збудження kф, що характеризує криву намагнічування, обумовлює складність аналітичного аналізу динамічних властивостей двигуна з послідовним збудженням.
2.1.3. Електромеханічні властивості двигуна постійного струму зі змішаним збудженням
Двигуни зі змішаним збудженням використовуються в ковальсько-штампувальних машинах, механізмах підйому та електротранспорту. Двигун має дві обмотки збудження: незалежну (НОЗ) та послідовну (ПОЗ), тому він має властивості двигуна з незалежним та послідовним збудженням, а також більші габарити та вищу вартість (Рис. 2.68). При проектуванні двигуна задається співвідношення потоків обмоток при номінальному струмі якоря на рівні Фпоз/Фноз=0,75¸1,0.
Рис. 2.68.
Двигуни зі змішаним збудженням випускаються з підмагнічуванням або розмагнічуванням основного магнітного потоку Фноз, який створюється незалежною обмоткою збудження
ФS = Фноз ± Фпоз. (2.70)
де “+” – підмагнічування, а “–“ – розмагнічування потоку.
Механічна та електромеханічна характеристика двигуна не мають аналітичного виразу, тому для їх побудови використовуються універсальні характеристики у відносних одиницях M* = f(I*), w* = f(I*), які подаються у довідниках для двигунів однієї серії. За їх допомогою та номінальними даними конкретного двигуна розраховуються природні та штучні характеристики згідно вищенаведеного пункту 2.1.2.4. Механічна характеристика двигуна зі змішаним збудженням на відміну від двигуна з послідовним збудженням перетинає вісь ординат, причому швидкість ідеального холостого ходу визначається магнітним потоком тільки незалежної обмотки збудження (Рис. 2.69).
Рис. 2.69.
Механічна характеристика двигуна з підмагнічуванням магнітного потоку має меншу жорсткість, ніж із розмагнічуванням. Для керування швидкості двигуна використовується зміна напруги якоря, зміна магнітного потоку незалежної обмотки збудження та введення додаткового електричного опору в коло якоря. Для гальмування застосовується рекуперативне гальмування, гальмування противмиканням та динамічне гальмування. При рекуперативному та динамічному гальмуванні послідовна обмотка збудження шунтується, тому в цих режимах двигун має прямолінійні механічні характеристики, як у двигуна з незалежним збудженням. В режимі ж гальмування противмиканням механічні характеристики мають нелінійний вигляд. Для зміни напрямку руху двигуна потрібно змінити напрямок струму тільки в обмотці якоря або одночасно в обох обмотках збудження.
Література: [1, с. 106-118], [2, с. 135-150].
СРС: Динамічні властивості двигуна зі змішаним збудженням. Схеми реверсу двигуна зі змішаним збудженням. Література: [16, с. 139-141], [1, с. 115-118].
Контрольні запитання: 1. Який вигляд має електромеханічна та механічна характеристика ДПС з послідовним збудженням. 2. Які є способи керування швидкістю ДПС з послідовним збудженням. 3. Які режими гальмування забезпечує ДПС з послідовним збудженням. 4. Як здійснити реверс ДПС з послідовним збудженням. 5. Що таке універсальні характеристики ДПС з послідовним та змішаним збудженням. 6. Як будується природна механічна характеристика ДПС з послідовним збудженням. 7. Переваги та недоліки ДПС з послідовним збудженням. ЛЕКЦІЯ 13
2.2. Електромеханічні властивості двигунів змінного струму
2.2.1. Електромеханічні властивості трифазного асинхронного двигуна
Асинхронний двигун (АД) є найпоширенішим двигуном серед усіх типів двигунів. Він має високу надійність, невелику масу, габарити та вартість. Недоліком двигуна є невеликий пусковий момент, споживання реактивної потужності, складні математичні залежності між його параметрами, тому якісна система керування реалізується за допомогою відносно складних алгоритмів. Переважна більшість АД використовується у нерегульованих електроприводах. Конструктивно двигун складається з нерухомого статора, в пазах якого знаходиться трифазна обмотка статора. Кінці обмотки для комутації виводяться до клемної коробки. Виводи початків обмоток фаз позначаються символами С1, С2, С3, а кінці - С4, С5, С6 . За допомогою підшипникових щитів усередині статора встановлюється рухомий ротор з обмоткою ротора. В залежності від виду обмотки ротора АД розділяються на найбільш поширені двигуни з короткозамкненим та на менш поширені з фазним ротором, умовне графічне позначення яких відповідно представлено на рис. 2.70а та рис. 2.70б. Короткозамкнена обмотка найчастіше виконується у вигляді білячої клітки. Три кінці обмотки фазного ротора за допомогою трьох мідних кілець та трьох електричних щіток виводяться до клемної коробки ротора.
а) б) Рис. 2.70.
Виводи трифазної обмотки статора можуть підключатися до мережі за схемою “зірка” (рис. 2.71а) або “трикутник” (рис. 2.71б).
а) б) Рис. 2.71.
Як видно з рис. 2.71, для схеми “зірка” лінійний струм дорівнює фазному Іл=Іф, а лінійна напруга становить Uл =Uф. Відповідно для схеми “трикутник” струм Іл=Іф, а напруга Uл =Uф, тому обмотку за схемою “зірка” можна вмикати на більшу в напругу, чим за “трикутником”, наприклад, на 380 та 220 В відповідно при забезпеченні незмінної потужності двигуна. Випускаються двигуни або тільки з однією схемою увімкнення “зірка” чи “трикутник”, чи двигуни, які дозволяють робити перемикання з однієї схеми на іншу. В останньому випадку комутація здійснюється в клемній коробці за допомогою перемичок між шпильками С1-С6 (Рис. 2.72).
Рис. 2.72.
При підключенні обмотки статора до мережі створюється магнітне поле, яке обертається із синхронною швидкістю
маючи синхронну частоту обертання
де f1 – частота напруги живлення обмотки статора, Гц; р – число пар полюсів двигуна.
Для стандартної мережі з частотою напруги f1=50 Гц існує відповідний ряд синхронних швидкостей у залежності від числа пар полюсів двигуна (Табл. 2.1). Тому при проектуванні ЕП та механізму потрібно заздалегідь спиратися на вказаний ряд швидкостей.
Таблиця 2.1.
Створене магнітне поле індукує ЕРС взаємоіндукції в обмотці статора Е1 та ротора Е2s
де W1, W2 – кількість витків обмоток статора та ротора; Kw1, Kw2 – коефіцієнти намотування обмоток статора та ротора; s – ковзання двигуна.
Під дією ЕРС Е2s в обмотці ротора протікає струм ротора І2, який, взаємодіючи з магнітним потоком Ф, створює момент двигуна М. Цей момент обумовлює обертання ротора із швидкістю w та визначає ковзання двигуна
В залежності від швидкості двигуна ковзання приймає значення відповідно до табл. 2.2. Таблиця 2.2.
Часто ковзання представляється у відсотках
Двигуни звичайного виконання мають номінальне ковзання в межах 1,5-6%. Для металургійних, кранових та інших механізмів випускаються двигуни з підвищеним ковзанням 8-12%. Так як ковзання однозначно зв’язане із швидкістю формулою (2.76), із якої
то механічна характеристика АД представляється також залежністю ковзання від моменту s=f(M). Згідно до (2.75) ЕРС ротора Е2s залежить від ковзання і при синхронній швидкості двигуна w=wc дорівнює нулю Е2s=0, що є ознакою роботи двигуна в точці ідеального холостого ходу. Частота ЕРС ротора Е2s та струму ротора І2 також залежить від ковзання
тобто із зменшенням ковзання частота в роторі зменшується і при наближенні швидкості двигуна до синхронної швидкості wc струм та ЕРС ротора наближаються за формою до постійного струму. Відношення ЕРС статора до ЕРС нерухомого ротора називається коефіцієнтом трансформації і використовується для приведення параметрів ротора до статора
де U1л н – номінальна лінійна напруга статора; Е2н – номінальна ЕРС ротора.
Г-подібна схема заміщення фази двигуна з теорії електричних машин (Рис. 2.73) використовується для знаходження виразу для моменту двигуна.
Рис. 2.73.
де U1 – фазна напруга обмотки статора; І1 – струм обмотки статора;
Іm – струм намагнічування, який створює магнітний потік Ф; Хm – індуктивний опір взаємоіндукції; R1, Х1– активний та індуктивний опори обмотки статора;
m1, m2 – кількість фаз обмоток статора та ротора.
Для трифазного двигуна з фазним ротором m1=m2=3, а для двигуна з короткозамкненим ротором m2=Z2, W2=0,5, Kw2=1. Згідно до рис. 2.73 струм ротора визначається залежністю
де Xk =X1 +X2’ – сумарний індуктивний опір.
Активна електромагнітна потужність трифазного АД, яка передається до ротора через повітряний зазор, з однієї сторони дорівнює
а з іншої
Після порівняння потужностей (2.81) та (2.82) отримується рівняння електромагнітного моменту асинхронного двигуна
Як видно з (2.83), момент двигуна залежить від квадрата напруги статора, тому АД дуже чутливий до зниження напруги живлення. Вираз для пускового моменту двигуна отримується з (2.83) при ковзанні s=1
Функція (2.83) має точки екстремуму за ковзанням, які знаходяться з рівняння
Це критичне ковзання
Критичному ковзанню відповідає критичний момент
В рівняннях (2.85) та (2.86) знак “– “ береться, якщо швидкість двигуна більша за синхронну w > wc. З урахуванням формул для критичного ковзання та моменту (2.85) та (2.86) рівняння моменту (2.83) перетворюється у формулу Клосса, яка використовується для аналітичної побудови м
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.238.22 (0.015 с.) |

 . (2.49)
. (2.49)
 , (2.52)
, (2.52) sin(Wt+y)= wсер– Dw sin(Wt+y), (2.56)
sin(Wt+y)= wсер– Dw sin(Wt+y), (2.56)


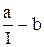 . (2.60)
. (2.60)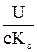 ; b=
; b=  .
.
 (2.64)
(2.64)
 ; b=
; b= 








 .
.
 , (2.68)
, (2.68) , а другого на – Rвс з наступним додаванням рівнянь
, а другого на – Rвс з наступним додаванням рівнянь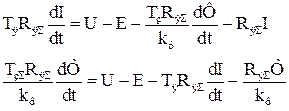 , (2.69)
, (2.69) – сумарна стала часу збудження.
– сумарна стала часу збудження.

 (2.71)
(2.71)



 , [рад/с] (2.72)
, [рад/с] (2.72) , [об/хв] (2.73)
, [об/хв] (2.73) (2.74)
(2.74) (2.75)
(2.75) – ЕРС нерухомого ротора;
– ЕРС нерухомого ротора; . (2.76)
. (2.76) .
. , (2.77)
, (2.77) , (2.78)
, (2.78) , (2.79)
, (2.79)
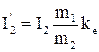 – приведений струм обмотки ротора;
– приведений струм обмотки ротора; – приведений активний опір обмотки ротора;
– приведений активний опір обмотки ротора; – приведений індуктивний обмотки ротора;
– приведений індуктивний обмотки ротора; , (2.80)
, (2.80) , (2.81)
, (2.81) . (2.82)
. (2.82) . (2.83)
. (2.83) . (2.84)
. (2.84) .
. . (2.85)
. (2.85)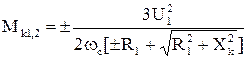 . (2.86)
. (2.86)


