
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод интегральных соотношенийСодержание книги
Поиск на нашем сайте
Метод интегральных соотношений (МИС) предложен Г.И. Баренблатом по аналогии с методами пограничного слоя. Основные предпосылки МИС: 1. Область течения, как в предыдущих методах, делится на возмущенную (длиной 2. В возмущенной области распределение давления представляется в виде многочлена по степеням координаты с коэффициентами, зависящеми от времени: · для прямолинейно-параллельного потока
· для плоскорадиального течения
Здесь число n членов многочлена выбирается в засисимости от желаемой точности решения. 3. Коэффициенты многочлена и закон перемещения границы возмущенной области определяют из внутренних граничных условий (на галереи или скважине), из условия неразрывности течения, условий гладкости кривой давления на границе зоны возмущения, а также из интегрального соотношения, определяющего сохранение материального баланса во всей возмушенной области. Для получения данного соотношения временную и пространственные части уравнения пьезопроводности следует умножить на простраственную переменную в степени n и поставить вместо давления выражение (4.53). После интегрирования полученного уравнения по размеру возмущенной области (от 0 до её границы) получим соотношения для определения коэффициентов ai(t). Из МИС можно получить, как частные случаи, метод ПССС (при n=1 – приток к галереи, n=0 – приток к скважине) и метод А.М. Первендяна (n=2) Пример решения методом интегральных соотношений задачи о нестационарном притоке упругой жидкости с дебитом Q к скважине радиуса rc из пласта с давлением pk. Согласно МИС, распределение давления в возмущенной области пласта
Коэффициенты ао, а1 и а2 находим из условий на забое скважины и на границе возмущенной области:
Определенные из этих условий коэффициенты имеют вид:
В результате получим следующее уравнение для давления
Закон движения границы возмущенной области
Значение средневзвешенного пластового давления
После интегрирования при пренебрежении членами содержащими
Т.о. распределение давления в возмущенной зоне имеет вид
Относительная погрешность уменьшается с течением времени и составляет -4,9%, если Т.о., МИС дает заниженные значения по сравнению с точным решением. Метод «усреднения» Метод «усреднения» предложен Ю.Д. Соколовым и Г.И. Гусейновым и заключается в том, что в уравнении пьезопроводности производная от давления по времени
значение которой определяется из начальных и граничных условий. В этом случае уравнение пьезопроводности
примет вид
Пример решения методом интегральных соотношений задачи о нестационарном притоке упругой жидкости с дебитом Q к скважине радиуса rc из пласта с давлением pk. При этом условия на забое скважины и на границе возмущенной области имеют вид:
Интегрируя уравнение (4.13) по r при учете граничных условий получим
Из условия гладкости кривой давления
Т.о. выражение для давления будет
Уравнение для определения закона движения возмущенной области находим также из уравнения материального баланса
Относительная погрешность метода при определении депрессии не превышает 5%.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Определяющие формы пластовой энергии при упругом режиме. 2. Определяющие формы пластовой энергии при упруго-водонапорном режиме. 3. Какие условия определяют замкнуто-упругий режим? 4. Условия, определяющие жестководонапорный режим. 5. Зависимость скорости протекания неустановившихся процессов от проницаемости, вязкости и коэффициентов объёмной упругости жидкости и пласта. 6. Коэффициент объёмной упругости жидкости. 7. Упругий запас. 8. Чему равен коэффициент упругоёмкости пласта? 9. Коэффициентом пьезопроводности для упругой жидкости. 10. Коэффициентом пьезопроводности для газовых пластов.
11. Параметр Фурье. 12. Уравнение пьезопроводности упругой жидкости и его вывод. 13. Правило Лопиталя. 14. Интегрально-показательная функция и ее свойства. 15. Уравнение КВД. Области использования. 16. Пьезометрические кривые при пуске скважины в конечном пласте с открытой внешней границей с постоянным дебитом. 17. Пьезометрические кривые при пуске скважины в конечном пласте с открытой внешней границей с постоянным забойным давлением. 18. Изменение дебита скважины с течением времени при постоянном забойном давлении. 19. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном дебите. 20. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении. 21. Изменение дебита скважины с течением времени при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении. 22. Уравнение КВД для периодически работающей скважины. 23. Как зависит угол наклона КВД от проницаемости.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.240 (0.008 с.) |

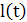 или радиуса
или радиуса  ) и невозмущенную.
) и невозмущенную. (4.53)
(4.53)
 (4.54)
(4.54) возьмём в виде многочлена первой степени
возьмём в виде многочлена первой степени
 при
при  (забое скважины);
(забое скважины); при
при  ;
; при
при  (условие гладкости кривой давления
(условие гладкости кривой давления 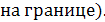
 при выводе слагаемыми, пропорциональными
при выводе слагаемыми, пропорциональными 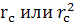 , пренебрегли.
, пренебрегли. (4.55)
(4.55) находится из уравнения материального баланса
находится из уравнения материального баланса (4.36)
(4.36) в возмущенной области
в возмущенной области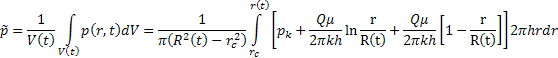
 имеем
имеем 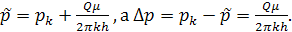 Объём возмущенной зоны V
Объём возмущенной зоны V  Подставив данные соотношения в (4.36), после преобразований получим
Подставив данные соотношения в (4.36), после преобразований получим  Отсюда после интегрирования получим
Отсюда после интегрирования получим
 (4.37)
(4.37) при
при 
 -4%, если fo = 103; -3.2%, если fo = 104.
-4%, если fo = 103; -3.2%, если fo = 104.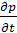 усредняется по всей возмущенной области и заменяется некоторой функцией времени
усредняется по всей возмущенной области и заменяется некоторой функцией времени dr. (4.38)
dr. (4.38) . (4.12)
. (4.12) (4.13)
(4.13)
 находим функцию
находим функцию .
. (4.14)
(4.14)



