
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения потенциального движения для пористой средыСодержание книги
Поиск на нашем сайте
Потенциальным течением будем называть течение, при котором проекции массовой скорости на оси ортогональной системы координат будут являться производными некоторой функции по направлениям данных осей. Фильтрационное течение в горных породах подчиняется закону Дарси и, следовательно, потенциально. Потенциалом поля скоростей в данном случае является функция
Равенство (2.28) можно переписать в виде
или, учитывая закон Дарси,
Здесь r`u – вектор массовой скорости фильтрации; gradj – градиент j, направленный в сторону быстрейшего возрастания j. Уравнение (2.30) – это закон Дарси, записанный для потенциального течения. Подставляя (2.30) в (2.4), получаем
а для установившегося течения
Уравнения (2.31) и (2.32) являются основными уравнениями потенциального фильтрационного течения и называются уравнениями Лапласа относительно функции j, а оператор Dj оператором Лапласа. В скалярной форме оператор Лапласа имеет вид
где (a) – декартовые координаты; (b) – сферические координаты; (c) – цилиндрические координаты.
Уравнение Лапласа имеет два практически важных свойства: · сумма частных решений является решением уравнения Лапласа; · произведение частного решения на константу – также решение.
Данные свойства приводят к принципу суперпозиции – сложения фильтрационных течений. Начальные и граничные условия
Выше было показано, что уравнения фильтрации сводятся к одному уравнению второго порядка относительно потенциала. В связи с этим, рассмотрим начальные и граничные условия для данного уравнения.
Начальные условия j = jо (x,y,z) при t = 0, если при t = 0 пласт не возмущён, тоj = jо = const. Граничные условия
Число граничных условий равно порядку дифференциального уравнения по координатам. Граничные условия задаются на границах пласта (внешние) и на забое скважины (внутренние). А) Внешняя граница Г 1)постоянный потенциал j (Г,t)= j к=const, т.е. граница является контуром питания; 2) постоянный переток массы через границу G = F r `u = const, т.е. используя уравнение (2.30),
3) переменный поток массы через границу 4) замкнутая внешняя граница 5) бесконечный пласт limx®¥ j(Г,t) = jк = const. у®¥ В) Внутренняя граница
1) постоянный потенциал на забое скважины, радиуса rc j (rc, t)= j c=const; 2) постоянный массовый дебит (при условии выполнения закона Дарси) 3) переменный потенциал на забое j (rc,t)=f2(t) при r=rc; 4) переменный массовый дебит
5) неработающая скважина
Замыкающие соотношения
Для полного замыкания системы уравнений фильтрационного течения необходимо знание зависимостей r, m, k, μ от давления.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.107 (0.01 с.) |

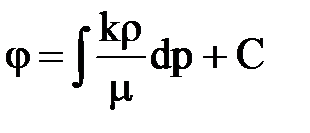 . (2.28)
. (2.28) (2.29)
(2.29)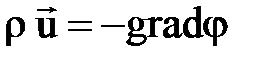 . (2.30)
. (2.30)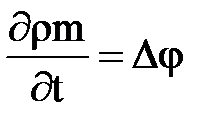 , (2.31)
, (2.31)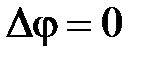 . (2.32)
. (2.32)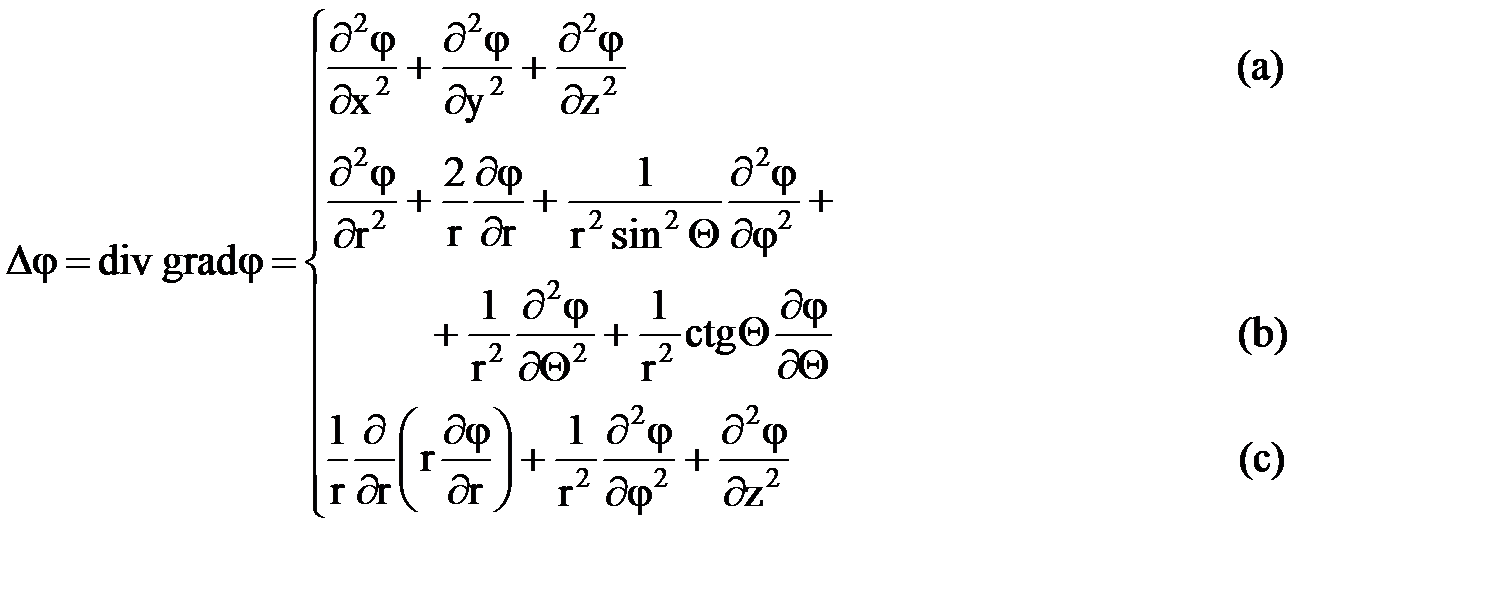 ,
,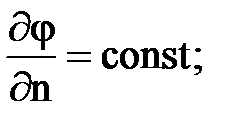
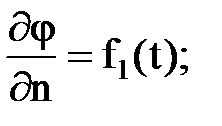
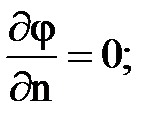
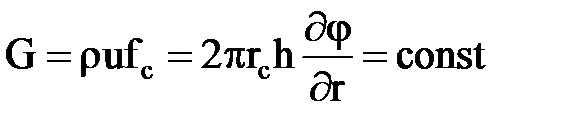 или
или 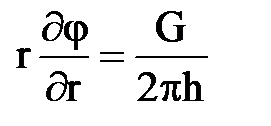 при r=rc;
при r=rc;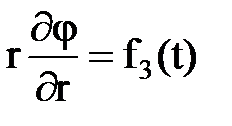 при r=rc;
при r=rc;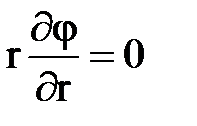 при r=rc.
при r=rc.


