
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплекс-метод решения задач линейного программированияСодержание книги
Поиск на нашем сайте
Симплексный метод в настоящее время получил широчайшее практическое применение и стал универсальным методом линейного программирования. Рассмотрим следующую задачу линейного программирования, заданную в каноническом виде:
При решении задачи линейного программирования симплекс-методом требуется, чтобы система уравнений (2) была приведена к допустимому виду, какие-то из переменных — базисные должны быть выражены через остальные переменные, которые называются свободными, причем в выражениях для базисных переменных свободные члены должны быть неотрицательными. Например, система
где В этой системе переменные Переменные Пусть целевая функция
Каждому шагу процесса решения задачи симплекс-методом соответствует своя таблица, таким образом, решение задачи линейного программирования можно представить в виде некоторой последовательности таблиц. Напомним, что рассматривается задача следующего вида:
при условиях:
Или в допустимом виде:
при условиях:
Составим первую симплекс-таблицу. Таблица 4
1. Выясним, имеются ли отрицательные коэффициенты в выражении (1) при переменных 2. Пусть в последней строке имеется положительное число, например, - 3. Пусть в столбце, отмеченном стрелкой, имеются положительные числа, то имеем третьей случай, и надо сделать шаг. Пусть, например, Элемент таблицы, стоящий на пересечении отмеченных столбца и строки, называется разрешающим. 4. Перестраиваем таблицу. Для этого умножаем выделенную строку на такое число, что бы на месте разрешающего элемента появилась 1, то есть на 5. К новой таблице применяется тот же метод. Ее анализируют на первый случай, второй случай и третий случай. В третьем случае строится еще одна таблица. Процесс продолжается до тех пор, пока не придем к первому или второму случаю.
Пример 1. Определить минимальное значение функции
Решение Запишем задачу в каноническом виде:
при условиях:
Расширенная матрица
Таким образом, Приведем систему к допустимому виду, выразив базисные переменные через свободные:
Целевая функция изначально оказалась записанной только через свободные переменные: Система уравнений
записана в том виде, в каком будем ее использовать при составлении таблицы. Из выражения для целевой функции получим следующее равенство Заполним таблицу 1. Таблица 1
В последней строке есть положительный коэффициент – это коэффициент в столбце Заполним таблицу 2. В базисных переменных Таблица 2
Умножаем вторую строку таблицы 2 и складываем с соответствующими значениями первой строки таблицы 1. Результат записываем в первую строку таблице 2. В столбце при переменной Умножаем вторую строку таблицы 2 на -1 и складываем с соответствующими значениями четвертой строки таблицы 1 и результат записываем в четвертой строке таблицы 2. В столбце при переменной В последней строке есть положительное число – коэффициент в столбце при переменной Заполняем таблицу 3. Умножаем выделенную строку на Таблица 3
Третью строку таблицы умножаем на 3 и складываем с первой строкой, умножаем на 2 и складываем со второй строкой, умножаем на -1 и складываем с четвертой строкой таблицы 2. В таблице 3 последняя строка не имеет положительных чисел в последних пяти столбцах. Значит, достигнуто оптимальное решение. Базисные переменные Минимальным значением целевой функции является свободный член в последней строке Пример 2. Найти максимальное значение функции: Метод искусственного базиса
при условиях:
Решение. Сведем задачу на максимум к задаче на минимум. Для этого целевую функцию умножим на (-1):
Для решения задачи симплекс-методом приведем систему уравнений к допустимому виду. Запишем расширенную матрицу системы уравнений и приведем ее к трапециевидному виду:
Следовательно, система уравнений совместна и неопределенная. По матрице трапециевидного вида восстановим систему:
Переменные
Получим систему уравнений допустимого вида. Выразим целевую функцию
Таким образом, задачу можно сформулировать следующим образом:
Для составления первой симплекс - таблицы запишем задачу в виде:
при условиях:
Заполним первую симплекс-таблицу. Таблица 1
В последней строке есть положительный коэффициент в столбце переменной Строим вторую таблицу. Для этого умножаем выделенную стрелкой строку на дробь Умножаем вторую строку новой таблицы на 1 и складываем с первой, умножаем на 1 и складываем с третьей, умножаем на -5 и складываем с четвертой строкой старой таблицы.
Таблица 2
В новой таблице последняя строка не имеет положительных чисел в последних пяти столбцах. Значит, достигнуто оптимальное решение. Базисным решением для переменных
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

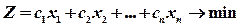 , (1)
, (1)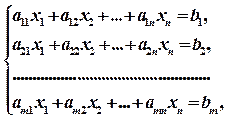 (2)
(2)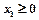 ,
, 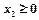 , …,
, …, 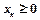 .
.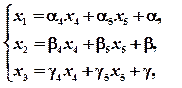 (3)
(3)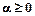 ,
, 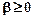 ,
, 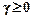 является системой допустимого вида.
является системой допустимого вида.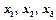 — базисные. Набор этих переменных (неизвестных) называется допустимым базисом переменных.
— базисные. Набор этих переменных (неизвестных) называется допустимым базисом переменных.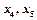 — свободные.
— свободные.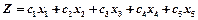 (4), а система уравнений приведена к допустимому виду (3). Заменив в выражении (4) каждую базисную переменную ее выражением через свободные переменные, целевую функцию можно записать в виде:
(4), а система уравнений приведена к допустимому виду (3). Заменив в выражении (4) каждую базисную переменную ее выражением через свободные переменные, целевую функцию можно записать в виде: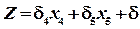 (5)
(5)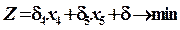 , (1)
, (1)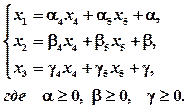 (2)
(2)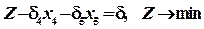 , (3)
, (3)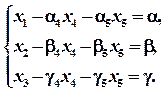 (4)
(4)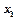
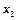
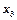
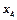
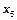
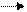
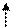 -δ4
-δ4
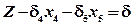 , то есть являются ли эти коэффициенты положительными в таблице. Если положительных коэффициентов в таблице 4 нет, то имеем первый случай, и базисное решение, отвечающее данному базису, является оптимальным.
, то есть являются ли эти коэффициенты положительными в таблице. Если положительных коэффициентов в таблице 4 нет, то имеем первый случай, и базисное решение, отвечающее данному базису, является оптимальным.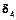 . Отметим столбец, в котором оно находится, вертикальной стрелкой. Если все числа в этом столбце отрицательные, то имеем второй случай, и задача решения не имеет.
. Отметим столбец, в котором оно находится, вертикальной стрелкой. Если все числа в этом столбце отрицательные, то имеем второй случай, и задача решения не имеет.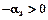 и
и 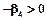 , находим
, находим 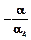 и
и 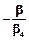 , а затем выбираем из них наименьшее. Пусть это будет
, а затем выбираем из них наименьшее. Пусть это будет 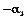 , горизонтальной стрелкой.
, горизонтальной стрелкой.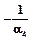 . Полученные результаты записываем в новой таблице в той же строке. Затем к каждой из оставшихся строк таблицы 4, включая последнюю строку, прибавляем вновь полученную строку, умноженную на такие числа, чтобы в клетках отмеченного столбца появились нули. Полученные результаты записывают в новую таблицу.
. Полученные результаты записываем в новой таблице в той же строке. Затем к каждой из оставшихся строк таблицы 4, включая последнюю строку, прибавляем вновь полученную строку, умноженную на такие числа, чтобы в клетках отмеченного столбца появились нули. Полученные результаты записывают в новую таблицу.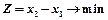 при условиях
при условиях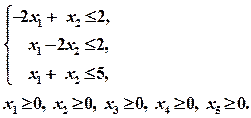
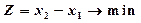
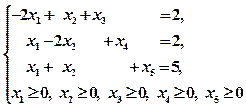
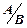 системы:
системы: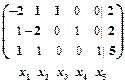 ~
~ 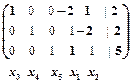 ,
,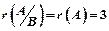 , и в системе три базисных переменных -
, и в системе три базисных переменных - 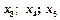 и две свободных -
и две свободных - 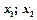 .
.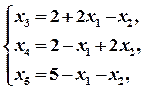 (5)
(5)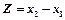 (поэтому выражения (5) нам не пригодились).
(поэтому выражения (5) нам не пригодились).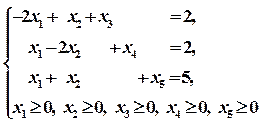
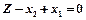 (эти коэффициенты при переменных вносятся в нижнюю строку таблицы).
(эти коэффициенты при переменных вносятся в нижнюю строку таблицы).

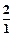
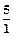
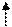
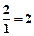 и
и 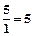 . Так как 2 < 5, то выделяем горизонтальной стрелкой строку при базисной переменной
. Так как 2 < 5, то выделяем горизонтальной стрелкой строку при базисной переменной 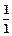 и записываем результат вместо этой строки.
и записываем результат вместо этой строки. 3
3
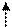 1
1
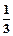 и записываем результат вместо этой строки.
и записываем результат вместо этой строки.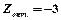
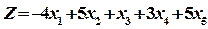
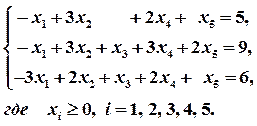
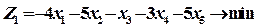 .
.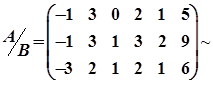


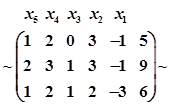
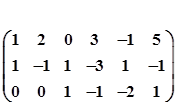
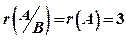 .
.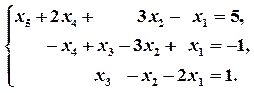
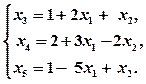
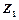 через свободные переменные:
через свободные переменные: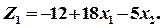
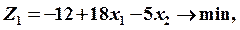
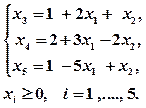
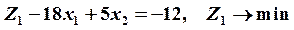
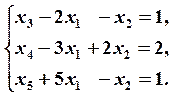
 -1
-1
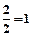
 5
5
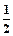 и записываем результат вместо этой строки в новую таблицу (таблица 2).
и записываем результат вместо этой строки в новую таблицу (таблица 2).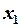 =0,
=0, 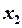 =1,
=1, 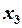 =2,
=2, 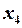 =0,
=0, 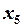 =2,
=2,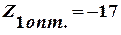 ,
, 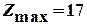 .
.


