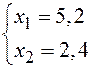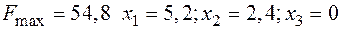Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимно двойственные задачи линейного программированияСодержание книги
Поиск на нашем сайте
Алгоритм построения взаимно-двойственных задач
Рассмотрим пару задач линейного программирования, связанных между собой симметричными зависимостями:
Такие задачи называют парой двойственных задач линейного программирования (или просто двойственной парой).
Пример 1. Построить задачу, двойственную следующей задаче линейного программирования:
Решение Умножим первое ограничение – неравенство на -1. Задача примет вид задачи (2) симметричной пары двойственных задач:
Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функцию.
Функция Умножаем коэффициенты при
Данная сумма меньше или равна коэффициенту при
Неравенство имеет вид «
Все переменные двойственной задачи удовлетворяют неотрицательности, потому что все ограничения исходной задачи – неравенства. Поскольку все ограничения задачи (1) имеют вид Окончательно двойственная задача имеет вид:
Пример 2. Построить задачу, двойственную данной задаче линейного программирования:
Решение Будем использовать условия, которым должны удовлетворять двойственные задачи. Умножим ограничения – неравенства на (-1), так как в задаче на максимум они должны иметь вид «
Составим двойственную задачу:
Переменная В теории двойственности есть теоремы, которые позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие.
Теорема 1. Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение, причем значения целевых функций задач на своих оптимальных решениях совпадают. Если же одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений. Теорема 2. Для того, чтобы допустимые решения
Иначе, если при подстановке оптимального решения в систему ограничений i-е ограничение исходной задачи выполняется как строгое неравенство, то i-я координата оптимального решения двойственнойзадачи равна нулю, и, наоборот, если i-я координата оптимального решения двойственной задачи отлична от нуля, то i-е ограничение исходной задачи удовлетворяется оптимальным решением как равенство.
Пример 3. Найти решение исходной задачи, зная решения двойственной и используя вторую теорему двойственности.
Решение Составим двойственную задачу:
Оптимальное решение двойственной задачи:
Подставим оптимальное решение
По теореме 2 следует, что соответствующие координаты оптимального решения исходной задачи (двойственной задачи), равны нулю Учитывая это, из системы ограничений исходной задачи получим:
Оптимальное решение исходной задачи:
Ответ:
Пример 4. Для ЗЛП построить двойственную задачу. Найти решение исходной задачи, зная решения двойственной:
Решение. Двойственная задача:
Поскольку второе условие исходной задачи записано в виде равенства, то переменная Решим двойственную задачу средствами Ms.Excel:
Поскольку
Ответ в исходной задаче:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.008 с.) |

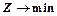 , а в задаче (2) - максимизировать:
, а в задаче (2) - максимизировать: 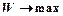 ;
;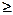 , все ограничения задачи (2) – неравенства –вида
, все ограничения задачи (2) – неравенства –вида 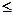 ;
;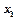 ,
, 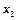 ,…,
,…, 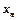 задач (1) и при переменных
задач (1) и при переменных 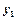 ,
, 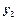 , …,
, …, 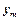 задачи (2) являются взаимно транспонированными;
задачи (2) являются взаимно транспонированными;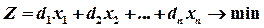
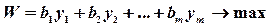
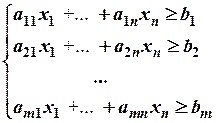
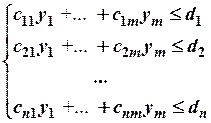
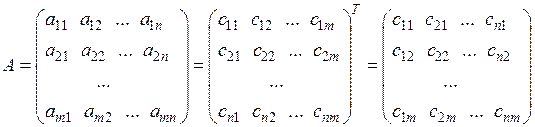
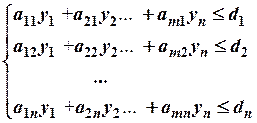
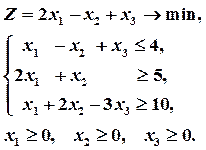
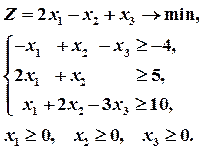
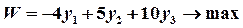 .
.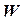 максимизируется, так как целевая функция исходной задачи минимизируется.
максимизируется, так как целевая функция исходной задачи минимизируется.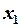 на соответствующие переменные двойственной задачи и складываем их:
на соответствующие переменные двойственной задачи и складываем их: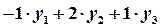 .
.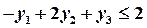 .
.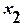 ,
, 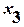 ):
):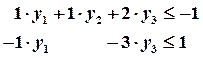
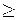 , то переменные задачи (2)все неотрицательны:
, то переменные задачи (2)все неотрицательны: 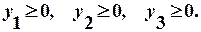
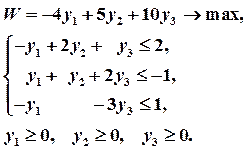
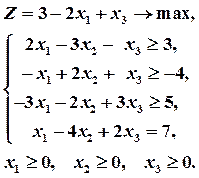
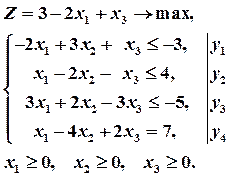
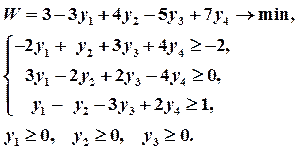
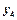 , соответствующая ограничению равенства, может быть любого знака.
, соответствующая ограничению равенства, может быть любого знака.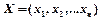 ,
, 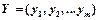 являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:
являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства: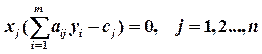 (1)
(1)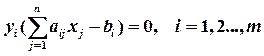 (2)
(2)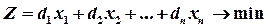
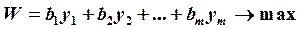
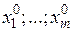 в систему ограничений
в систему ограничений
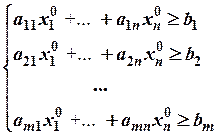 Пусть, например,
Пусть, например, 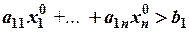 , тогда
, тогда 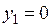 Если, например,
Если, например, 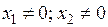 , то
, то
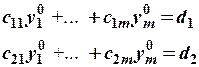
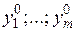 в систему ограничений
в систему ограничений
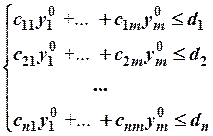 Пусть, например,
Пусть, например, 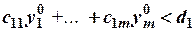 , тогда
, тогда  Если, например,
Если, например,  , то
, то
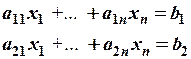
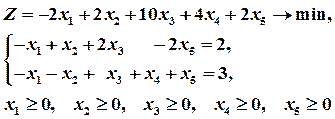
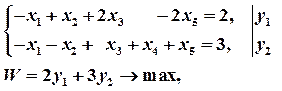
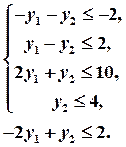
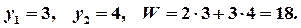
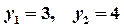 в систему ограничений. Получим, что, первое, второе и пятое ограничения выполняются как строгие неравенства.
в систему ограничений. Получим, что, первое, второе и пятое ограничения выполняются как строгие неравенства.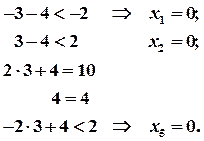
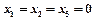 .
.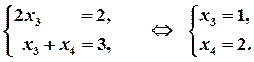
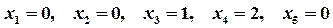 .
.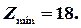

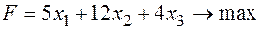
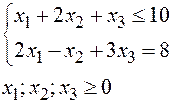
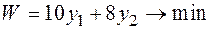
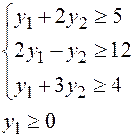
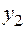 может быть любого знака.
может быть любого знака.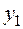 и
и 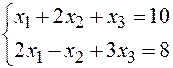 , а как видно из таблицы Excel, третье ограничение оптимальными значениями удовлетворяется в виде строгого неравенства, значит,
, а как видно из таблицы Excel, третье ограничение оптимальными значениями удовлетворяется в виде строгого неравенства, значит, 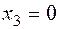 , т.е.
, т.е.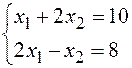 , решая систему, получаем:
, решая систему, получаем: