
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел II. Молекулярная физика, термодинамика.
Основные формулы. 1.Количество вещества однородного газа (в молях) Где N - число молекул газа; NА - число Авогадро (NА =6.02×1023 моль-1); т - масса газа; m - молярная масса газа. Если система представляет смесь нескольких газов, то количество вещества системы: v=v1+v2+……+vn= где vi, Ni, mi, mi - соответственно количество вещества, число молекул, масса, молярная масса i- й компоненты. 2.Уравнение Менделеева- Клайперона (уравнение состояния идеального газа):
где т - масса газа; m - молярная масса газа; R - универсальная газовая постоянная (R =8.31 Дж/(моль×К)); v=m/m - количество вещества; Т - термодинамическая температура Кельвина. 3.Опытные газовые законы, являющиеся частными случаями уравнения Менделеева- Клайперона для изопроцессов: а) закон Бойля- Мариотта (изотермический процесс- Т = const): p×V= const, или для двух состояний: p1×V1=p2×V2, где p1 и V1 – давление и объем газа в начальном состоянии, а p2 и V2 – давление и объем газа в конечном состоянии. б)закон Гей- Люссака (изобарический процесс- р =const): V/Т= const, или для двух состояний: V1/Т1= V2/Т2, где Т1 и V1 – температура и объем газа в начальном состоянии, а Т2 и V2 – температура и объем газа в конечном состоянии. в)закон Шарля (изохорический процесс- V =const): р/Т= const, или для двух состояний: р1/Т1= р2/Т2, где Т1 и р1 – температура и давление газа в начальном состоянии, а Т2 и р2 – температура и давление газа в конечном состоянии. г)объединенный газовый закон: рV/Т= const, или для двух состояний: р1×V1/Т1=р2× V2/Т2, где Т1, р1 и V1 – температура, давление и объем газа в начальном состоянии, а Т2, р2 и V2 – температура, давление и объем газа в конечном состоянии. 4.Закон Дальтона, определяющий давление смеси газов: p=р1+р2+…pn, где рi- парциальные давления компонентов смеси, n- число компонентов смеси. 5.Молярная масса смеси газов: 6.Массовая доля wi i- го компонента смеси газа (в долях единицы или процентах): wi=тi/т, где т - масса смеси. 7.Концентрация молекул (число молекул в единице объема):
где: N - число молекул, содержащихся в данной системе; r - плотность вещества. 8.Основное уравнение молекулярно- кинетической теории газов:
где < wП> -средняя кинетическая энергия поступательного движения молекулы.
9.Средняя кинетическая энергия поступательного движения молекулы: < wП> = где k =1.38×10-23 Дж/К постоянная Больцмана. 10.Средняя полная кинетическая энергия молекулы: < wП> = 11.Зависимость давления газа от концентрации молекул и температуры: p=n×k×T. 12.Скорости молекул: средняя квадратичная: < Vкв >= средняя арифметическая: < V >= наиболее вероятная: VВ= 13.Относительная скорость молекулы: u=V/VB, где V – скорость данной молекулы. 14. Средняя длина свободного пробега молекул: <l>= 15. Кинетические коэффициенты - коэффициенты диффузии, теплопроводности и внутреннего трения: D= c= h= 16.Удельные теплоемкости газа при постоянном объеме (СV) и при постоянном давлении (СР): СV= 17.Связь между удельной (с) и молярной (С) теплоемкостями: с=С/m; С=с× m. 18.Уравнение Роберта Майера: СР - СV = R. 19.Внутренняя энергия идеального газа: 20.Первое начало термодинамики: Q= D U+A, где Q - теплота, сообщенная системе; D U - изменение внутренней энергии системы; А - работа, совершенная системой против внешних сил. 21.Работа расширения газа: в общем случае: при изобарическом процессе: A=p(V2-V1); при изотермическом процессе: при адиабатическом процессе: где g=СР/СV- показатель адиабаты. 22.Уравнение Пуассона, связывающее параметры идеального газа при адиабатическом процессе: pVg= const; 23.Термический к.п.д. цикла: 24.Термический к.п.д. цикла Карно:
ПРИМЕР ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ. Задача 1. Тело вращается вокруг неподвижной оси по закону х = А + В × t + С × t 2, где А =10 рад; В = 20 рад/с; С =2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0.1 м от оси вращения для момента времени t = 4 с.
Так как векторы ` аt и` аn взаимно перпендикулярны, то абсолютное значение ускорения: Тангенциальное и нормальное ускорение точки, вращающегося тела выражаются формулами: ae = e×r и an = w2×r, где w - угловая скорость тела; e - его угловое ускорение. Подставляем выражения для аt и аn в формулу, получим
Угловую скорость w найдем взяв производную от угла поворота по времени: w = w =[20+2(-2)×4] = 4 рад/с. Угловое ускорение найдем, взяв первую производную от угловой скорости по времени: e = Это выражение не содержит времени; следовательно, угловое ускорение заданного движения постоянно. Подставляя найденные значения w, e и заданное значение r в полученную формулу, получим:
Решение: Тележку и ящик можно рассматривать как систему двух неупругих взаимодействующих тел. Но эта система не замкнута, так как сумма внешних сил, действующая на систему: двух сил тяжести m1`g и m2`g и силы реакции `N2 не равна нулю. Поэтому применять закон сохранения импульса к системе ящик- тележка нельзя.
Но так как проекция суммы указанных сил на направление оси х, совпадающей с направлением рельсов, равна нулю, то составляющую импульса системы в этом направлении можно считать постоянной, т.е. р1х + р2х = Выразив в этом равенстве импульсы тел через их массы и скорости, учитывая, что р2х =0 (тележка до взаимодействия покоилась), а также что после взаимодействия оба тела системы движутся с одной и той же скоростью u: m1×v1x =(m1 + m2) u, или m1×v1×cosa =(m1 + m2) u, где v1 - скорость ящика перед падением на тележку; v1x = v1×cosa- проекция этой скорости на ось x. Отсюда выразим искомую скорость: Скорость v1 определим из закона сохранения энергии: Подставив найденное значение v1 в формулу для нахождения u получим:
Подставив сюда числовые значения величин и произведя вычисления получим:
Задача 3. На спокойной воде пруда перпендикулярно берегу и носом к нему стоит лодка массой М и длиной L. На корме стоит человек массой m. На какое расстояние s удалится лодка от берега, если человек перейдет с кормы на нос лодки? Силами трения и сопротивления пренебречь. Решение: Согласно следствию из закона сохранения импульса внутренние силы системы тел не могут изменить положение центра масс системы. Применяя это следствие к системе человек- лодка, можно считать, что при перемещении человека по лодке центр тяжести системы не изменит своего положения, т.е. останется на прежнем расстоянии от берега. Пусть центр тяжести системы человек- лодка находится на вертикали, проходящей в начальный момент времени через точку С1 лодки (рис.3), а после перемещения лодки – через другую точку С2. Так как эта вертикаль неподвижна относительно берега, то искомое перемещение s лодки относительно берега равно перемещению лодки относительно вертикали. А это последнее легко определить по перемещению центра тяжести О лодки. Как видно из рис 3, в начальный момент времени точка О находится на расстоянии а1 слева от вертикали, а после перехода человека- на расстояние а2 справа от неё.
Для определения a1 и a2 воспользуемся тем, что относительно центра тяжести системы моменты сил тяжести лодки и человека должны быть равны. Для точки С1 получим: М × g×a1 = m×g× (l - a1) Откуда после сокращения на g получим: Для точки С2 имеем: М × g×a2 = m×g× (L - l - a2), откуда Подставив выражения a1 и a2 в формулу получим:
Задача 4. Шар массой m1, движущийся горизонтально со скоростью v1 столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму? Решение: Доля e кинетической энергии, переданной первым шаром второму выразится соотношением: Как видно из этой формулы, для определения e надо найти u2. При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: закона сохранения импульса и закона сохранения механической энергии. Пользуясь этими законами найдем u2. По закону сохранения импульса, учитывая, что второй шар до удара покоился, получим: m1×v1 = m1×u1+ m2×u2 . По закону сохранения механической энергии: Решая совместно эти уравнения найдем: Подставив это выражения для u2 в формулу и сократив на v1 и m1, получим: Из полученного выражения видно, что доля передаваемой энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами. Задача 5. Через блок в виде сплошного диска, имеющего массу m =80 г (рис 4), перекинута тонкая, гибкая нить, к концам которой подвешены грузы с массами m1 =100 г и m2 =200 г.с каим ускорением будут двигаться грузы, если их предоставить самим себе. Трением и массой нити пренебречь. Решение: Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдель
m1×g- T1=-m1×a. Уравнение для второго груза запишется аналогично: m2×g- T2=m2×a. Под действием двух моментов сил Т’1 × r и Т’2 × r относительно оси, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение e (e = а/r). Согласно основному уравнению динамики вращательного движения: Т’2 × r - Т’1 × r = Jz×e,где Сила Т’1 согласно третьему закону Ньютона по абсолютному значению равна силе Т1. Соответственно и сила Т’2 равна силе Т2. Воспользовавшись этим, подставим в уравнение вместо Т’1 и Т’2 выражения для Т1 и Т2, получив их предварительно из уравнений по второму закону Ньютона: (m2×g- m2×a) r - (m1×g + m1×a) r = после сокращения на r и перегруппировки членов найдем интересующее нас ускорение: Отношение масс в правой части формулы есть величина безразмерная, поэтому массы можно выразить в граммах, как они даны в условии задачи. Ускорение g надо выразить в единицах СИ. После подстановки получим:
Задача 6. Маховик в виде сплошного диска радиусом R =0.2 м и массой m =50 кг раскручен до частоты вращения n1 = 4800 мин-1 и предоставлен самому себе. Под действием сил трения маховик остановился через t =50 с. Найти момент М сил трения. Решение: Для решения задачи воспользуемся основным уравнением динамики вращательного движения в виде: dLz=Mz×dt, где dLz – изменение момента импульса маховика, вращающегося относительно оси z, совпадающей с геометрической осью маховика за интервал dt; Мz - момент внешних сил (в нашем случае момент сил трения), действующих на маховик относительно той же оси. Момент сил трения можно считать не изменяющимся с течением времени (Mz = const), поэтому интегрирование полученного уравнения приводит к выражению D L = Mz× D t. При вращении твердого тела относительно неподвижной оси изменение момента импульса D L = Jz× D w, где Jz – момент инерции маховика относительно оси z; D w - изменение угловой скорости маховика. Приравняв правые части равенства получим: Mz× D t = Jz× D w, откуда Момент инерции маховика в виде сплошного цилиндра определяется по формуле: Изменение угловой скорости D w = w2-w1 выразим через конечную n2 и начальную n1 частоты вращения, пользуясь соотношением w=2×p×n: D w=w2-w1=2×p×n2 -2×p×n1=2×p× (n2-n1). Подставив в формулу найденные выражения Jz и D w, получим:
Выпишем величины, входящие в эту формулу в СИ и произведем вычисления: m = 50 кг; R =0.2 м; n2 =480 мин-1=480/60 с-1=8 с-1; n2= 0; D t = 50 с.
Знак «минус» показывает, что силы трения оказывают на маховик тормозящее действие. Задача 7. Определить плотность смеси газа, состоящего из 6 г водорода и 42 г азота, находящихся при нормальных условиях.
Решение. Используем определение плотности: Объем, занимаемый смесью, определим, используя уравнение состояния идеального газа: pV=vRT, где v – число молей газа. Для смеси v=v1+v2= Тогда получаем V=( Проверим размерность: Вычислим значение плотности: Ответ: указанная в условии смесь газов имеет плотность 0.47 кг/м3. Задача 8. Вычислить удельные теплоемкости CV и СР смеси неона и водорода, если массовая доля неона w1= 80%, массовая доля водорода w2= 20%. Решение. Удельные теплоемкости идеальных газов выражаются формулами: СV= Где i- число степеней свободы молекулы газа, а m -молярная масса. Для неона (одноатомный газ) i =3 и m =20×10-3 кг/моль, тогда СV1= Для водорода (двухатомный газ) i =5 и m =2×10-3 кг/моль, тогда СV2= Удельную теплоемкость смеси при постоянном объеме CV найдем следующим образом. Теплоту, необходимую для нагревания смеси на D Т, выразим двумя способами: Q=CV×(m1+m2)× D T, Q=(CV1×m1+CV2×m2)× D T, Где CV1 – удельная теплоемкость неона; CV1 – удельная теплоемкость водорода. Приравняв правые части и разделив обе части полученного равенства на D Т получим: CV×(m1+m2)= CV1×m1+CV2×m2, откуда CV= CV1× Где w1= Подставив в полученную формулу числовые значения величин, найдем: CV= (6.24×102 ×0.8+1.04×104 ×0.2)=2.58×103 Дж/(кг×К) Рассуждая таким же образом получим: CР= CР1×w1+CР2×w2. Подставив в полученную формулу числовые значения величин, найдем: CР= (1.04×103 ×0.8+1.46×104 ×0.2)=3.75×103 Дж/(кг×К). Задача 9. В сосуде емкостью 5 л при нормальных условиях содержится водород. Определить коэффициенты диффузии, теплопроводности и внутреннего трения. Решение. Кинетические коэффициенты рассчитываются по формулам: D= c= h= где <l>- средняя длина свободного пробега молекул; <V> - средняя арифметическая скорость молекул; r - плотность газа; CV - удельная изохорическая теплоемкость газа. Для определения кинетических коэффициентов нужно знать значения всех перечисленных величин. <l>= Тогда: <l>= Эффективный диаметр d определяем по справочнику (для водорода d= 2.2×10-9 м). Вычисляем: <l>= <V>= Из уравнения состояния идеального газа p×V=
СV= Теперь можно вычислить все искомые величины: D= h= c= Задача 10. 1 моль кислорода, находящийся при Т =290 К, адиабатически сжали так, что его давление возросло в 5 раз. Определить температуру газа после сжатия и работу, которая была совершена над газом. Решение. Для определения температуры газа Т2 после сжатия используем уравнение Пуассона: Из объединенного газового закона Делаем подстановку: Где g= Вычислим Т2= 290× Из первого начала термодинамики Q= D U+A следует, что при адиабатическом процессе (Q= 0) работа, совершаемая над газом (А<0), идет на увеличение его внутренней энергии. Изменение внутренней энергии связано с теплоемкостью: Следовательно, и работа будет равна этой величине (-А= D U). Знак «минус» показывает, что работа совершалась над газом. Ответ. При сжатии газа совершена работа, равная 3530 Дж.Конечная температура газа 460 К. Задача 11. Тепловая машина работает по обратимому циклу Карно. Температура нагревателя Т1= 500 К. Определить термический к.п.д. цикла и температуру Т2 охладителя тепловой машины, если за счет каждого килоджоуля теплоты, полученной от нагревателя, машина совершает работу А =350 Дж. Решение. Термический к.п.д. тепловой машины показывает, какая доля теплоты, полученной от нагревателя, превращается в механическую работу. Термический к.п.д. выражается формулой h=А/Q1, где Q1- теплота, полученная от нагревателя; А - работа, совершенная рабочим телом тепловой машины. Подставив числовые значения в эту формулу, получим: Зная к.п.д. цикла можно по формуле Т2=Т1×(1-h). Подставив в эту формулу полученное значение к.п.д. и температуры нагревателя Т1, получим: Т2= 500×(1-0.35)=325 К.
КОНТРОЛЬНАЯ РАБОТА № 1. МЕХАНИКА 1.1. Точка обращается по окружности радиусом R =1.2 м. Уравнение движения точки j= А × t +B× t 3, где А =0,5 рад/с; В =0,2 рад/с3. Определить тангенциальное аt, нормальное аn и полное ускорение точки в момент времени t =4 с. 1.2. Точка обращается по окружности радиусом R =2 cм. Зависимость пути от времени дается уравнением х =С× t 3, где С =0,1 см/с3. Определить тангенциальное аt, нормальное аn и полное ускорение точки в момент когда линейная скорость точки равна v =0.3 м/с. 1.3. Точка обращается по окружности так, что зависимость пути от времени дается уравнением х=А + В × t + С × t 2, где где В = -2 м/с; С =1 м/с2. Найти линейную скорость точки, её тангенциальное аt, нормальное аn и полное ускорение через 3 сек после начала движения, если известно, что нормальное ускорение точки при t =2 сек равно аn =0.5 м/с2. 1.4. Найти угловое ускорение колеса, если известно, что через 2 сек после начала равноускоренного движения вектор полного ускорения точки, лежащей на ободе составляет угол 60° с направлением линейной скорости этой точки. 1.5. Определить скорость V и полное ускорение а точки в момент времени t =2 с, если она движется по окружности радиусом R = 1 м согласно уравнению x= А × t + B × t 3, где А =8 м/с; В =-1 м/с3; x- криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности. 1.6. По прямой линии движутся две материальные точки согласно уравнениям: х1= А 1+ В 1× t + С 1× t 2 и х2= А 2+ В 2× t + С 2× t 2, где А 1=10 м; В 1= 1 м/с; С 1=-2 м/с2; где А 2=3 м; В 2= 2 м/с; С 2=0.2 м/с2. В какой момент времени t скорости этих точек одинаковы? Найти ускорения а1 и а2 этих точек в момент t =3 с. 1.7. Определить полное ускорение а в момент t=3 с точки, находящейся на ободе колеса радиусом R=0.5 м, вращающегося согласно уравнению j= А × t + B × t 3, где А =2 рад/с; В =0,2 рад/с3. 1.8. Точка обращается по окружности радиусом R = 8м. В некоторый момент времени нормальное ускорение точки аn =4 м/с2, вектор полного ускорения ` а образует в этот момент с вектором нормального ускорения ` аn угол a =60°. Найти скорость V и тангенциальное ускорение аt точки. 1.9. Точка движется по прямой согласно уравнению х= А × t + B × t 3, где А =6 м/с; В =-0,125 м/с3. Определить среднюю путевую скорость < V > точки в интервале времени от t1 =2 с до t2 =6 c. 1.10. Зависимость пройденного телом пути s от времени дается уравнением s = А+В × t + С × t 2, где А =3 м/с; В =2 м/с; С =1 м/с2. Найти среднюю скорость и среднее ускорение тела за первую, вторую и третью секунды его движения. 1.11. Материальная точка движется прямолинейно. Уравнение движения имеет вид х= А × t + B × t 3, где А =3 м/с; В =0,06 м/с3. Найти скорость v и ускорение а точки в моменты времени t1 =0 с и t2 =3 c. Каковы средние значения скорости < Vх > и < ах > за первые 3 с движения? 1.12. Первую половину времени тело движется со скоростью v1 =20 м/с под углом a1 =60° к заданному направлению, а вторую половину времени – под углом a2= 120° к тому же направлению со скоростью v2 =40 м/с. Найти среднюю скорость движения vср. 1.13. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением j = А+В × t + С × t 2 +D × t 3, где В =1 рад/с; С =1 рад/с2; D =0,1 рад/с3. Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса равно аn =3.46×102 м/с2. 1.14. Колесо вращается с постоянным угловым ускорением e =2 рад/с2. Через 0.5 сек после начала движения полное ускорение колеса стало равно а =13.6 см/с2. Найти радиус колеса. 1.15. Диск радиусом R =0.2 м вращается согласно уравнению j= А+В × t + С × t 3, где А =3 рад; В =-1 рад/с; С =0,1 рад/с3. Определить тангенциальное аt, нормальное аn и полное а ускорение точек на окружности диска для момента времени t =10с. 1.16. Найти во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося колеса, больше её тангенциального ускорения для того момента, когда вектор полного ускорения этой точки составляет угол 30° с вектором её линейной скорости. 1.17. Точка движется по окружности радиусом R =20 см с постоянным тангенциальным ускорением аt= 5 см/с2. Через сколько времени после начала движения нормальное ускорение точки будет: 1)равно тангенциальному; 2) вдвое больше тангенциального? 1.18. Точка движется по окружности радиусом R =10 см с постоянным тангенциальным ускорением аt . Найти нормальное ускорение точки через 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна v =10 см/с. 1.19. Ось с двумя дисками, расположенными на расстоянии l =0.5 м друг от друга, вращается с угловой скоростью, соответствующей частоте n =1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия на первом диске на угол j =12°. Найти скорость пули. 1.20. Камень бросили вертикально вверх на высоту 10 м. 1)Через какое время он упадет на землю? 2)На какую высоту поднимется камень, если начальную скорость камня увеличить вдвое? Сопротивление воздуха не учитывать. 1.21. Свободно падающее тело в последнюю секунду своего падения проходит половину всего пути. Найти: 1) с какой высоты падает тело, 2) продолжительность всего падения. Сопротивление воздуха не учитывать. 1.22. Тело падает вертикально с высоты 20 м с нулевой начальной скоростью. За какое время тело пройдет: 1) первый метр своего пути, 2) последний метр своего пути. Сопротивление воздуха не учитывать. 1.23. Тело падает вертикально с высоты 20 м с нулевой начальной скоростью. Какой путь тело пройдет: 1) за первую 0.1 с своего движения, 2) за последнюю 0.1 с своего движения. Сопротивление воздуха не учитывать. 1.24. С башни высотой Н =25 м бросили камень со скоростью v0 =15 м/с под углом a =30° к горизонту. Найти: 1)сколько времени камень будет в движении; 2)на каком расстоянии от основания башни он упадет; 3)с какой скоростью он упадет; 4) какой угол j составит траектория камня с горизонтом в точке его падения на землю. Сопротивление воздуха не учитывать. 1.25. Тело брошено со скоростью v0 =14.7 м/с под углом a =30° к горизонту. Найти нормальное и тангенциальное ускорение тела через 1.25 с после начала движения. Сопротивление воздуха не учитывать. 1.26. Тело брошено со скоростью v0 =10 м/с под углом a =45° к горизонту. Найти радиус кривизны траектории тела через 1 с после начала движения. Сопротивление воздуха не учитывать. 1.27. Тело брошено со скоростью v0 под углом a к горизонту. Найти величины v0 и a, если известно, что наибольшая высота подъема тела h =3 м и радиус кривизны траектории тела в верхней точке траектории R =3 м. Сопротивление воздуха не учитывать. 1.28. Камень, брошенный со скоростью v0 =12 м/с под углом a =45° к горизонту, упал на землю на расстоянии х от места бросания. С какой высоты h надо бросить камень в горизонтальном направлении, чтобы при той же начальной скорости v0 он упал на то же место? Сопротивление воздуха не учитывать. 1.29. С высоты h =2 м на стальную плиту свободно падает шарик массой m =200 г и подпрыгивает на высоту h1 =0,5 м. Определить импульс ` р, полученный шариком при ударе. 1.30. Молекула массой т =4.65×10-26 кг, летящая нормально к стенке сосуда со скоростью v =600 м/с ударяется о стенку и упруго отскакивает от нее без потери скорости. Найти импульс силы, полученный стенкой за время удара. 1.31. Молекула массой т =4.65×10-26 кг, летящая со скоростью v =600 м/с ударяется о стенку сосуда под углом 60° к нормали и под таким же углом упруго отскакивает от нее без потери скорости. Найти импульс силы, полученный стенкой за время удара. 1.32. К потолку трамвайного вагона подвешен на нити шар. Вагон тормозится и его скорость равномерно изменяется за время D t =3 с от v1 =18 км/ч до v2 =6 км/ч. На какой угол a отклонится при этом нить с шаром? 1.33. Железнодорожный вагон тормозится и его скорость равномерно изменяется за время D t =3.3 с от v1 =47.5 км/ч до v2 =30 км/ч. При каком предельном значении коэффициента трения между чемоданом и полкой чемодан при торможении начнет скользить по полке?
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.178.240 (0.171 с.) |
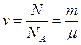 ,
,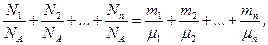
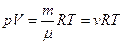
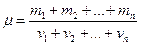 , где тi - масса i -го компонента смеси; vi=mi/mi- количество вещества i -го компонента смеси; n - число компонентов смеси.
, где тi - масса i -го компонента смеси; vi=mi/mi- количество вещества i -го компонента смеси; n - число компонентов смеси.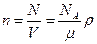 ,
,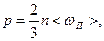
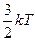 ,
,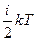 , где i - число степеней свободы.
, где i - число степеней свободы.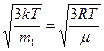
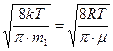
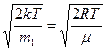 , где т1- масса одной молекулы.
, где т1- масса одной молекулы.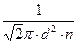 , где эффективный диаметр d определяем по справочнику.
, где эффективный диаметр d определяем по справочнику.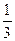 <l>×<V>
<l>×<V> ; СР=
; СР= 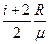 ;
;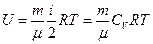
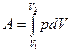 ;
;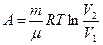 ;
;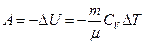 или
или 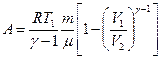 ,
,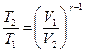 ;
; 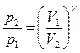 ;
; 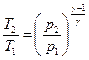
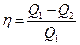 , где Q1 - теплота, полученная рабочим телом от нагревателя; Q2 - теплота, переданная рабочим телом охладителю.
, где Q1 - теплота, полученная рабочим телом от нагревателя; Q2 - теплота, переданная рабочим телом охладителю.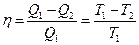 , где Т1 и Т2 термодинамические температуры нагревателя и охладителя.
, где Т1 и Т2 термодинамические температуры нагревателя и охладителя.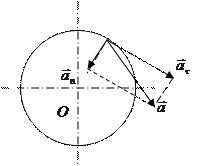 Решение: Полное ускорение ` а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения ` аt, направленного по касательной к траектории, и нормального ускорения ` аn, направленного к центру кривизны траектории (рис 1): ` а =` аt +` аn.
Решение: Полное ускорение ` а точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения ` аt, направленного по касательной к траектории, и нормального ускорения ` аn, направленного к центру кривизны траектории (рис 1): ` а =` аt +` аn. .
.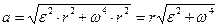
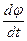 = В +2× С × t, или в момент времени t =4 с угловая скорость:
= В +2× С × t, или в момент времени t =4 с угловая скорость: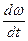 =2С=-4 рад/с2.
=2С=-4 рад/с2.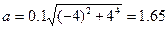 м/с2.
м/с2.
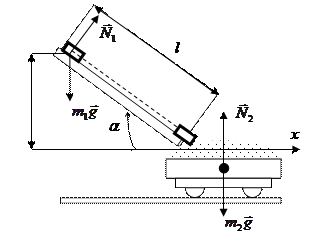 Задача 2. Ящик массой m1 =20 кг соскальзывает по идеально гладкому лотку длиной l =2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2 =80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость u тележки с ящиком, если лоток наклонен под углом a =30° к рельсам.
Задача 2. Ящик массой m1 =20 кг соскальзывает по идеально гладкому лотку длиной l =2 м на неподвижную тележку с песком и застревает в нем. Тележка с песком массой m2 =80 кг может свободно (без трения) перемещаться по рельсам в горизонтальном направлении. Определить скорость u тележки с ящиком, если лоток наклонен под углом a =30° к рельсам. , где р1х и р2х- проекцииимпульса ящика и тележки с песком в момент падения ящика на тележку; а
, где р1х и р2х- проекцииимпульса ящика и тележки с песком в момент падения ящика на тележку; а  -те же величины после падения ящика.
-те же величины после падения ящика.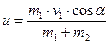
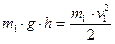 , где h = l×sina.. После сокращений на m1 найдем:
, где h = l×sina.. После сокращений на m1 найдем: 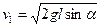 .
.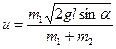 cosa
cosa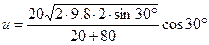 =0.767 м/с
=0.767 м/с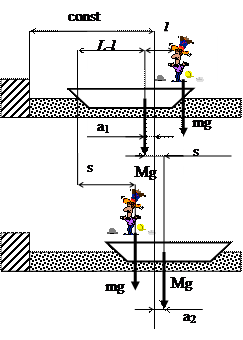 Следовательно, искомое перемещение лодки: S = a1 + a2.
Следовательно, искомое перемещение лодки: S = a1 + a2.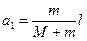 .
. .
.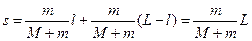 .
.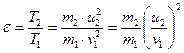 , где Т1 - кинетическая энергия первого шара до удара; u2 и Т2 - скорость и кинетическая энергия второго шара после удара.
, где Т1 - кинетическая энергия первого шара до удара; u2 и Т2 - скорость и кинетическая энергия второго шара после удара. .
. .
.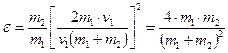 .
. ности и на блок. На первый груз действуют две силы: сила тяжести m1`g и сила упругости (сила натяжения нити) `Т1. Спроектируем эти силы на ось х, которую направляем вертикально вниз, и напишем уравнение движения (второй закон Ньютона) в координатной форме:
ности и на блок. На первый груз действуют две силы: сила тяжести m1`g и сила упругости (сила натяжения нити) `Т1. Спроектируем эти силы на ось х, которую направляем вертикально вниз, и напишем уравнение движения (второй закон Ньютона) в координатной форме: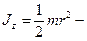 момент инерции блока (сплошного диска) относительно оси z.
момент инерции блока (сплошного диска) относительно оси z.
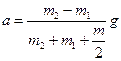 .
.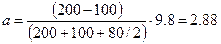 м/с2.
м/с2.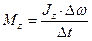 .
.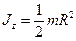 .
.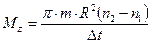 .
.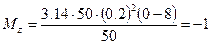 Н/м.
Н/м. , где т - масса смеси. Очевидно, что т=т1+т2.
, где т - масса смеси. Очевидно, что т=т1+т2. +
+  , где v1, т1 - число молей и масса водорода, а v2, т2 - число молей и масса азота.
, где v1, т1 - число молей и масса водорода, а v2, т2 - число молей и масса азота.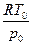 . Отсюда
. Отсюда 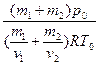 .
.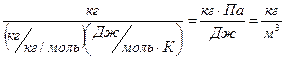
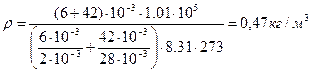
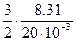 =6.24×102 Дж/(кг×К), а СР1=
=6.24×102 Дж/(кг×К), а СР1= 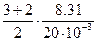 =1.04×103 Дж/(кг×К),
=1.04×103 Дж/(кг×К),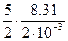 =1.04×104 Дж/(кг×К), а СР2=
=1.04×104 Дж/(кг×К), а СР2= 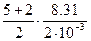 =1.46×104 Дж/(кг×К),
=1.46×104 Дж/(кг×К), +CV2×
+CV2×  или CV= CV1×w1+CV2×w2,
или CV= CV1×w1+CV2×w2, .
.
 » 1,73×10-7 м.
» 1,73×10-7 м. » 1700 м/с.
» 1700 м/с.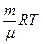 , отсюда
, отсюда » 8,9×10-2 кг/м3.
» 8,9×10-2 кг/м3. .
. получим:
получим:  .
. или
или 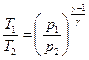 , откуда
, откуда 
 - коэффициент Пуассона (показатель адиабаты); i - число степеней свободы молекул. Для кислорода (двухатомный газ) i= 5, т.е. g= 1.4.
- коэффициент Пуассона (показатель адиабаты); i - число степеней свободы молекул. Для кислорода (двухатомный газ) i= 5, т.е. g= 1.4. »460 К.
»460 К. Дж.
Дж. .
. определить температуру охладителя Т2:
определить температуру охладителя Т2:


