
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описать что такое побитные операции.Содержание книги Поиск на нашем сайте
Описать что такое побитные операции. Лекция 2: Двоичная и шестнадцатеричная арифметика. Представление чисел. Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика, которой мы пользуемся, также называется десятичной. Это потому, что каждое число можно составить из набора цифр содержащего 10 символов - цифр - "0123456789". Но десятичная арифметика не единственная. В областях знаний связанных с компьютерной техникой часто используют арифметику, в которой числа составляются из шестнадцати цифр, соответственно эта арифметика называется шестнадцатеричной. Чтобы понять, что такое число в не десятичной арифметике сначала выясним, что такое число в десятичной арифметике. Возьмём, к примеру, число 246. Эта запись означает, что в числе две сотни, четыре десятка и шесть единиц. Следовательно, можно записать следующее равенство: 246 = 200 + 40 + 6 = 2 * 102 + 4 * 101 + 6 * 100 Наиболее интересна нам сейчас третья форма записи: 2 * 102 + 4 * 101 + 6 * 100. Она устроена следующим образом: В нашем числе три цифры. Старшая цифра "2" имеет номер 3. Она умножается на 10 во второй степени. Следующая цифра "4" имеет порядковый номер 2 и умножается на 10 в первой. Цифра 6 умножается на 10 в нулевой степени. Как можно видеть из примера, каждая цифра умножается на 10 в степени i-1, где i – номер положения этой цифры в числе. Или, записывая в общем виде: anan-1….a2a1 = an * 10n-1 + an-1 * 10n-2 + …. + a2 * 101 + a1 * 100 Где n – количество цифр в числе, ai это символ из набора "0123456789" Десятка является основой образования числа. Если 10 заменить на 2, то получим:
anan-1….a2a1 = an * 2n-1 + an-1 * 2n-2 + …. + a2 * 21 + a1 * 20
где ai это символ из набора "01".
Если а=16, то выражение получает следующий вид:
anan-1….a2a1 = an * 16n-1 + an-1 * 16n-2 + …. + a2 * 161 + a1 * 160 где для обозначения цифр от 0 до 9 используются арабские цифры, а для обозначения цифр от 10 до 15 используются латинские буквы от A до F. В итоге получаем, что 16-тиричная система соотносится с двоичной и 10-ной следующим образом:
При написании чисел в различных системах, необходимо отмечать в какой системе они написаны. Это можно сделать разными способами. К примеру, в Си, если число записано без каких-либо дополнительных знаков, то оно считается десятичным. Прибавление к числу в начале знаков “0x” означает, что число записано в 16-тиричной форме. Например: 0xAB – это запись в 16-тиричном виде десятичного числа 171. Для записи чисел в двоичном виде используется комбинация “0b”. Т.е. десятичное число 123 будет выглядеть так: 0b1111011.
Перевод чисел из одной системы в другую. Перевод двоичных чисел. Возьмём, к примеру, следующее двоичное число 1011. Разложим его по степеням двойки. Получим следующее: 1011 = 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 Выполнив все записанные действия, получим: 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 = 8 + 0+ 2 + 1 = 11.
Следовательно, двоичное число 1011 равно 11 в десятичной системе. Отметим, что в двоичном представлении число имеет большее число разрядов, чем в десятичном. Перевод 16-тиричных чисел.
Эти числа можно перевести двумя способами. 1) Так же как и прошлый раз представить число в виде суммы: anan-1….a2a1 = an * 16n-1 + an-1 * 16n-2 + …. + a2 * 161 + a1 * 160 2) Представить 16-тиричное число в двоичном виде, а затем только перевести его в 10-й вид.
Разберём второй способ подробнее. При переводе 16-тиричного числа в 2-е каждую 16-тиричную цифру заменяют соответствующей ей 2-й комбинацией из 4-х цифр. Например, необходимо перевести уже рассмотренное выше число 0xAB в двоичный код. “А” соответствует в двоичном виде число 0b1010 (см. таблицу 1), а число “B” – 0b1011. В итоге получаем 0b10101011. Перевод десятичного число в двоичное. Для того, чтобы преобразовать десятичное число в двоичное, его нужно разложить по степеням двойки. Преобразование в двоичную систему производится следующим методом: Если число не делится на 2, то отнимают двойку и в двоичное число пишут 1. Если же делится, то ничего не отнимают и записывают ноль. Возьмём десятичное число 23. 23/2=11+1 11/2=5+1 5/2=2+1 2/2=1+0 1/2=0+1 Наше искомое двоичное число 10111. Двоичная арифметика. Сложение двоичных чисел. То есть, сложение выполняется поразрядно, начиная с младшей цифры. Если при сложении двух цифр получается СУММА больше девяти, то записывается цифра=СУММА- 10, а ЦЕЛАЯ ЧАСТЬ (СУММА /10), добавляется в старшему разряду. Так и с двоичным числом. Складываем поразрядно, начиная с младшей цифры. Если получается больше 1, то записывается 0 и 1 добавляется к старшему разряду. Сумму можно описать логической таблицей (см. таблицу 2)
Выполним пример: 10011 + 10001.
010011=19 010001=17 ------------- 100100=36
Вычитание двух чисел. Вычитание двух чисел заменяется сложением уменьшаемого и вычитаемого, представленного в дополнительном коде.
Дизъюнкция В программировании дизъюнкция обозначается обычно как '||' или «OR», читается как 'ИЛИ'. Вот таблица истинности для дизъюнкции:
Дизъюнкция также называется логическим сложением. С тем условием, что 1 AND 1 = 1. Таблица истинности для дизъюнкции в случае замены FALSE на 0, а TRUE на 1 представлена в таблице 5.
Равносильность Обозначается обычно как '==' (двойной знак равно) (см. таблицу 6). Вот его таблица истинности:
Если два значения равны, то условие верно, если не равны, то ложно.
Отрицание Отрицание является унарной операцией, т.е. выполняется с одним операндом. Обозначается как знак '!'. Таблица истинности представлена в таблице 7:
Читается как 'НЕ'. Т.е. (!TRUE = FALSE) Сложение по модулю 2 Последней важной функцией является сложение по модулю 2. Ещё эта функция называется «исключающее ИЛИ». Обычно эта операция обозначается как «^» или «XOR». Её таблица истинности представлена в таблице 8
Таблица истинности в которой FALSE заменено на 0, а TRUE на 1, представлена в табл 9.
А как и следует из названия, эта операция представляет собой сложение по модулю 2. Т.е. 1+1=2. Если взять по модулю 2 (остаток от деления на 2), то выражение 1+1=0.
Смещение двоичных чисел.
Если представить двоичное число как регистр смещения, то мы можем смещать имеющиеся там значения вправо или влево. При этом если сместить число влево на N разрядов, то его значение увеличится в 2N раз. При смещении вправо на N разрядов, значение уменьшается в 2N раз. Т.о. можно легко производить деление и умножение на числа, равные степени двойки. Здесь стоит помнить. Что все биты, выходящие при смещении за разрядность, будут потеряны. Например, возьмём число 0b110011. Сместим его на 3 разряда вправо. 0b000110. И теперь обратно на 3 разряда влево: 0b110000. Аналогично, если у вас разрядность числа ограничена 8 битами (1 байт), то при смещении влево могут быть потеряны старшие разряды. Например, возьмём тоже число 0b110011 и сместим его на 3 разряда влево. Получим 0b011000. Смещая обратно, получим: 0b000110. Как видите, в обоих случаях мы потеряли значащие биты.
Карты Карно. Принципы минимизации Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов. Исходной информацией для работы с картой Карно является таблица истинности минимизируемой функции. Таблица истинности содержит полную информацию о логической функции, задавая её значения на всех возможных 2N наборах входных переменных X1... XN. Карта Карно также содержит 2N клеток, каждая из которых ассоциируется с уникальным набором входных переменных X1... XN. Значения переменных расположены так, что бы менялась только одна переменная. Идея состоит в том, что если от изменения переменной не зависит значение функции, то она не используется. На рис 4. представлено преобразование таблицы истинности в карту Карно.
Рис 4.
Таким образом, между таблицей истинности и картой Карно имеется взаимно однозначное соответствие, и карту Карно можно считать соответствующим образом отформатированной таблицей истинности. Принципы склейки Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить ДНФ (см. рис 5)) или по нулям (если требуется КНФ (см. рис 6)).
Склеивание. Склеивать можно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число. Для карт Карно с числом переменных более четырёх могут получаться более сложные области, о чём будет сказано ниже. Область, которая подвергается склейке, должна содержать только единицы (нули). Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой (топологически карта Карно для четырёх переменных представляет собой тор) и могут объединяться в прямоугольники. Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули) они могут быть объединены в квадрат, как показано на рис. 5. Все единицы (нули) должны попасть в какую-либо область. С точки зрения минимальности ДНФ (КНФ) число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм. Терм размером 2n ячеек содержит N–n переменных). Одна ячейка карты Карно может входить сразу в несколько областей. Это следует из очевидного свойства булевых функций: повторение уже существующего слагаемого (сомножителя) не влияет на функцию:
В отличие от СДНФ (СКНФ), ДНФ (КНФ) не единственны. Возможно несколько эквивалентных друг другу ДНФ (КНФ), которые соответствуют разным способам покрытия карты Карно прямоугольными областями. Построение по картам Карно СДНФ и/или СКНФ. Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути, Карта Карно — это таблица истинности, составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.е. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации. Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки, которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ): 1. Объединяем смежные клетки, содержащие единицы, в область так, чтобы одна область содержала 2. Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки); 3. Несмежные области, расположенные симметрично оси(ей), могут объединяться в одну; 4. Область должна быть как можно больше, а количество областей как можно меньше; 5. Области могут пересекаться; 6. Возможно несколько вариантов покрытия. Далее берём первую область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Составили карту Карно, заполнили области. Наши области перекрыли все имеющиеся в наличии единицы и имеют максимальный размер при наименьшем количестве, т.е. все условия выполнены. Запишем получившуюся функцию. Сначала красная область. Тут изменяется только одна переменная X3. Значит, она не будет участвовать в создании функции для этой области: f1=X1&X2&X4 Аналогично для зелёной и синей. f2=(~X1)&(~X4) f3=(~X2)&(~X4) Итого: f0= X1&X2&X4 | (~X1)&(~X4) | (~X2)&(~X4) Как можно видеть, получившаяся функция не зависит от X3.
Карты Карно от функции пяти и более переменных. Карты Карно в классическом виде хорошо работают только для функций с количеством переменных не более четырёх. При большем количестве переменных появляются дополнительные оси симметричности, что усложняет построение минимальной функции. Для функции пяти переменных можно найти выход, если построить 2 карты Карно, приняв одну из переменных сначала за 0, а потом за 1 и наложив их одну на другую. По получившейся трёхмерной карте можно построить минимальную функцию. Блок-схемы. При блок-схемном описании алгоритм изображается геометрическими фигурами (блоками), связанными по управлению линиями (направлениями потока) со стрелками. В блоках записывается последовательность действий. Данный способ по сравнению с другими способами записи алгоритма имеет ряд преимуществ. Он наиболее нагляден: каждая операция вычислительного процесса изображается отдельной геометрической фигурой. Кроме того, графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали. Оформление программ должно соответствовать определенным требованиям. В настоящее время действует единая система программной документации (ЕСПД), которая устанавливает правила разработки, оформления программ и программной документации. В ЕСПД определены и правила оформления блок-схем алгоритмов (ГОСТ 10.002-80 ЕСПД, ГОСТ 10.003-80 ЕСПД). Операции обработки данных и носители информации изображаются на схеме соответствующими блоками. Большая часть блоков по построению условно вписана в прямоугольник со сторонами а и b. Минимальное значение а равно 10 мм, увеличение а производится на число, кратное 5 мм. Размер b=1,5 мм. Для отдельных блоков допускается соотношение между а и b, равное 1:2. В пределах одной схемы рекомендуется изображать блоки одинаковых размеров. Все блоки нумеруются. Виды и назначение основных блоков приведены в таблице. Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки. Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз. В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков. Из блока (кроме логического) может выходить только одна линия. Логический блок может иметь в качестве продолжения одни из двух блоков, и из него выходят две линии. Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить. Схему алгоритма следует выполнять как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки. Если при обрыве линии продолжение схемы находится на этом же листе, то на одном и другом конце линии изображается специальный символ соединитель — окружность диаметром 0,5 мм. Внутри парных окружностей указывается один и тот же идентификатор. В качестве идентификатора, как правило, используется порядковый номер блока, к которому направлена соединительная линия. Если схема занимает более одного листа, то в случае разрыва линии вместо окружности используется межстраничный соединитель. Внутри каждого соединителя указывается адрес — откуда и куда направлена соединительная линия. Адрес записывается в две строки: в первой указывается номер листа, во второй — порядковый номер блока. Блок-схема должна содержать все разветвления, циклы и обращения к подпрограммам, содержащиеся в программе.
Условные обозначения блоков схем алгоритмов
Пример:
Рис 8
Описать что такое побитные операции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.123.10 (0.011 с.) |

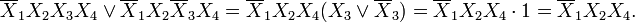





 (
(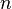 целое число = 0…
целое число = 0…  ) клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули (см рис 5);
) клеток (помним про то, что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток, содержащих нули (см рис 5);













