
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подібність і моделювання в наукових дослідженнях
Методи теорії подібності та моделювання широко застосовуються в різних наукових дослідженнях. Моделювання можна визначити як метод практичної або теоретичної опосередкованої дії з об'єктом. При цьому досліджується не сам об'єкт, а проміжний допоміжний, такий, що знаходиться в деякій об'єктивній відповідності з самим досліджуваним об'єктом і здатний на окремих етапах пізнання представляти в певних відношеннях об'єкт, що вивчається, а також давати на основі дослідження моделі інформацію про об'єкт. При моделюванні важлива та допомога, яку воно надає при виявленні якісних і кількісних властивостей явищ однакової фізичної природи і явищ, різнорідних по своїй фізичній суті. У природі внаслідок її матеріальної єдності є деякі загальні співвідношення і прості форми, що дозволяє робити широкі практичні узагальнення, у ряді випадків відволікаючись в процесі пізнання від деталей явищ, що відбуваються. Таким чином, при моделюванні завжди повинні бути присутніми деякі співвідношення, що встановлюють умови переходу від моделі до досліджуваного об'єкту (оригіналу). Такі співвідношення носять назву масштабів. Моделювання включає наукові дослідження, направлені на вирішення як загальнофілософських і загальнонаукових проблем (перший аспект), так і на вирішення конкретних науково-технічних завдань (другий аспект), де моделювання виступає як інструмент дослідження. Прийоми аналізу і апарат розв’язку при цьому різні, але метод однаково вимагає встановлення критеріїв подібності, тобто словесного або математичного формулювання тих умов, за яких модель може вважатися такою, що закономірно відображає (у тому або іншому сенсі) оригінал. Подібність явищ, що характеризується відповідністю (у окремому випадку пропорційністю) величин, що беруть участь в явищах, що досліджуються, відбуваються в оригіналах і в моделях, за степінню відповідності параметрів моделі і оригіналу може бути трьох видів. Абсолютна подібність, що вимагає повної тотожності станів або явищ в просторі і часі, є абстрактним поняттям, що реалізовується тільки умоглядно. Повна подібність ─ подібність тих процесів, що протікають у часі і просторі, які достатньо повно для цілей даного дослідження визначають явище, що вивчається. Наприклад, можна вважати, що синхронний генератор має повну електромеханічну подібність іншому генератору, якщо всі процеси зміни струмів, напруги, моментів на валу, що його обертають, зміна у часі і просторі розподілу магнітних і електричних полів відрізняються в цих генераторах лише масштабами. При цьому нагрівання або механічна напруга в окремих деталях генератора можуть бути неподібними, оскільки вони не виявляють істотного впливу на електромеханічні явища, що підлягають дослідженню. Проте вони можуть бути найбільш істотними при дослідженні тепломеханічних процесів і т. д.
Неповна подібність пов'язана з вивченням процесів тільки у часі або тільки у просторі. Так, електромеханічні процеси в синхронному генераторі можуть бути подібні у часі без дотримання геометричної подібності полів у середині машини. Наближена подібність реалізується при деяких спрощуючих допущеннях, що приводять до спотворень, які заздалегідь оцінюються кількісно. З точки зору адекватності фізичної природи моделі і оригіналу моделювання може бути фізичне, здійснюване при однаковій фізичній природі явищ, що вивчаються; аналогове, таке, що вимагає відповідності параметрів процесів, що порівнюються, в тому або іншому сенсі. Наприклад, однакової форми рівняння, що описують фізично різнорідні явища: математичне, таке, що передбачає формальні перетворення рівнянь, що полегшують їх розв’язок. Так, якщо диференціальне рівняння (А), що описує фізичний процес, перетворене в рівняння (В), то, встановивши відповідні функціональні зв'язки, можна розглядати А і В як подібні процеси. Умови нелінійної подібності можуть бути знайдені для систем, параметри яких по різному залежать від параметрів режиму. Теореми про подібність. Всі перераховані вище види подібності задовольняють деяким загальним закономірностям, які прийнято називати теоремами про подібність. Цих теорем три. Перша і друга отримані, виходячи з припущення, що мова йде про явища, подібність яких заздалегідь відома. Вони встановлюють співвідношення між параметрами явно подібних явищ, не вказуючи способів визначення подібності між явищами і шляхів реалізації подібності при побудові моделей. Відповідь на останнє питання дає третя теорема. Вона визначає умови, необхідні і достатні для того, щоб явища виявилися подібними.
Перша теорема подібності. У явищ, подібних в тому або іншому сенсі (фізично, математично і т. д.), можна знайти певні поєднання параметрів, які називають критеріями подібності, що мають однакові (чисельно або за функціональними проявми) значення. Слід відмітити, що вірним є і обнонене положення: якщо критерії подібності чисельно однакові, то явища подібні. Розглянемо різні застосування першої теореми: випадок подібних процесів, що описуються однорідними рівняннями
де
де idem означає «відповідно однаково для всіх процесів, що розглядаються»; Критерії подібності будь-якого явища можуть перетворюватися в критерії іншої форми за допомогою операцій множення або ділення раніше знайдених критеріїв один на одного. Так, якщо які-небудь критерії Якщо рівняння процесу характеризують його протікання у часі і просторі з доступною і необхідною для даного дослідження повнотою, то в цьому випадку умови (7.2) ─ критерії повної подібності. Якщо рівняння характеризують протікання процесу або тільки у часі, або тільки у просторі, то (7.2) ─ критерії неповної подібності. Нарешті, якщо початкові рівняння перед визначенням критеріїв будуть спрощені, в них будуть відкинуті якісь явно впливаючі фактори і т. д., то знайдені з них критерії (7.2) називатимуться критеріями наближеної подібності. У табл. 7.1...7.3 наведені критерії подібності для деяких найбільш характерних процесів. У випадку подібних процесів, що описуються рівняннями з неоднорідними функціями (трансцендентні, складні і т. д.), аргументи неоднорідних функцій повинні бути рівні, оскільки вони в цьому випадку є критеріями подібності. Так, наприклад, якщо у функціях Перша теорема про подібність справедлива і в більш складних випадках, коли рівняння процесів на перший погляд неоднакові, але введення змінних масштабів параметрів часу або простору дає можливість встановити відповідність між оригіналом і моделлю. Можливі, наприклад, два випадки подібності: звичайне геометричне, коли куб перетворюється в подібний куб (іншого розміру), і так зване афінне, коли куб перетворюється в паралелепіпед. Можуть реалізовуватися і складніші перетворення, наприклад, коли куля (глобус) зображається у вигляді плоскої моделі (карти); це ─ конформне перетворення. Друга теорема подібності. Всяке повне рівняння фізичного процесу, записане в певній системі одиниць, може бути представлене у вигляді залежності між безрозмірними співвідношеннями парараметрів, що входять у рівняння, які і є критеріями подібності. Таблиця 7.1.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.55.14 (0.007 с.) |
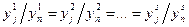 , (7.1)
, (7.1) ─ номери процесу;
─ номери процесу;  ─ параметри відповідно моделі і об'єкту. Індекси, які характеризують номер процесу, можна опустити і записати (7.1) у більш загальному вигляді:
─ параметри відповідно моделі і об'єкту. Індекси, які характеризують номер процесу, можна опустити і записати (7.1) у більш загальному вигляді: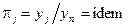 , (7.2)
, (7.2) ─ критерії подібності.
─ критерії подібності. = idem і
= idem і  = idem, то
= idem, то 
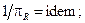
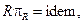 де
де  ─ будь-яка стала величина.
─ будь-яка стала величина. виконується умова
виконується умова  , то подібність процесів характеризується рівністю
, то подібність процесів характеризується рівністю  . Можливі умовно подібні процеси, подібність яких виконується при введенні змінних масштабів (квазіподібність).
. Можливі умовно подібні процеси, подібність яких виконується при введенні змінних масштабів (квазіподібність).


